圏論で使う絵算〈{graphical | pictorial | diagrammatic} {calculation | computation}〉については、次の記事で詳しく説明しています。
上記過去記事にしたがって多少のトレーニングをすれば圏論的絵図の読み・書き〈描き〉・計算が出来るようになると思います。今日のこの記事では、絵算をはじめた人への若干の注意事項を補足することにします。
内容:
図式順演算子記号
「圏論の随伴をちゃんと抑えよう: お絵描き完全解説」では、絵図だけではなくて、次のテキスト記法についても説明しています。
- 関手の結合、関手と自然変換のヒゲ結合、自然変換の横結合を、いずれもアスタリスク〈'*'〉で書く記法
- 自然変換の縦結合を、セミコロン〈';'〉で書く記法
- 対象・射への関手の適用、自然変換の成分を、いずれもドット〈'.'〉で書く記法
- 恒等関手と恒等自然変換をハット〈カレット | サーカムフレックス | '^'〉で書く記法
今出てきた演算子記号は、いずれも図式順演算子記号です。多数派は反図式順なので、対応を表にすると:
| 演算 | 図式順事例 | 反図式順事例 |
|---|---|---|
| 関手結合、ヒゲ結合、横結合 | F*G, F*β, α*β | G・F, β・F, β・α |
| 縦結合 | α;β | β |
| 適用、成分 | A.F, A.α | F(A), αA |
| 恒等関手、恒等自然変換 | F^, α^ | IdF, IDα |
2次元または3次元の絵図的状況を、無理に1次元にシリアライズしている時点でテキスト記法は分かりにくいのですが、さらに方向の逆転が入ると、絵図とテキストとのギャップに苦しむことになります。使う演算子記号を全部図式順にすれば、負担が軽くなります。
僕はそもそもテキスト記法はあんまり使いませんが、使う場合は100%図式順記法です。混乱しがちでストレスフルな反図式順記法を使う理由は何もないからです。ただし、反図式順記法が多数派(いわば標準記法)であるので、コミュニケーション手段として反図式順記法に翻訳することは多々あります。「郷に入っては郷に従え」は守ってます。
特定コミュニティ内のローカルな標準としては、図式順記法を採用することをおすすめします。無意味な混乱とストレスから開放されますから。
描画方向
関手、自然変換、(特別な関手である)モノイド積を扱う状況を考えましょう。このとき、3つの方向が必要です。
| 方向 | その方向の演算 |
|---|---|
| 第一方向 | ; |
| 第二方向 | ., * |
| 第三方向 | ×, |
通常、描画キャンバスは2次元なので、3つの方向から2つを選びます。その2つの方向を主方向と副方向と呼びましょう。主方向/副方向の選択肢は二種です。
| 選択肢番号 | 主方向演算 | 副方向演算 |
|---|---|---|
| 1 | ; | ., * |
| 2 | ; | ×, |
1番は、縦結合と横結合を扱います。2番は、縦結合とモノイド積を扱います。3次元図を描けばすべて同時に扱えますが、3次元図は一般的ではありませんし、描画に手間がかかります。
最後に、2次元の描画キャンバス(紙やホワイトボード)の縦方向と横方向に、主方向と副方向を割り当てる必要があります。主方向の取り方が4種類、それに対して副方向が二種類取れるので8種類の方向の取り方があります。3つの方向から2つの方向を選ぶ方法が2種(選択肢1番と2番)あったので、合計で16種類の描画手法があります。16種のどの方法で描かれているかを見極め解釈するにはそれなりのトレーニングが必要です。
自分で図を描くときは、描画方向を明示したほうが親切です。
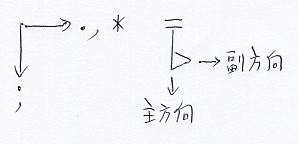
上図の左のような注釈を書いておくと、適用と横結合が左から右、縦結合が上から下だとすぐに分かります。主方向と副方向にどんな演算を選んだかは了解済みなら旗(上図の右)を使って主方向/副方向を示してもかまいません。
格上げと同一視
格上げについては、過去記事の次の節で説明しています。
圏の対象 X in C に対して、関手 X~:☆ → C in CAT が構成できて、圏の射 f:X → Y in C に対しては、自然変換 f~::X~ ⇒ Y~:☆ → C in CAT が構成できます。そして、X~とX、f~とfを同一視します。
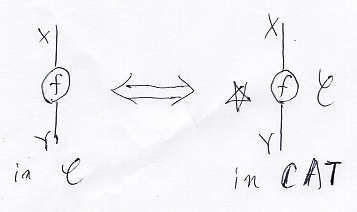
こうすることによって、圏の対象、圏の射、関手、自然変換の4種の圏論的実体を、関手と自然変換の2種だけとして扱うことができます。圏の圏CAT内のストリング図に、圏の対象・射も一緒に描けることになるのです。これは、とんでもないイノベーションで、ストリング図と絵算の利便性が向上し、適用範囲を格段に拡げました。
ノード形状
今話題にしている絵図においては、ノードは自然変換と自然変換で表現される射を表します。ノードの形状は色々あります。例えば、f:X → YZ を表すノードの形状のレパートリは:

他にいくらでもノード〈アイコン〉のデザインは作れます。ノードの形状が何を表すかというと:
- 自然変換・射の種類を、形状や色で表現している。
- 気分や好みで形状や色を選んでいるだけ。
- 使っている描画ツールやレイアウトの都合で形状や色が制限されている。
1番の場合は、前もって「自然変換・射の種類 ←→ 形状や色」の対応ルールが必要です。暗黙のルールや習慣もあります。2番、3番の理由で、ノードの形状・色に特に意味がないときもあるので注意してください。ワイヤーの太さ・色なども同様な事情です。
3次元ビュー
通常の描画キャンバスは2次元ですが、3次元的な状況を思い描いておいたほうがいいことがあります。
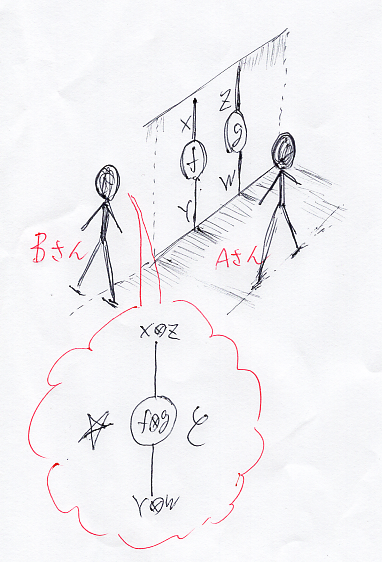
上の絵では、AさんとBさんがいます。Aさんの視点では:
- モノイド積
の方向が左から右
- 自然変換・射の結合 ; の方向が上から下
Bさんの視点では:
- 関手結合・横結合 * の方向が左から右
- 自然変換・射の結合 ; の方向が上から下
Aさんからは、射のモノイド積 (f:X → Y) (g:Z → W) がハッキリと見えています。一方のBさんからは、モノイド積は奥ゆき方向で重なっているので、それほどハッキリは見えません。が、頭を左右にふればモノイド積も認識はできるので、f
g:☆ → C (左から右)という形で状況は見えています。
Aさんの立ち位置は、圏C側の空間で、Bさんの立ち位置は、自明圏☆と圏Cの境い目をまたいでいます。AさんやBさんが空を飛べる(立体起動装置を装備できる)として、3次元的に位置を変えたときに、どのような景色が見えるかを考えてみるのもいいでしょう。
3次元ビューに関しては次の記事も参考になるでしょう。
テキストへの翻訳
コミュニケーションの都合で、絵図をテキストに翻訳する必要が生じます。一例をやってみましょう。
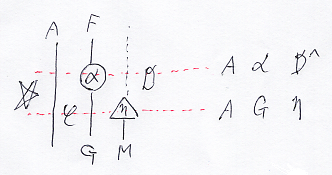
上の図で、目ぼしいノードはαとηなので、これらのノードを横に切る補助線(赤い点線)を引いて、ラベルの2次元的配置を取り出します。この2次元配置〈行列〉に演算子記号を入れて1次元に押し込めて、左右の順番も入れ替えましょう。
最後の結果
[/追記][/補足]
僕自身は、絵でもテキストでも、「左から右、上から下」を標準の〈デフォルトの〉方向と決めて、ほとんどすべてこの方向で描画・書字をしています。どうしても必要があるときだけ翻訳をします。
ウィラートン〈Simon Willerton〉のように、絵でもテキストでも「右から左、下から上」を自分の標準だと決めて、それで統一するのもありでしょう。しかし残念ながら、通常の書字(英語や日本語の書字)の方向とは逆であり、そのギャップは埋まりません。ウィラートン自身が、混乱して間違えている様子をYoutubeビデオで見たことがあります。