「フローチャートを復権させよう -- 2020年代のプログラミングへ」において、プログラムに関係する絵・図の話をしたのですが、僕がフローチャートを使いたい理由(いくつかある)のひとつは、一種のカリー/ハワード対応を利用したいからです。
カリー/ハワード対応とは、論理とプログラムの対応のことです。“連言と含意を持つ論理”と“型付きラムダ計算”の対応が有名ですね。僕がこれから話題にするのは、“古典論理(風)のシーケント計算”と“コマンド言語によるプログラム”の対応です。コマンド言語とは、「コマンド」と呼ばれる処理の基本単位があり、コマンド達をパイプで結合してプログラムを作るスタイルのスクリプト言語です。具体例は、我々(檜山とKuwataさん)が開発しているCatyScriptを想定しています。
シーケント計算とコマンド言語プログラミングの対応を構成するにあたって、中間にフローチャートを挟むと、とても分かりやすくなります。つまり、次のような対応関係を考えることになります。
- シーケント計算 ⇔ フローチャート ⇔ コマンド言語プログラミング
内容:
- シーケントとその図示
- 左右のカンマの解釈が違う
- 命題の列を表す変数
- たばねること、ばらすこと
- 複数のワイヤーを1本に、1本のワイヤーを複数に
- コマンドを絵に描くと
- カリー/ハワード対応
- オマケ:今回使った絵について
- 参考:カリー/ハワード対応 関連記事
- 参考:シーケント計算 関連記事
シーケントとその図示
A, X など英字大文字は命題(構文的には論理式)を表すとします。シーケントとは、A, B, C ⇒ X, Y, Z のように、矢印の左右に命題をカンマで区切って並べた形式です。矢印は、「→」、「⇒」(アスキー文字だけ使うなら「=>」、「==>」)、「|-」などが使われます。今の例では左右とも3つの命題が並んでますが、命題の個数は自由です。
古典論理では、左右に並ぶ命題の個数は自由ですが、直観主義論理では右側には1個の命題か、なにもないかです。命題の個数や、並べ替え/増減などの操作を制限すると、異なった論理体系となります。ここでは、古典論理のシーケント計算体系を採用します。
とりあえず、シーケント A, B, C ⇒ X, Y, Z は次のように図示します。
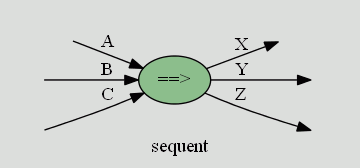
そのまんまですね。
左右のカンマの解釈が違う
シーケント計算では、左側のカンマと右側のカンマの解釈が異なります。左側の A, B, C は、A∧B∧C のように解釈するので、カンマはAND(連言)結合子と解釈します。右側の X, Y, Z の解釈は、X∨Y∨Z と、OR(選言)結合子に解釈します。シーケント全体は、(A∧B∧C)⊃(X∨Y∨Z) という含意命題、あるいはこの命題が成立することを主張する |- [(A∧B∧C)⊃(X∨Y∨Z)] というメタ命題と解釈されます。
図では、ワイヤーが命題で、並んだ命題はワイヤーの束<たば>です。カンマの解釈の違いから、束の解釈も場所により違うことになります。これはかなりヤヤコシイ話で、混乱の原因となります。現実問題としては何らかの対処が必要だと思ってますが、とりあえずは「注意して下さい」で先に進むことにします。
命題の列を表す変数
シーケント計算では、命題の列を Γ, Δ などのギリシャ大文字で表現するのが習慣です。例えば、B, C という列を Γ で表し、Y, Z という列を Δ と置くと、A, B, C ⇒ X, Y, Z は次のように書けます。
- A, Γ ⇒ X, Δ
ギリシャ大文字は、空な列を表すこともあります。Γ が空なら、A, Γ は単に A のことです。
さて、命題の列に対応するワイヤーの束を、太い破線で表して次のように図示することにします。
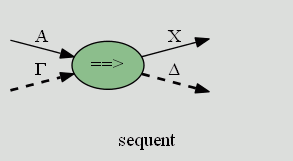
たばねること、ばらすこと
「B, C をまとめて Γ とする」ことを操作と考えて、茶色の菱形で図示することにします。同様に、「Δ をばらして Y, Z とする」ことは白い菱形で表します。そうすると、Γ は A, B で、Δ が Y, Z のときの A, Γ ⇒ X, Δ は次のようになります。
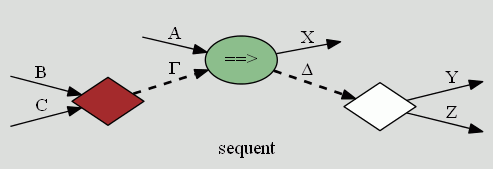
A, A, B ⇒ X, Y, Z と A, Γ ⇒ X, Δ は実質的に何の違いもありません。ワイヤーをグルーピングしたり、グループ(列、束)を解消したりという「見方」を変えているだけです。
複数のワイヤーを1本に、1本のワイヤーを複数に
なんだかバカみたいですが、一見バカみたいで、どうでもよいほどに自明なことが最重要な鍵だったりします。実際、バカみたいなワイヤー操作がシーケント計算のキモなのです。
少しだけ自明でない操作を入れてみます。カンマを取り除いたり挿入したりする操作です。図のうえでは、複数のワイヤーを1本にする、あるいはその逆の操作になります。先ほどのようなグルーピングとは異なります。グルーピング(とグループの解消)ではワイヤーの本数が変わりませんが、これから行う操作ではワイヤーの本数が変化します。次の図を見てください。
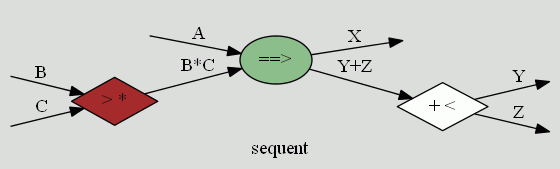
茶色の菱形による作用は次の推論規則に対応しています。論理演算だけでなく、より一般の演算(例えば直積と直和)を想定して、掛け算記号 * と足し算記号 + を使って記述します。
A, B ⇒ Ψ
-------------
A*B ⇒ Ψ
白い菱形を付加することは、次の推論規則に対応しますね。
Φ ⇒ Y+Z
-------------
Φ ⇒ Y, Z
これは場合分けの実行なので、次のように書くほうが分かりやすいかも知れません。縦棒は、ANDではなくてORを意味する仕切りです。
Φ ⇒ Y+Z
----------------------
Φ ⇒ Y | Φ ⇒ Z (2つの場合に分ける)
逆向きだと、選言記号(∨や+)の導入規則です。
Φ ⇒ Y | Φ ⇒ Z (2つのうちのどちらか一方)
---------------------
Φ ⇒ Y, Z
-------------
Φ ⇒ Y+Z
圏と多圏の概念・用語法を使うと、もっとスッキリと記述できます(今日はやりませんが)。
[追記] シーケントと多圏に関する導入的解説は、次のブログ記事がいいと思います。
[/追記]
コマンドを絵に描くと
Catyのコマンドは、コマンドライン・パラメータ(オプション・パラメータと引数パラメータ)と、実行時の文脈から決まる標準入力を受け取ります。コマンドの実行結果は標準出力に書き出すか、または例外を投げます。エラーを意味する例外以外に、正常な大域脱出であるシグナル送出により終了することもあります。例外とシグナルのメカニズムはほとんど同じで、まとめて Throwable*1 と呼んでもいいでしょう。
と、このような事情を絵に描くと次のようになります。
図形としては、シーケントの図示と同じです。コマンドの仕様をシーケントの形で書けば:
- StdIn, Opts, Argv ⇒ StdOut, Exception, Signal
- または、StdIn, ParamVars ⇒ StdOut, Throwable
左右のカンマの意味はどうでしょうか。入力側は直積(タプル)に組まれます。つまり、StdIn×Opts×Argv = StdIn×ParamVars が入力全体の型です。一方、出力側は直和(排他的ユニオン)に組まれ、StdOut + Exception + Signal = StdOut + Throwable が出力全体の型となります。
実行環境の背後には、大量のモナド類似物がいるので、この絵はモナド類似物のクライスリ類似圏のなかで解釈することになりますが、その点は絵に描いてありません。ソフトウェア的な利便性とかの理由で、実際には若干変形した絵を使いますが、基本は今述べたとおりです。
カリー/ハワード対応
シーケント計算、コマンドプログラミング、フローチャート(有向グラフによる可視化)の対応を表にまとめておきます。
| シーケント計算 | コマンドプログラミング | フローチャート |
|---|---|---|
| 命題 | 型 | ワイヤー |
| シーケント | コマンド | ノードと近傍 |
| 推論規則 | プログラムの構成法 | グラフ(絵)の組み立て方 |
| 証明 | プログラム | グラフ(絵) |
| 証明の変形 | 最適化やリファクタリング | グラフ書き換え |
| カット消去手順 | 最適化コンパイラ | グラフの正規化 |
ちなみにジラールの用語法では、プログラムの実行とはコンパイルのことであり、実行結果とは最適化/正規化されたプログラムのことです。正規化されたプログラムをデータとか値と呼ぶのです。一見奇妙ですが、もともとコンパイラとインタプリタの境界は曖昧ですから、計算の実行を思いっきりコンパイルタイムに持ってくれば、コンパイル結果をデータ/値と呼ぶのも「まーいいんじゃないの」と思えます。
オマケ:今回使った絵について
この記事に載せた絵は、例によってGraphvizで描いています。僕にとっては極めて使いやすく、他の人にとってはおそらく使い物にならない*2描画ツール(Graphvizのフロントエンド)をKuwataさんが作ってくれました(ライブラリのバグや変なクセに悩まされながら)。それを使って描いています。コチラで少し紹介しています。
1枚描く手間は手描きよりずっと大変ですが、保存と再利用がとても容易なので、トータルでは効率が上がると思います。第一、キレイに描けるしね。
