次の記事で明瞭正規表現について説明しました。
他に、メモ編にも記述がありますが、自分(檜山)向けメモなので、他の人には分かりにくいでしょう。
この記事で、明瞭正規表現とオートマトンの関係について割とチャント述べます。「割とチャント」なので長いです。
内容:
- 有向グラフの基本を少し
- 扱いやすいオートマトン
- 構成と証明の戦略
- オートマトン/有向グラフの変形
- 明瞭正規表現と扱いやすいオートマトン
- G? の構成
- (G, H) の構成
- (G | H) の構成
- G+ の構成
- Q.E.D.
- 明瞭正規表現の問題点
有向グラフの基本を少し
オートマトンの状態遷移グラフは、辺ラベル付き有向グラフなので、有向グラフの一般論から用語を少し準備しておきます。
基点とか始点と呼ばれる頂点(ノード)を固定した有向グラフを考えます。有向グラフGの基点をiとします。グラフGの頂点xに、基点iから有向辺を順方向にたどって行けるとき、xは可達(reachable)と呼びます。可達でない頂点は不達(unreachable)と呼びます。
経路(path, walk, trajectory)という言葉を使って言えば:
- xは可達 ⇔ 基点iから頂点xに至る経路が存在する
- xは不達 ⇔ 基点iから頂点xに至る経路が存在しない
次の図で、0番のノードが基点iだとして、2番、3番は可達、1番、4番、5番は不達です。
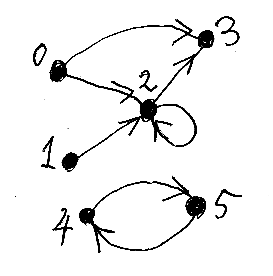
グラフGの頂点xに対して、xに入る有向辺の本数をxの入次数(in-degree)、xから出る有向辺の本数をxの出次数(out-degree)と呼びます。それぞれを、indeg(x)、outdeg(x) と書きましょう*1。次の事実は簡単ですが、不達ノードの判定に使います。
- グラフGの頂点xは基点ではなくて入次数が0 ⇒ xは不達
逆は成立しないので注意してください。それは、すぐ上の例から分かるでしょう。
グラフGが辺ラベル付き有向グラフだとして、頂点xに入る辺のラベルを合併した集合を inLabels(x)、頂点xから出る辺のラベルを合併した集合を outLabels(x) とします。もう少しキチンと定義するために、次の記号を定義します。
- Edge(G) = (Gの辺の集合)
- src(e) = (辺eの始点)
- trg(e) = (辺eの終点)
- A = (辺ラベルの集合)
- label:Edge(G)→A 辺ラベリング関数
- inEdges(x) = {e∈Edge(G) | trg(e) = x}
- outEdges(x) = {e∈Edge(G) | src(e) = x}
以上の記法のもとで:
- inLabels(x) = {a∈A | ∃e∈inEdges(x).(label(e) = a)}
- outLabels(x) = {a∈A | ∃e∈outEdges(x).(label(e) = a)}
つまり、inLabels(x) は、辺ラベリング関数の inEdges(x) に対する像集合、outLabels(x) は、辺ラベリング関数の outEdges(x) に対する像集合です。
集合Xの基数(cardinality)を #(X) とすると:
- #(inLabels(x)) ≦ indeg(x)
- #(outLabels(x)) ≦ outdeg(x)
indeg(x) = #(inEdges(x))、outdeg(x) = #(outEdges(x)) なので当然です。
扱いやすいオートマトン
アルファベットがAである言語の受理オートマトンを考えます。オートマトンの状態遷移グラフをGとします。Gの頂点(ノード)の集合Node(G)は状態空間なのでSとも書きます。初期状態=基点=始点をiとします。終状態の集合をFとします。F⊆S 以外にFに制限はありません。Fが空集合でもかまいません。F = S でもかまいません。
アルファベットAに含まれない記号を、列(語)の終端記号に使います。終端記号(end-of-sequenceマーカー)を$として、A' = A∪{$} としましょう。Aの列(A*の要素)の最後に$を付けた列をオートマトンの入力列とすることにします。Sに含まれないzを取って、S' = S∪{z} とします。f∈F とzのあいだは、$でラベルされた辺で結ぶことにします。
以上にようにして作ったS'を改めてSと置いて、はじめから z∈S であったかのように扱うことにしましょう。i∈S と F⊆S は今までと同じ意味です。
オートマトンが次の条件を満たせば、それはとても扱いやすいモノになります。
- indeg(i) = 0
- zが存在すれば、outdeg(z) = 0 (zが存在しないときもあります*2。)
- zが存在すれば、inLabels(z) = {$}
- indeg(x) = 0 ならば x = i
- outdeg(x) = 0 ならば x = z
- すべての頂点(状態)は、iから可達。
- z以外の任意の頂点xと任意の入力記号a($でもよい)に対して、遷移先の頂点が一意的に決まっている。
このような条件を満たすオートマトンは決定性です。すべての遷移辺に集合A'によるラベルが付いているので、イプシロン遷移(後述)は存在しません。上記条件を満たすオートマトンに特別な名前は付けず、単に扱いやすいオートマトンと呼ぶことにします*3。扱いやすさの条件には実務上の要求も入れているので、理論上はもっとゆるい条件でいいことは注意しておきます。
この記事の目的は、明瞭正規表現が“扱いやすいオートマトン”にコンパル可能なことを示すことです。
構成と証明の戦略
今さっき書いたように、これから「明瞭正規表現が“扱いやすいオートマトン”にコンパル可能なことを示す」ことにします。実装にそのまま使える構成法によりこれを示します。
明瞭正規表現の定義が帰納的(inductive)だったので、証明も帰納的証明(mathematical induction)を使います。帰納的証明はベース(basis)と帰納ステップ(inductive step)から構成されます。今回の場合、ベースの部分は次のようになります。
帰納ステップは、明瞭正規表現の構成法に対応します。そして、構成は演算子(メタ文字、メタ記号)により行われます。正規表現で使う演算子は、'?', ',', '|', '*', '+' などがありますが、これらは独立ではありません。E? = (E | 1)、E* = (1 | E+)、E+ = (E, E*) のような関係があります。どれをプライマリーなものに選ぶかは恣意的だし、気にするほどの問題でもないので、'?', ',', '|', '+' を基本構成法に選んで*4、'*' は E* := (E+)? と後から定義することにします。
そう決めると、帰納ステップは次のようになります。
- 明瞭正規表現 E に対応する言語を受理する“扱いやすいオートマトン”が存在するならば、E? に対応する言語を受理する“扱いやすいオートマトン”も存在する。
- 明瞭正規表現 E, F に対応する言語を受理する“扱いやすいオートマトン”が存在するならば、(E, F) に対応する言語を受理する“扱いやすいオートマトン”も存在する。
- 明瞭正規表現 E, F に対応する言語を受理する“扱いやすいオートマトン”が存在するならば、(E | F) に対応する言語を受理する“扱いやすいオートマトン”も存在する。
- 明瞭正規表現 E に対応する言語を受理する“扱いやすいオートマトン”が存在するならば、E+ に対応する言語を受理する“扱いやすいオートマトン”も存在する。
ただし、明瞭正規表現の場合、構成のときに事前の条件があります。
- E から E? を構成する際には特に条件がない。
- E, F から (E, F) を構成する際には、「FollowLast(E)∩First(F) が空集合」という条件。
- E, F から (E | F) を構成する際には、「First(E)∩First(F) が空集合」という条件。
- E から E+ を構成する際には、「FollowLast(E)∩First(E) が空集合」という条件。
これらの条件により、コンパイルの容易性や実行時の(相対的な)高速性が担保されます。
オートマトン/有向グラフの変形
実際の構成と証明に入る前に、オートマトン/有向グラフの変形について準備しておきます。テクニカルな道具としては、ここで述べる変形のテクニックがキモと言えます。
ここでは、オートマトンと有向グラフをあまり区別しません。つまり、「オートマトン」が状態遷移グラフを意味するかもしれないし、「グラフ」が対応するオートマトンを意味するかもしれません。頂点、ノード、状態は同義語、(ラベル付き)辺と遷移も同義語として扱います。
オートマトン/有向グラフの変形として、次の4つの方法を紹介します*5。
これらの変形操作を行なっても、言語の受理オートマトンとしての機能は変わりません。
辺の集約と集合値ラベル
オートマトンの状態遷移グラフは、ラベル付きのループと多重辺を許す有向グラフです。言語のアルファベットAが、辺ラベルの集合(ラベリング関数の余域)となります。
2つの頂点(ノード)を固定したとき、この2頂点を結ぶ有向辺は何本あっても(0本でも)かまいません。しかし、グラフ描画ツールで実際に絵を描いたり、グラフを行列により表現するときは、多重辺は邪魔です。複数のラベル付き辺を1本にまとめしょう。次の図がその例です。
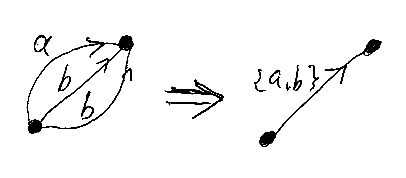
この図では辺が3本ありますが、同じラベルbが付いている辺を2本描いているので冗長(単なる描きすぎ)です。異なるラベル(ここではaとb)を持つ辺は区別されるべきものです。多重辺を集約して1本の辺にしたときには、情報が失われないようにラベルのほうを集合値にします。
3本の辺についていたラベルがそれぞれ a, b, b ならば、集約した1本の辺には {a, b, b} = {a, b} という集合でラベルを付けます。ラベルが集合 {a, b} であることは、「入力がaまたはbならば遷移する」を意味します。
ブラックホールの追加
状態=グラフの頂点がブラックホールであるとは、一度そこに陥ったら抜けられない状態のことです。s∈S がブラックホールであるとは:
- 任意の入力記号($も含める)aに対して、(s, a)|→ s という遷移をする。
状態tと入力aに対して、(t, a) からの遷移が未定義のとき、ブラックホールに遷移させるか、tをブラックホール化することにより「未定義」を取り除くことができます。遷移が未定義とは、ソフトウエア的には例外の発生を意味するので、例外を避けたいときはブラックホール状態を追加することになります。ブラックホールは何個あってもかまいません。例外のほうがむしろ望ましいときは無理にブラックホールにする必要はありません。
不達ノードの除去
不達ノードは取り除いても、オートマトンとしての能力に影響はありません。不達ノードから出る辺も一緒に取り除きます。不達ノードに入る辺があれば、その辺と根本のノードも取り除けます。
イプシロン辺の除去
イプシロン辺とは、ラベルが付いていない辺のことです。何も書いてないと紛らわしいのでギリシャ文字εを添えるのが習慣ですが、「εという実際の記号がラベルとして付いている」のではありません。辺を状態遷移と解釈するときは、入力が何もないのに起きる遷移がイプシロン辺に対応し、イプシロン遷移と呼びます。
今回のケースでは次の仮定を置けます。
この仮定があるとき、イプシロン辺の除去は簡単です。次の図で説明しましょう。
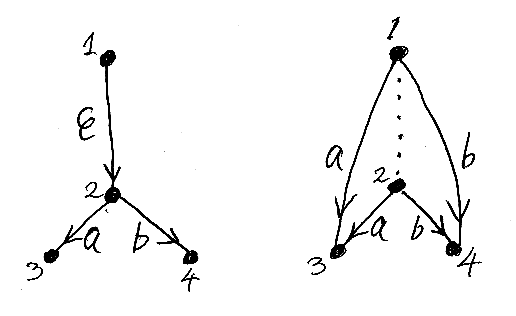
頂点1から頂点2に向かうイプシロン辺があります。頂点2からは、a, b とラベルされた2本の辺が出ています。頂点2から出ている辺と同じ行き先とラベルを持った辺を、頂点1に付け加えます。具体的には、(1, a)|→ 3 と (1, b)|→4 を付け加えました。これらの辺を加えると、イプシロン辺を経由する必要はなくなるので、お払い箱のイプシロン辺を除去できます。
この例では、頂点2に入る辺がなくなるので、イプシロン辺除去により頂点2は不達になり、不達ノード除去の対象になります。
明瞭正規表現と扱いやすいオートマトン
さて、準備も出来たので、「明瞭正規表現が“扱いやすいオートマトン”にコンパイルできる」ことを、数学的帰納法で示しましょう。
帰納法のベースとして、言語の族Bに属する言語(を表す定数記号)は「“扱いやすいオートマトン”にコンパイルできる」必要があります。これは天下りに仮定します。別な言い方をすると、そのようなBを選んでください、ということです。Bとして、長さ1の列からなる単元集合の族を取れば仮定を満たします。
定数記号 0, 1 に対応するオートマトンが扱いやすいことは次の図から分かります。
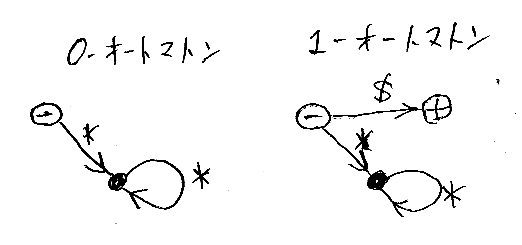
ラベルの星印はワイルドカードで、明示的に書いてないその他すべての入力記号を意味します。この2つのオートマトンで、黒丸のノードはブラックホールになっています。
帰納法のステップを記述するにあたって、オートマトンに対応するグラフGを一般に次のように図示します*6。
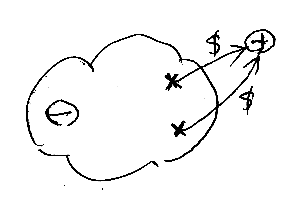
- マイナスのノードは初期状態=入り口です。
- バッテンのノードは終状態です。
- プラスのノードは(終状態とは別に設けた)出口です。
- 終状態から出口への辺は必ず終端記号$でラベルされています。
G? の構成
入り口と出口を、$でラベルされた辺で繋げます。もともと、(入り口, $)|→出口 という辺があれば何もする必要はありません(冗長な辺を描くだけなので)。
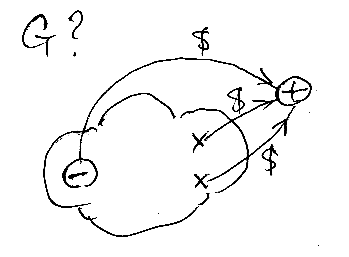
Gが“扱いやすいオートマトン”ならば、この操作をしても“扱いやすいオートマトン”です。
(G, H) の構成
Gの終状態と出口を結ぶ辺をイプシロン辺に変えて($を取り去って)、Gの出口(プラス)とHの入り口(マイナス)を重ねます。
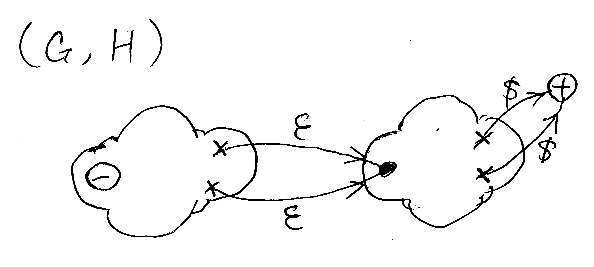
この操作によりイプシロン辺が何本かできるので、すべてのイプシロン辺を除去します。イプシロン辺を除去すると、もともとはHの入り口だったノードは不達ノードになるのでこれも除去します。こうして最終的に出来上がったグラフは“扱いやすいオートマトン”です。
明瞭正規表現の構成に関する「FollowLast(E)∩First(F) が空集合」という条件は、この操作により非決定性が生じないために必要だったのです。
(G | H) の構成
新しい入り口ノードを作って、新しい入り口ともとの2つの入り口をイプシロン辺で繋げます。2つの出口ノードは重ねあわせて1つにします。
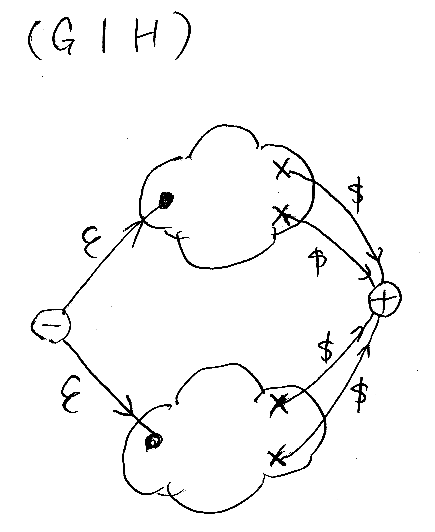
この操作によりイプシロン辺が2本できるので、2本のイプシロン辺を除去します。イプシロン辺を除去すると、もともとはGとHの入り口だったノードは不達ノードになるのでこれも除去します。こうして最終的に出来上がったグラフは“扱いやすいオートマトン”です。
明瞭正規表現の構成に関する「First(E)∩First(F) が空集合」という条件は、この操作により非決定性が生じないために必要だったのです。
G+ の構成
Gの終状態と出口を結ぶ辺をイプシロン辺に変えて、Gの出口(プラス)と入り口(マイナス)を重ねます。記号はマイナスのままにしておきます。
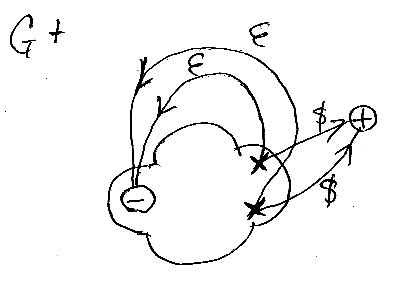
この操作によりイプシロン辺が何本かできるので、すべてのイプシロン辺を除去します。
イプシロン辺を除去すると、Gの入り口だったノードは不達ノードになりますが、入り口として使い続けるので除去しません。こうして最終的に出来上がったグラフは“扱いやすいオートマトン”です。
明瞭正規表現の構成に関する「FollowLast(E)∩First(E) が空集合」という条件は、この操作により非決定性が生じないために必要だったのです。
Q.E.D.
これで帰納法による証明は終りです。それと同時に、与えられた明瞭正規表現をオートマトンにコンパイルする具体的な構成法も示したことになります。
正規表現を構成する基本的な演算子として '?', ',', '|', '+' を取りましたが、別の選択をしてもかまいません。“扱いやすいオートマトン”の条件はかなり強いものでしたが、もう少しゆるめたり変更しても同様な構成と証明が通用します。状況に応じてカスタマイズしてください。
明瞭正規表現の問題点
明瞭正規表現の動機は、正規表現のなかで「コンパイルが簡単で実行が高速」になるようなサブセットを定義することでした。もともとがご都合主義的な概念なので、欠点/問題点もあります。
言語Lが明瞭正規言語であることを、明瞭正規表現Eが存在して L = 《E》 と書けることだとします。こうして定義される明瞭正規言語全体の言語クラスはあまりいい性質を持ちません。連接、合併、繰り返しが自由に出来るわけではなくて制約があることが色々とネックになります。
しかし、簡単かつ高速であることの優先度が高いときは明瞭正規表現を考慮する価値があります。また、明瞭正規表現の実装を中心に置いて、他の方法を併用したり、部分的に拡張するというやり方もあります。
Catyの型システムは正規表現型の貧弱なサブセットしか持ってませんが、それでもかなりの事が出来ている*7ことから見て、完全な正規表現型ではなくて明瞭正規表現型でも、多くの応用では十分な気がします。
*1:グラフGも明示して、indeg(G, x) のように書いたほうが正確ですが、文脈からGが分かるときは省略します。
*2:不達ノードの存在を認めないのでzが存在できないときがあるのです。「出口は不達でもいい」とすれば、必ずzが存在するようにもできます。
*3:明瞭オートマトンと呼んでもいいのですが、正規表現の明瞭性に対応する性質以外に、扱いやすさのための便宜上の条件も仮定しているので、そのまんま「扱いやすい」にしました。
*4:この選択にも冗長性があります。定数と演算子の集合を極小にすることは目的にしてません。
*5:今回使う変形以外にも重要な変形方法はあります。
*6:プラスとマイナスを使う理由は「この機会にマスターしようぜ、正規表現、構文図、オートマトン」を見てください。
*7:Catyは、シーケンス型とは別にバッグ型(マルチセット型)を持っています。正規表現型よりバッグ型のほうが実用上は多用するかもしれません。