ストリング図の基本概念と描き方

僕がやっているセミナーのなかでストリング図を描く練習をしたのですが、ストリング図の基本的（ほんとに基本的）なことを復習したほうがいいかな、と感じました。ほんとに基本的なことは意外と言及されてないので。

内容：

ストリンググラフ

ストリング図は、グラフ理論で扱うグラフのようなものですが、標準的なグラフの定義ではストリング図を記述できません。ストリング図は開放辺〈{open | half | dangling} edge〉を持ちます。開放辺とは、辺の片側がノードになっていない辺です。

ストリング図をグラフ理論で扱えるようにするためにストリンググラフという概念を使います。これについては次の記事で書いたことがあります。（が、以下、過去記事を参照しなくてもよいように書きます。）

• ストリング図とストリンググラフ、何が違う？
• ストリンググラフとストリング図

ストリンググラフ〈string graph〉に関して簡単に復習しておくと：

1. ストリンググラフの台構造〈underlying structure〉はグラフ理論の意味での有向グラフ である。
2. 頂点の集合 は と分解される。
3. 幾つかの条件を満たす。

幾つかの条件については、今は気にしなくていいです。出てきた記号を説明すると：

• ： 有向グラフの辺〈edge〉の集合
• ： 有向グラフの頂点〈vertex〉の集合
• ： 辺に始点〈source〉を対応させる写像
• ： 辺に終点〈target〉を対応させる写像
• ： ワイヤー頂点〈wire vertex〉の集合。以下、単に と書く。
• ： ノード頂点〈node vertex〉の集合。以下、単に と書く。

通常、「頂点」と「ノード」は同義語ですが、ここでは、ノードは頂点の特別なもので、ノード〈ノード頂点〉以外にワイヤー頂点があります。ワイヤー頂点の導入が、ストリンググラフのキモと言えます。次節でワイヤー頂点の意義と用途を説明します。

ワイヤー頂点

ストリング図を描くソフトウェアを作る立場になると、ワイヤー頂点の必要性は身に沁みて分かります。実際、ストリンググラフの理論は、ソフトウェアQuantomatic（https​://quantomatic.github.io/）の背景理論となっています。なので、描画ソフトウェア作成を想定して読むといいでしょう。

次は簡単なストリング図の例で、モノイド圏の射 を表しています。

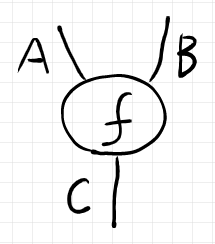
ここで、ノードを大きさを持つ丸で描いているのは、ラベルを記入するためで、大きさを持たないドットで描いてもかまいません。ラベルを取り去った形状だけ描くと次のようになります。

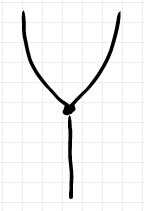
辺が3本に対して頂点が1個なので、グラフ理論の意味の有向グラフにはなりません。辺に始点／終点を対応させる をうまく定義できません。そこで、次の図の青い頂点を追加します。もともとあった頂点は赤で描きました。

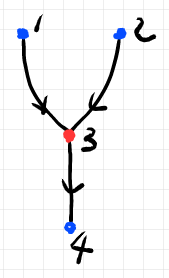
青い頂点は“開いた端点”〈open endpoint〉を表すものです。もともとあった赤い頂点には圏の射を割り当てます。（辺には圏の対象を割り当てます。）

すべての頂点に番号を振って辺に向きを付ければ、通常の有向グラフになります。単純グラフ（多重辺や自己ループ辺を持たないグラフ）なので、辺に名前・番号は不要です。この有向グラフを具体的に書き下すと次のようになります。

• 頂点の集合：
• 辺の集合：
• 始点：
  
• 終点：
  

これに次の情報を付け加えるとストリンググラフになります。

• ワイヤー頂点の集合：
• ノード頂点の集合：

ストリンググラフのノード頂点がストリング図のノードになり、ワイヤー頂点は開いた端点（あるいは境界点）になります。例えば、デカルト座標が入った通常の平面にストリング図を描くとき、ノードの位置座標だけでなくてワイヤーの開いた端点の位置座標も必要なのは明らかでしょう。

ワイヤー頂点は開いた端点〈境界点〉以外の用途でも使われます。それはワイヤー内の中間の点としてです。これに関しては次の図（https​://arxiv.org/pdf/1504.02716.pdf から引用、描画方向は下から上）を見るとすぐ分かるでしょう。

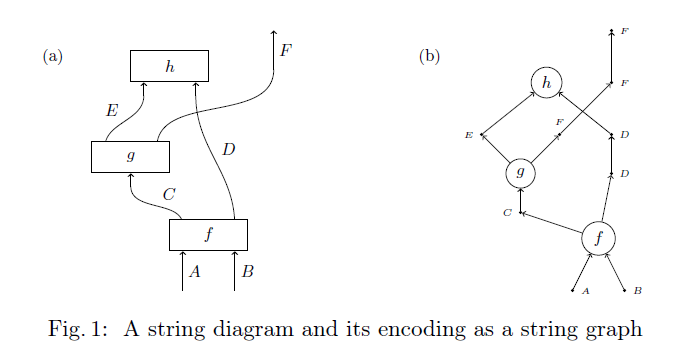
描画ライブラリが直線しか描けないとして、曲線（左側の図）を折れ線（右側の図）で代用する状況を考えます。そのとき、折れ線の“折れる点”がワイヤー頂点になります（実は折れてなくてもいいんだけど）。曲線が描けるとしても、何かの目印の点とか制御点とかで、ワイヤーの中間の点が必要になることがあります。また、曲線を折れ線で近似することは理論上も重要です。

以上に説明したように、ワイヤー頂点の用途は次の2つです。

1. ワイヤーの開いた端点〈境界点〉を表す。
2. ワイヤー内の中間の点を表す。

それぞれ次のように呼びます。

1. 境界ワイヤー頂点〈boundary wire vertex〉
2. 内部ワイヤー頂点〈interior wire vertex〉

境界ワイヤー頂点は単に境界頂点とも呼び、進入境界頂点（incoming boundary vertex）と退出境界頂点（outgoing boundary vertex）に分類できます。

キャンバスと描画方向と禁則

ストリング図は平面に描くとして、その平面をキャンバス〈canvas〉と呼びます。3次元以上の空間に描くことは今は考えません。

キャンバスには常識的なデカルト座標を入れて とみなします。キャンバスは単なる点の集合ではななくて、距離や角度も考えられるユークリッド・アフィン空間*1です。「x軸、y軸」は常識的な意味で使います。

ストリング図は一種の有向グラフですが、ワイヤーに矢印を描くことはほとんどありません。その理由は、前もって描画方向を約束しているからです。射の結合の方向を第一方向、モノイド積の方向を第二方向とすると、描画方向の約束は8種類あります。

番号	第一方向	第二方向	略記
1	x軸正方向	y軸正方向	→↑
2	x軸正方向	y軸負方向	→↓
3	x軸負方向	y軸正方向	←↑
4	x軸負方向	y軸負方向	←↓
5	y軸正方向	x軸正方向	↑→
6	y軸正方向	x軸負方向	↑←
7	y軸負方向	x軸正方向	↓→
8	y軸負方向	x軸負方向	↓←

すべての描画方向が使われているという話は次の記事でしました。

• 絵算（ストリング図）における池袋駅問題の真相

僕が個人的に使っている描画方向を示すマーカーは“旗”です。それについては：

• 絵算の描画方向を示すために旗を使うことにした

ストリング図は好き勝手に描いていいものではありません。あまり言及されませんが（僕も明示的に書いた／言ったことがなかった）禁則があります。

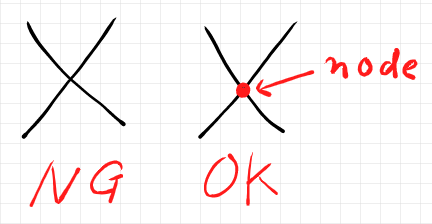
• 禁則1： ワイヤーを交差させてはいけない。

「交差させているのをよく見るぞ」と思う人もいるでしょうが、あれは違うんですよ。ワイヤーを交差させているのではなくて、交差点にノードがあるのです。見た目では、「ワイヤーの交差」と「交差点にノード」が区別できないときがありますが。

[追記]読み返したら、上に挙げた A string diagram and its encoding as string graph の図にワイヤーの交差がありますね。2次元キャンバスに埋め込んではいない抽象的・組み合わせ的な状況かも知れません。2次元キャンバスに描く場合は、対称モノイド圏の対称とワイヤーの交差の区別が出来ないので、ワイヤーの交差はやっぱりNGです。[/追記]

次に、描画方向とワイヤーの方向の関係です。これは、ほんとに暗黙に前提されていることで、明示的に書くのが難しいのですが ‥‥ 以下に記述します。

第一／第二の描画方向を示すために、その方向の単位ベクトルを取ります。例えば、描画方向「↓→」の第一描画方向のベクトルは です。

ワイヤーが折れ線の場合は折れ線のセグメント（折れ線を構成する有向線分）、ワイヤーが曲線のときは接ベクトルを考えます。これらのベクトルを長さ1に正規化してワイヤーの（特定の点での）方向ベクトルとします。

さて、描画方向の方向ベクトルとワイヤーの方向ベクトルを使って禁則を記述できます。

• 禁則2： 第一描画方向の方向ベクトルとワイヤーの方向ベクトルのなす角が90度以上になってはいけない。

通常のユークリッド内積を使って言えば：

• 禁則2： 第一描画方向の方向ベクトルとワイヤーの方向ベクトルの内積は0以下になってはいけない。

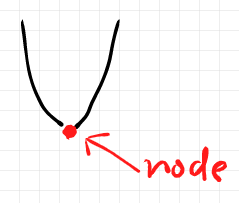
これに関しても「描画方向と逆向きに走るワイヤーを見たぞ」とか「曲がったワイヤーが描けないだろ」とか思うでしょうが、違うんですよ。「逆向きに走るワイヤー」じゃなくて、負の極性〈polarity〉を割り当てられたワイヤーをあたかも逆向きに走るワイヤーのように描く習慣があるだけです*2（便利ですけどね）。曲がったワイヤーの正体は次のようなものです。[追記]詳しくは「ストリング図の基本概念と描き方： 補遺」参照。[/追記]

以上の禁則は、モノイド圏の記述・計算に使われるストリング図に関する禁則です。別な状況では話が変わります。

例えば、3次元空間に描かれたストリング図を2次元に射影すると、ノードには対応しないワイヤーの交差が（影として）現れます。

テンパリー／リーブ圏の射（「テンパリー／リーブ圏とカウフマンのスケイン関係式」参照）の図（カウフマン図）に出てくる曲がったワイヤーは「ほんとに曲がっている」と解釈してもいいでしょう。モノイド圏で解釈する前は、単なるアイコン〈ピクトグラム〉なので、アイコンの絵柄にまで禁則を適用する必要はありません。

圏論的オペレーター〈圏論的コンビネータ〉が作用した目印に曲がったワイヤーを使うことがあります。例えば、マルコフ圏に働く条件化オペレーターの作用を曲がったワイヤーで描きます。この場合は曲がったワイヤーはノードに対応しません*3。

スパイダーノード

前節の曲がったワイヤーのように、ほんとはノードがあるのだけど明示的に描かないケースはけっこうあります。この“明示的に描かないノード”は、ワイヤー頂点とはまったく別です。ワイヤー頂点はノード〈ノード頂点〉じゃないです。“明示的に描かないノード”はノードです。つまり、圏の射が割り当てられます。ぜんっぜん違う。

いま、デカルト圏におけるストリング図を描くとしましょう。デカルト圏には次のような特別な射があります*4。

1. ： 恒等射
2. ： 終対象への唯一の射
3. ： 対称射〈スワップ | 入れ替え | 互換〉
4. ： 対角射

これらの射は、ノードらしく描かないで、それぞれ次のように描きます。

1. ： ワイヤーだけ
2. ： 途切れたワイヤー
3. ： ワイヤーの交差
4. ： ワイヤーの分岐

ノードらしく描かないのでノードじゃないと誤解されがちですが、ノードです！

ノードらしく描かないノードに対応する射は、圏の構造を決めている場合が多く、基本スパイダー射〈{elementary | basic | atomic | primitive} spider morphism〉と呼びます。もちろん、この定義は曖昧で何言ってるかわからないのですが、モノイド圏 に射の集合 を指定した構造 における の要素が基本スパイダー射です。基本スパイダー射を任意に決めることが出来ますが、多くの場合は圏の構造を決めている射です。基本スパイダー射を割り当てられたノードがスパイダーノード〈spider node〉です。

基本スパイダー射から生成される最小の部分モノイド圏の射は（一般の）スパイダー射〈spider morphism〉です。スパイダー射を表すストリング図は、ワイヤーが繋がっているだけでノードがないように見えます。そう見えるだけでノードはあります。

「スパイダー」という言葉は一部の人（例えば「ダンジョン圏における確率伝搬法」で紹介したモートン）しか使ってませんが、便利な言葉なので僕はよく使います。

*1:ユークリッド・アフィン空間とは、平行移動として作用するベクトル空間が内積を持つベクトル空間であるようなアフィン空間です。

*2:例えば、とあるベクトル空間を順方向のワイヤーで表して、その双対空間を逆方向のワイヤーとして描画するとかです。もとのベクトル空間と双対空間は逆な極性を持つと考えます。

*3:オペレーターをノード（圏の射）で書けることもありますが。

*4:象形文字記法を使うなら、 。