因果セオリー論〈theory of causal theories〉という奇妙な言葉については直前の記事「フォングの“因果セオリー”の理論」を見てください。
直前の記事において、フォングのストリング図は「視認性が悪く、おすすめできませんね。」と否定的な言い方をしたのですが、あの図法で描くにはそれなりの理由があり、フォングのアイディアが潜んでいます。そのアイディアとメリットを説明せずに「視認性が悪い」で片付けるのはいかがなものか? と反省したので追加説明をします。
とはいえ、語法・記法・図法で、やっぱり直したほうがいいだろうと思う点はあるので、それは指摘します。
内容:
普通の言葉にしよう
まず最初に、フォングの独特の用語を、比較的に一般的(だと思われる)用語で代替しましょう。
| フォングの用語 | 代替の用語 |
|---|---|
| 因果セオリー | 厳密マルコフ圏 |
| 因果モデル | グラフィカルモデル |
| 因果構造 | グラフィカルスキーマ |
| 確率変数 | 頂点 |
| 因果関係 | 辺 |
| 因果機序*1 | 固有生成射 |
| コモノイド射 | コモノイド射(同じ) |
フォングの因果セオリー論、スピヴァックの関手データベース論、ローヴェアの代数セオリー論は、同じ手法を異なる分野に適用している例です。分野ごとに異なった固有の語法・記法・図法を採用したほうがいいこともあるでしょうが、共通化してもいいところは出来るだけ共通化する方針にします。
ローヴェアの用語「セオリー」を尊重したい気持ちは分かるんですが(ローヴェアは偉大なパイオニアですからね)、「セオリー」はやめよーよ。因果セオリーは、マルコフ圏にモノイド圏としての厳密性〈strictness〉を追加した構造なので、そのまんま厳密マルコフ圏〈strict Markov category〉とします。
因果モデルの代替語は、けっこう普通に使われているグラフィカルモデル〈graphical model〉。ベイズ・ネットワーク〈Bayesian Networks〉はグラフィカルモデルの同義語です(ニュアンスは知らん)。因果モデルは、通常のグラフィカルモデルよりずっと一般的だと言えますが、それを強調したいなら一般化グラフィカルモデル〈generalized graphical model〉とか形容詞付ければいいでしょう。
グラフィカルモデルの、有向グラフ(単なる図形)だけを抜き出しのがグラフィカルスキーマ〈graphical schema〉です。「スキーマ」はデータベース用語ですが、スピヴァックはデータベース用語をそのまま流用してます(分野がデータベースなので)。データベースのスキーマは、実際のデータを与える前の構造指定ですが、グラフィカルモデルのスキーマも確率的情報を与える前の構造指定(の絵)です。
因果構造〈グラフィカルスキーマ〉は、因果セオリー〈厳密マルコフ圏〉の生成系〈generator | generating system〉となりますが、もとの有向グラフの辺から作られる射が因果機序(固有生成射〈proper generating morphism〉で代替)で、コモノイド構造を与えるための射がコモノイド射〈comonoid morphism〉(対角射と終射)です。
グラフィカルスキーマ
さてここからは、フォングがなぜ次のような独特なストリング図を描いたかを説明しましょう。
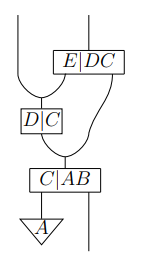
上のストリング図のもとになっているのは、次のようなグラフィカルスキーマ〈因果構造〉です。ストリング図とグラフィカルスキーマは、まったく同じことを異なる図法で表現しています。
グラフィカルスキーマでは、矢印〈有向辺〉の根本を親〈parent〉、先頭を子〈child〉と呼びます。そう呼ぶのは習慣、必然性を持たない根拠なき選択です。
ひとつの頂点に、複数の親があるときは、それを並べますが、並べる順序を決めておきます。上の図で (1), (2) という番号は親の順番です。
- Cの親は A, B (B, Aではない)である。
- Eの親は D, C (C, Dではない)である。
複数の子にも順番が必要ですが、図には書き込んでありません。
- Cの子は、D, E (E, Dではない)である。
- Dの子は、D(コピー), E (E, Dではない)である。
頂点に入る/頂点から出る辺に順番が付いているグラフをファットグラフ〈fat graph〉(またはリボングラフ〈ribbon graph〉)と呼びます*2。グラフィカルスキーマはファットグラフである必要があります。
フォングの定義では、グラフィカルスキーマ〈因果構造〉がファットグラフであることを要求していません。グラフィカルモデル〈ベイズ・ネットワーク〉のグラフでは、辺の順番(ファット構造)を考えることがないからでしょう。しかし、辺の順番を与えるのはたいした手間じゃないし、後々の扱いが分かりやすくなります。
文字通りグラフィカル〈視覚的〉に与えられたグラフィカルスキーマを、テキストで書き下します。とりあえず、頂点を集合、辺を関数〈写像〉だと思って、関数の名前とプロファイル(域と余域)を並べていきます。関数の名前とプロファイルを並べたものを指標〈signature〉と呼ぶので、グラフィカルスキーマを指標として書き下すことになります。
signature Sample {
operation e:I→A
operation f:A,B→C
operation g:C→D
operation h:D,C→E
operation i:D→D
}幾つかの注意事項:
- 図の小さい黒丸の頂点は I とする。Iからの関数は図では点線矢印。
- 関数(operation と書いてある)に、図にはない名前を付ける。ここでは e, f, g, h, i 。
- 複数の親からひとつの子に向かう矢印達は、まとめてひとつの関数〈operation〉とする。f:A,B→C と h:D,C→E はその例
- 図の太い矢印は恒等関数を表す。i:D→D は idD:D→D のこと。
グラフィカルスキーマのままでは圏論的解釈がしにくいので、ストリング図に描き変えていきます。絵図を変形するスキル(習えば小学生でも出来ること*3)が必要になります(「双対や随伴に強くなるためのトレーニング」参照)。
ストリング図への描き換え
圏論的確率論の多数派は「下から上」なので、まず図の上下をひっくり返します。
次にポアンカレ双対*4をとります; これは、辺を頂点〈ノード〉に、頂点を辺〈ワイヤー〉に置き換えることです。実際にその作業をしているときのスキャン画像は次のようです。
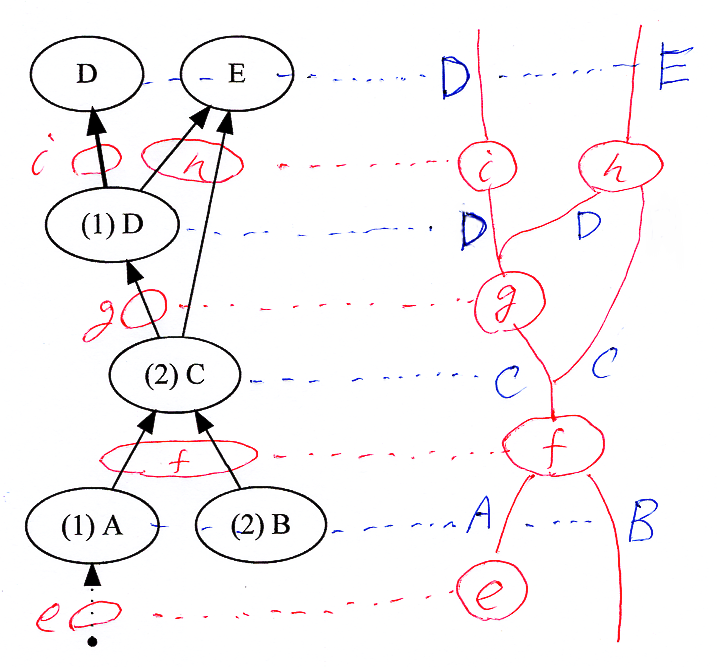
グラフィカルスキーマでは分かりにくかった枝分かれがハッキリしました。i は恒等 idD を意味するので描く必要はありません。ノードのアイコンを三角や四角にするのは好みの問題/約束の問題です。
でき上がったストリング図は、トポロジカルに(繋がり具合として)は、フォングのストリング図と同じことは分かるでしょう。しかし、フォングは“謎のラベリング”をしています。これは何なのでしょう?
フォングのラベリング
もう一度、グラフィカルスキーマに対応する指標を見てみます。
signature Sample {
operation e:I→A
operation f:A,B→C
operation g:C→D
operation h:D,C→E
operation i:D→D
}このなかで、i は idD と書けばいいし、ストリング図ではどうせ省略するので、まーどうでもいいです。残りのオペレーション(関数みたいなもの、実は圏の射)には名前を与えています。しかし、有向グラフが単純な場合、両端を決めればオペレーションが決まってしまうので、あえて名前を付ける必要はありません。
オペレーションの名前の代わりに、両端を [子|親の並び] の形で書きます。この記法を使って指標を書き換えると:
signature Sample {
operation [A|I]:I→A
operation [C|A,B]:A,B→C
operation [D|C]:C→D
operation [E|D,C]:D,C→E
operation [D|D]:D→D
}ノードへのラベルをこの書き方にします。フォングはさらに、親の並びのカンマも省略しています、[C|A,B] = [C|AB] のように。また、[A|I] = [A|] = [A] という略記も使います。ノードに入るワイヤー/出るワイヤーの情報もラベルに含まれるので、ワイヤーへのラベルが不要になります。フォングのストリング図を再掲:

条件付き確率の記法に合わせたのだ
これでもまだ、フォングのラベリングの動機が分かりません。実は、フォングのラベリングは、同時確率分布、周辺確率分布、条件付き確率などの記法に合わせているのです。
伝統的な確率論では、同時確率、周辺確率、条件付き確率などにすべて同じ文字(例えば'P')を割り当てます。初学者にはとても分かりにくく難儀しますが、便利なのも確かです。例えば、P(B) = P(B|A)P(A) とか。フォングのラベリングは、この等式を、関手Pに関する等式 P([B]) = P([B|A])P([A]) と解釈する道具なのです。
グラフィカルスキーマから作られた厳密マルコフ圏〈因果セオリー〉の射は、スキーマに現れた(id以外の)射 [A|I] = [A|] = [A], [C|A,B], [D|C], [E|D,C] と、ΔX(Xの対角射、枝分かれ)と !X(Xの終射、破棄)を組み合わせて作れます。それらの射に、確率的な概念(同時確率分布、周辺確率分布、条件付き確率など)を対応させる関手がグラフィカルモデル〈因果モデル〉で、それを'P'などの1文字で表すわけです。
これは見事なトリックだと思います。が、僕は習慣的記法に合わせる意義を感じません。言い換えれば、習慣的記法に価値があるとは思えないのです。なので、フォングのラベリングは見にくいだけ、と思ってしまいます(ゴメンね)。
私見はさておき、フォングの独特なストリング図には、ちゃんとした理由と巧みなアイディアがあったのだ、ということです。
オマケ: Graphvizのdotソースコード
この記事内のグラフは、「データをURLに保存する: GraphvizOnlineの方法」で紹介したGraphvizOnlineで描いています。
- https://bit.ly/2YRIYsa (上から下)
digraph G { I [shape=point] A [label="(1) A"] B [label="(2) B"] C [label="(2) C"] D [label="(1) D"] D2 [label="D"] E I -> A [style=dotted] A -> C B -> C C -> D D -> E C -> E D -> D2 [style=bold] }
- https://bit.ly/2YNSLzI (下から上)
digraph G { graph[rankdir=BT] I [shape=point] A [label="(1) A"] B [label="(2) B"] C [label="(2) C"] D [label="(1) D"] D2 [label="D"] E I -> A [style=dotted] A -> C B -> C C -> D D -> E C -> E D -> D2 [style=bold] }
ポアンカレ双対をとった後はこんな(↓)かな。
digraph G { graph[rankdir=BT] I_A [label="[A|]"] AB_C [label="[C|AB]"] C_D [label="[D|C]"] DC_E [label="[E|DC]"] B[shape=none, label=""] D[shape=none, label=""] E[shape=none, label=""] I_A -> AB_C [label="A"] B -> AB_C [label="B"] AB_C -> C_D [label="C"] C_D -> DC_E [label="D"] AB_C -> DC_E [label="C"] DC_E -> E [label=E] C_D -> D[label=D] }