カン拡張のために、柱の絵を描く

この記事は、ゆっくりと具体的にカン拡張へと近づいて行こう、という試みの一環です。カン拡張の説明に、ペースティング図やストリング図は必須ですが、もっと“写実的”な描画法として、点と矢印が錯綜する空間内に描出される“柱”の絵を描いてみます。

内容：

極限からカン拡張へ

特にシリーズ記事とかにしませんが、関連する幾つかの記事達が、全体としてカン拡張の説明になればいいな、というゆるい計画はあります。それら関連する記事とは：

• 圏論の随伴をちゃんと抑えよう
• 圏論の随伴をちゃんと抑えよう： お絵描き完全解説
• カン拡張における上下左右： 入門の前に整理すべきこと
• 圏論の極限を具体的に

カン拡張は非常に一般的な概念なので、その解釈／説明の仕方は色々とあるでしょう。どういう切り口がいいのかは一概には判断できませんが、僕は「カン拡張は極限の一般化である」という解釈が分かりやすいような気がしています。

極限の標準的な定義は、「圏論の極限を具体的に // 関手の極限の復習」で述べたように「錐の圏の終対象」です。極限概念を一般化するなら、「“錐を一般化したナニカ”の圏の終対象」として右カン拡張（「“余錐を一般化したナニカ”の圏の始対象」として左カン拡張）を定義するのが素直なやり方でしょう。

しかし、“錐を一般化したナニカ”を前面に出した方法って、あまり見かけません（探せばあるとは思いますが）。ここでは、“錐を一般化したナニカ”を柱〈ちゅう | はしら | cylinder〉と名付けて、柱の定義と描画法を述べることにします。柱の圏に慣れれば、カン拡張にも近づきやすくなるでしょう。

再び上下左右に関する注意

圏論では、「左」「右」という形容詞をよく使います。「上」「下」に関する形容詞（upper/lower, over/under, top/bottomなど）も使われます。しかし、ほとんどの場合、現実世界の上下左右とは何の関係もありません。2つのモノ、あるいは4つのモノを区別する符丁（隠語、目印）として上下左右が使われているだけです。

以下では、記憶を助けるため／印象を鮮明にするために、現実世界の上下左右を比喩的に持ち出しますが、これらはすべて方便です。したがって、左ナントカを右側に書くときもあるし、上に、あるいは下に書くかもしれません。圏論では、双対により上下左右がコロコロ入れ替わるので、「左」と名付けたモノは必ず左に書く（描く）というのは困難なのです。（それゆえに、トレーニングが必要。）

ツリーの図を描くときに、ルート（根）が上でリーフ（葉）が下に描くほうが多数派だと思います。ルートが上でも左でも右でも、ツリーの絵であることに変わりはありません。「ツリー」という名称は、イマジネーションを喚起する良い名前だと思いますが、ツリーの絵が、実在の植物の写生である必要はありません。

こんな言ワズモガナな注意をするのは、専門用語の語源・語感に拘って、不毛な詮索やつまらない誤解に陥る人をけっこう見受けるからです。また、絵図の描画方法や描画方向を変えてしまうと、同じ絵だと認識するのがけっこう難しいのです*1。

錐と柱

錐に関しては次の言葉を使いました（「圏論の極限を具体的に // 関手の極限の復習」参照）。

• 錐〈cone〉
• 頂点〈apex | vertex | peak〉
• 底面〈base〉

錐に対して柱とは、およそ次のような図形です。

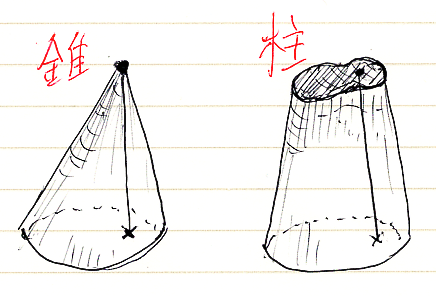
「底面」は柱に対してもそのまま使い続けたいと思います。「頂点」という言葉はとんがった一点のイメージが強いので、柱に対して「頂点」を使うのは無理があります。“底面でないほうの面”を何と呼ぼうか？ しばらく考え込んでしまいました。

こんなとき、安直に「上下左右」が使われるのです。「上面と下面」「左面と右面」とか。もうひとつの安直なネーミングルールに、片一方に「余」を付ける方法があります -- こっちを採用します。柱の“底面でないほうの面”を余底面〈cobase〉と呼ぶことにします。

錐の頂点から出て底面に至る線は成分線〈component {segment | arrow | line}〉と呼ぶことにしました（これも「圏論の極限を具体的に // 関手の極限の復習」参照）。柱でも同じ言葉を使います。先の図に、錐の成分線と柱の成分線が一本ずつ描いてあります。

3次元立体としての錐と柱は、成分線が束になって作り出されていると考えましょう。成分線の束としての立体を特に錐体〈cone body〉、柱体〈cylinder body〉と呼ぶことにします。

錐	柱
頂点	余底面
底面	底面
成分線	成分線
錐体	柱体

これらの図形的な言葉の圏論的な意味は次節以降で説明します。

錐の再分析

錐については、「圏論の極限を具体的に // 関手の極限の復習」で述べてますが、もう少し精密に分析してみます。

実は、「錐」「頂点」「底面」などの言葉は多義的に使われています。そのことを、次の図を見ながら考えていきましょう。

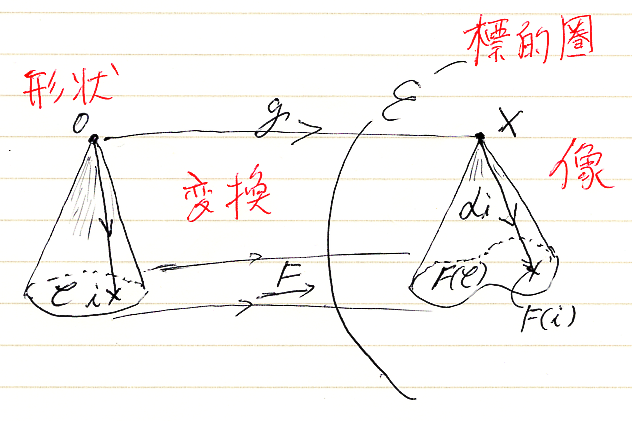
しばしば「底面F」という言い方をしてきましたが、Fは圏Cから圏Eへの関手です。関手Fに関連して、次のような概念が一緒に登場します。

• 関手の域である圏C
• 関手Fそのもの
• 関手の像であるEの部分圏F(C)

「底面」は、これらのどれでも表す言葉で、文脈によりどれかを表しています。同様に、「頂点」や、成分線の束としての「錐体」なども多義的に使われることになります。

このまま多義的な言葉の使用（オーバーローディング）を無節操にしていると、混乱に陥るので、面倒でも（一旦は）区別することにします。

まず関手Fの余域である圏Eを、錐の標的圏〈target category〉と呼びます。一方、圏Cは錐の底面形状〈base shape〉を与えます。錐の形状〈shape〉は、標的圏Eの外部にある図形です。形状は、単元集合である（形状の）頂点を持ち、単なる形式的な矢印である成分線を持ちます。Eの外部にある錐の形状が、変換〈transformation〉により、E内の像として描出〈rendering〉されます。

錐の構成要素を細かく分ければ次のようになります。Obj(-)は対象の全体、Mor(-)は射の全体です。

	形状	変換	像
頂点	{0}	g:{0}→Obj(E)	g(0) = X
底面	C	F:C→E	F(C)
錐体	{0}×Obj(C)	α:{0}×Obj(C)→Mor(E)	{αi∈Mor(E)| i∈Obj(C)}

錐体は成分線の束でした。形状側の一本の成分線は、i∈|C|に対する(0, i)の形をしています。(0, i)←→ i と1：1対応するので、Cの対象と同一視可能ですが、図形的には成分線と底面の一点は別物です。αは、形状側成分線の束をEの射の束に変換します。像側の成分線は、α_i:X→F(i) というEの射です。一本の成分線に関する変換は、(0, i) |→ α(0, i) = α_i として与えられます。

結局、正確な話をしたいなら、次のような用語をすべて区別することになります。

1. 頂点形状 {0}
2. 頂点変換 g:{0}→|E|
3. 頂点像 g(0) = X ∈|E|
4. 底面形状 C
5. 底面変換 F:C→E
6. 底面像 F(C) ⊆ E
7. 錐体形状 {0}×|C|
8. 錐体変換 α:{0}×|C|→Mor(E)
9. 錐体像 α({0}×|C|) ⊆ Mor(E)
10. 成分線形状 (0, i) ∈ {0}×|C|
11. 成分線変換 (0, i) |→ α(0, i) = α_i
12. 成分線像 α_i:X→F(i) in E

さすがに面倒くさいので、適当にオーバーロード（多義語の使用）をすることになります。

自然変換としての錐

錐は、ひとつの自然変換として表現できます。このとき、単一対象と恒等射だけの圏（一点離散圏）を使います。ここでは、一点離散圏〈終圏 | 自明圏 | 単位圏〉を☆で表します。

• |☆| = {0}
• Mor(☆) = {id₀}

☆は“圏の圏”の終対象なので、圏Cから☆への関手がただひとつあります。それを、!_CまたはBang_Cと書きます。

X∈|E| を選ぶと、X~:☆→E という関手（対象Xをポイントする関手）が次のように定義できます。

• X~(0) = X
• X~(id₀) = id_X

また、X∈|E| を選ぶと、Xに値を取る定数値関手 Const_X:C→E が次のように定義できます。

• すべての i∈|C| に対して、Const_X(i) = X
• すべての φ:i→j in C に対して、Const_X(f) = id_X

次の等式が成立します。

• Bang_C*X~ = Const_X

ここで、'*'は関手の図式順結合の記号です。反図式順なら、

• X~・Bang_C = Const_X

さて、錐体変換 α:{0}×|C|→Mor(E) は、α:|C|→Mor(E) と考えても同じです。そして、次の錐条件〈cone condition〉を満たします。

• すべての φ:i→j in C に対して、α_i;F(φ) = α_j in E

この条件は、可換図式として次のように書き換えられます。

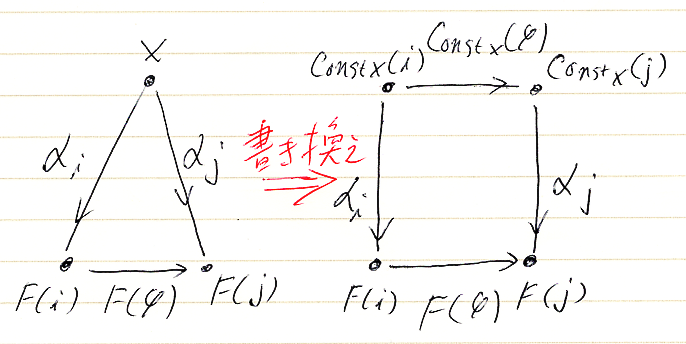
つまり、αは、関手Const_Xから関手Fへの自然変換です。

• α::Const_X⇒F:C→E

Bang_C*X~ = Const_X を使えば：

• α::Bang_C*X~⇒F:C→E

この形を使って、錐から柱への一般化を行います。Bang_Cを一般的な関手 K:C→D に、X~を一般的な関手 G:D→E にして、

• α::K*G⇒F:C→E

とすれば、Gとαが柱を表します（次節以降で詳述）。

柱の絵と定義

まずは柱の絵を出します。

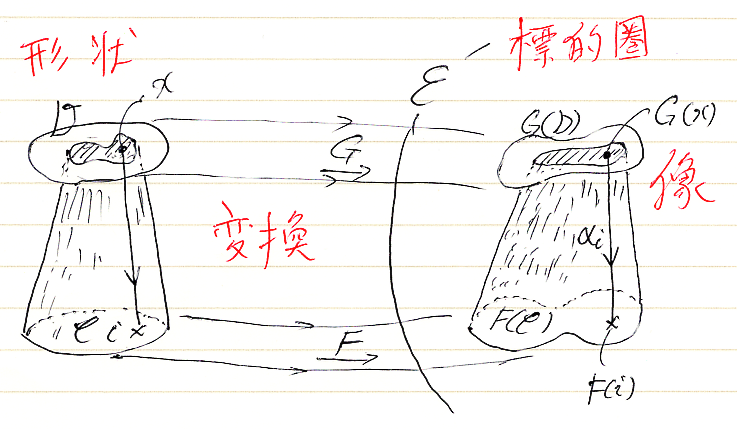
と、こんな感じです。錐の場合と同様に、標的圏Eがあり、形状から標的圏への変換により柱が描出され、圏E内に像が現れます。

底面 F:C→E は錐の場合と変わりません。余底面形状は、単なる圏Dではなくて、Dの部分圏D'（斜線で塗ってある所）があり、（形状側の）成分線は、D'から底面形状Cへと向かいます。余底面の変換は、関手 G:D→E で与えられます。形状側の成分線(x, i)に対する像側の成分線は、α_i:G(x)→F(i) というEの射です。柱体変換は、|D'|×|C|の部分集合（後述）からMor(E)への写像αとなります。

ここで、柱の形状側を詳しく見ましょう。

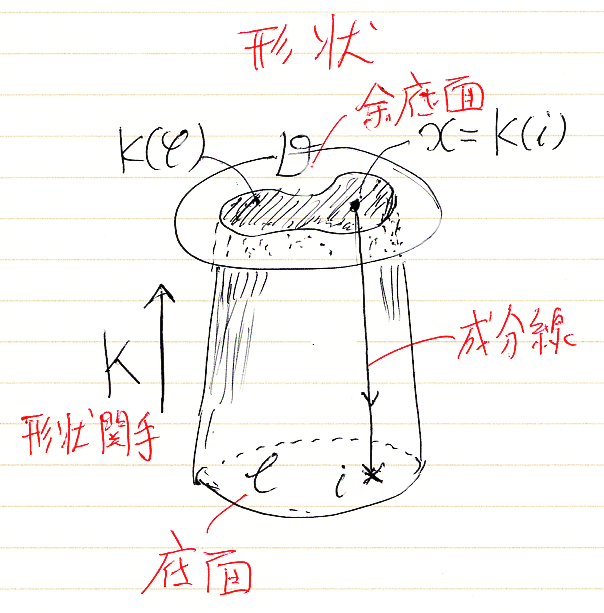
柱の形状は、底面から余底面への関手 K:C→D で与えられます。Dの部分圏D'とは、関手Kの像K(C)なのでした。図で、関手Kは下から上に向かってますが、成分線の向きは上から下です。一本の成分線は、i∈|C| に対して、K(i)からiに向かいます。Kが柱が形状を決定しているので、Kを（柱の）形状関手〈shaping functor〉と呼ぶことにします*2。

形状余底面を☆にして、形状関手を Bang_C:C→☆ とすると、錐の形状になります。つまり、錐は、形状関手がBang_Cであるような柱として再定義されます。

錐に錐条件があったのと同様に、柱には柱条件〈cylinder condition〉があります。それは、像側に出来る断面四角形が、E内で可換図式になることです。

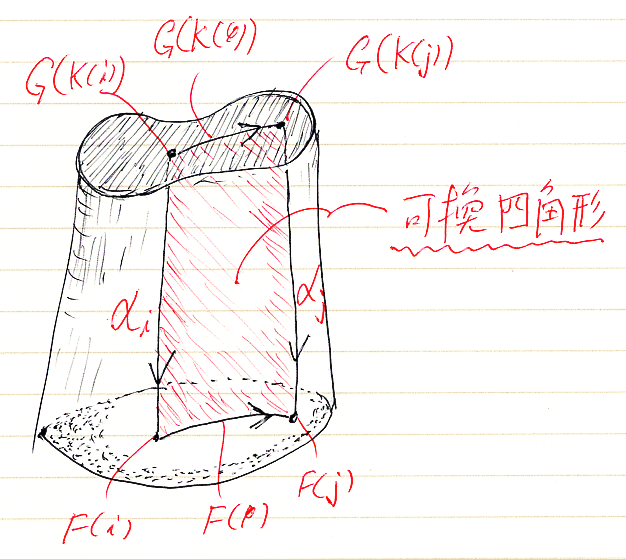
• すべての φ:i→j in C に対して、α_i;F(φ) = G(K(φ));α_j in E

柱条件の四角形を三角形に退化させると錐条件になるのは分かるでしょう。

自然変換としての柱

錐を関手 α::Bang_C*X~⇒F:C→E と解釈したのと同じ方法で、柱も自然変換と解釈できます。

αの形を見ると、形状関手Kと余底面の変換Gを結合した関手K*Gから、底面の変換Fへの自然変換になっています。柱条件がαの自然性〈naturality〉になっています。

• i∈C ごとに、α_i:G(x)→F(i)
• x = K(i) なので、α_i:G(K(i))→F(i)
• すべての φ:i→j in C に対して、α_i;F(φ) = G(K(φ));α_j in E

よって、

• α::K*G⇒F:C→E

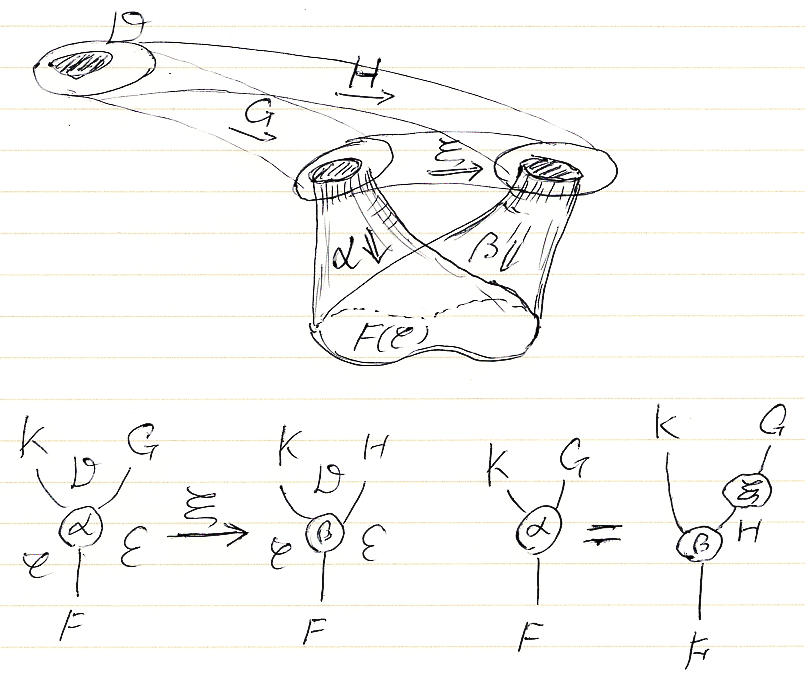
柱に関する状況をまとめて絵に描くと：

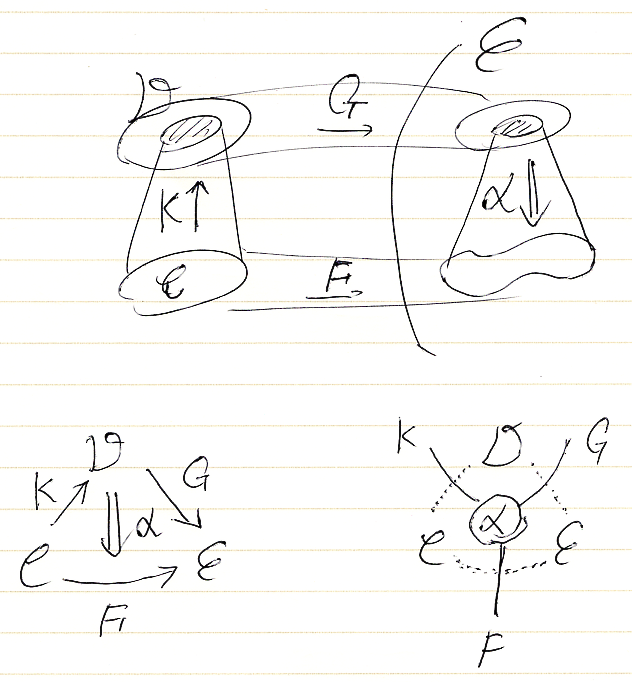
上段は、写実的(?)な絵をちょっと雑に描いたものです。ここに登場する圏C, D, E、関手K, F, G、自然変換αをペースティング図にすると下段の左です。ペースティング図のポアンカレ双対を取れば下段右のストリング図が得られます。ストリング図に、ポアンカレ双対に移る前のK, F, Gの痕跡を点線で描いています（単に説明用で実際は不要）。

柱のストリング図は、「カン拡張における上下左右： 入門の前に整理すべきこと」で紹介した「{左 | 右}{拡張 | 持ち上げ}」カルテットのなかの右拡張の絵になっています。柱は（カンとは限らない）右拡張と同じ概念なのです。

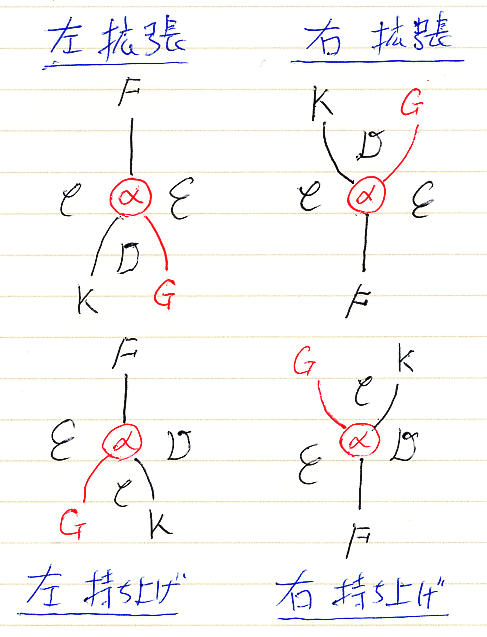
底面を固定した柱の圏

柱を考える際に、柱の形状を最初に決めます。柱の形状は形状関手 K:C→D で決定されるので、形状を決めるとはKを選ぶことです。選んだKに対して様々な柱を考えますが、底面Fは固定して考えることが多いです。カン拡張の議論でも、底面Fは固定します。

底面Fを固定して余底面を色々と動かすのは次のような感じです。

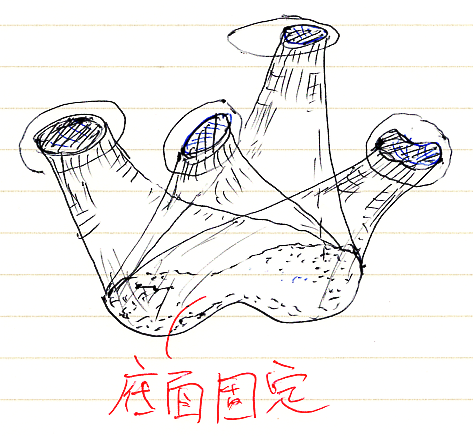
底面Fと余底面Gの両方を固定しても、柱体変換αの多様性があるので、FとGを繋ぐ柱はイッパイあるかも知れません。

固定したF（Kはその前に固定している）に対する柱は、余底面（の変換）を与えるGと、柱体変換（自然変換）αを組みにした(G, α)で記述できます。この書き方をするとき、G:D→E, α::K*G⇒F:C→E であることは暗黙の前提になります。

さて、底面がF（固定）である柱の全体を圏にしましょう。この圏（まだ出来てないが）をCyl_Fとします。Cyl_Fの対象は柱です。Cyl_Fの射として、柱のあいだの準同型（homomorphism between cylinders）を考えます。柱のあいだの準同型の定義は、錐のあいだの準同型を参考にします。

底面がFである2つの錐(X, α)と(Y, β)があるとき（X, Yは頂点、α, βは錐体変換）、(X, α)から(Y, β)への準同型は、f:X→Y というEの射で、f;β = α を満たすものです。f;β = α の正確な意味は：

• ∀i∈|C|. f;β_i = α_i

錐のあいだの準同型（Cone_Fの射）は、頂点のあいだの射fで、fによるβの引き戻しがαに一致するものでした。

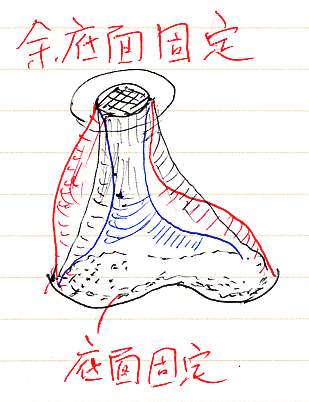
柱でも同じように考えて、(G, α)から(H, β)への準同型は、柱の余底面のあいだの射ξで、ξによるβの引き戻しがαに一致するものとしましょう。

2つの余底面は、関手 G, H:D→E で与えられるので、余底面のあいだの射は、自然変換 ξ::G⇒H:D→E です。このξと β::K*H⇒F:C→E は直接は縦結合できないので、K*ξによりβを引き戻します。つまり、次が成立するとき、ξを (G, α)→(H, β) の準同型と考えます。

• (K*ξ);β = α

柱(G, α)の恒等射は、恒等自然変換 ID_G:G⇒G:D→E とします。恒等射の左単位律／右単位律は明らかでしょう。

J:D→E, γ::K*J⇒F:C→D を組にした(J, γ)を第三の柱とします。ξ:(G, α)→(H, β), τ:(H, β)→(J, γ) in Cyl_F とは次のことです。

• ξ::G⇒H:D→E where (K*ξ);β = α
• τ::H⇒J:D→E where (K*τ);γ = β

自然変換の縦結合 (ξ;τ)::G⇒J:D→E が、Cyl_Fの射としての結合 (ξ;τ):(G, α)→(J, γ) を与え、結合律を満たすことは簡単な計算で分かります*3。

以上により、底面がFである柱の圏〈category of cylinders〉Cyl_Fが定義できました。

おわりに

形状関手 K:C→D をまず決め、Kで定義される形状に対して底面Fを固定した柱の圏Cyl_Fを構成しました。この圏は、カン拡張の言葉を使えば、（カンとは限らない）右拡張からなる圏と同じものです。FのKに沿った右カン拡張は、圏Cyl_Fの終対象です。右カン拡張＝終柱 と言えます。柱の双対（余柱）で同様に考えれば、左カン拡張が得られます。

カン拡張の形式的な定義は、ペースティング図またはストリング図で記述できます。しかし、なかなか実感が得られないので、“写実的”な絵を描いてみました。この絵では、錐と柱の類似性が分かりやすいので、「極限＝終錐」の一般化として「右カン拡張＝終柱」を捉えやすいと思います。多少は実感が増したでしょうか。

*1:結び目の同型性の判定が困難なことを考えると、これは本質的に難しい事なんでしょう。

*2:形状側の柱は、写像柱と似ているので、関手柱と呼んでもいいかも知れません。

*3:「圏論の随伴をちゃんと抑えよう： お絵描き完全解説」で説明した絵を使うといいと思います。