何の必然性もなく命名された「左」「右」を憶えるのは大変です。
「ガーッ! また左と右が。カン拡張」より:
以前、「カン拡張における上下左右: 入門の前に整理すべきこと」というけっこう長い記事を書いたにもかかわらず、 -- にもかかわらずですね、カン拡張の左と右の定義を忘れた。どっちが左でどっちが右か分からなくなった。ハァ(ため息)。
で、「随伴の左右とカン拡張の左右が一致するので、それを手がかりに憶える」ことにしました。が、それでも「あれっ? どっちだっけ?」となります。ダメだ、もう。左右じゃなくて、右だけ覚えよう、右だけ。右を覚えれば、「右じゃないほうが左」とわかるから。$`\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\op}{\mathrm{op}}
\newcommand{\hyp}{\text{-}}
\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\In}{\text{ in } }
\newcommand{\dimU}[2]{{#1}\!\updownarrow^{#2}}
`$
内容:
右カン拡張とラムダ計算
まず、さすがに次は忘れない。
| $`\mrm{Left}`$ | $`\mrm{Center}`$ | $`\mrm{Right}`$ |
KanのKを L, C, R に置き換えて、取り除いたKを下付きにすると:
| $`\mrm{Lan}_K`$ | $`\mrm{Can}_K`$ | $`\mrm{Ran}_K`$ |
Kは形状関手(後述)の「ケ」とも憶えられます。
$`\mrm{Can}_K`$ は、関手 $`K`$ のプレ結合引き戻しです。他の随伴トリプル(Σ-Δ-Π とか ∃-◇-∀)を思い起こせば、センター〈Center〉がプレ結合引き戻しなのは大丈夫そうです。
右の $`\mrm{Ran}`$ は、センターの $`\mrm{Can}`$ の右随伴なので、次が成立します。
$`\quad \mrm{Can}_K \dashv \mrm{Ran}_K`$
随伴のホムセット同型は次の形です。
$`\quad ?(\mrm{Can}_K(\hyp), \hyp) \cong \;?(\hyp, \mrm{Ran}_K(\hyp))`$
疑問符のところには関手圏が入ります。どんな関手圏だったか思い出すには、ラムダ計算のカリー化/反カリー化と類似の次の絵を描きます。
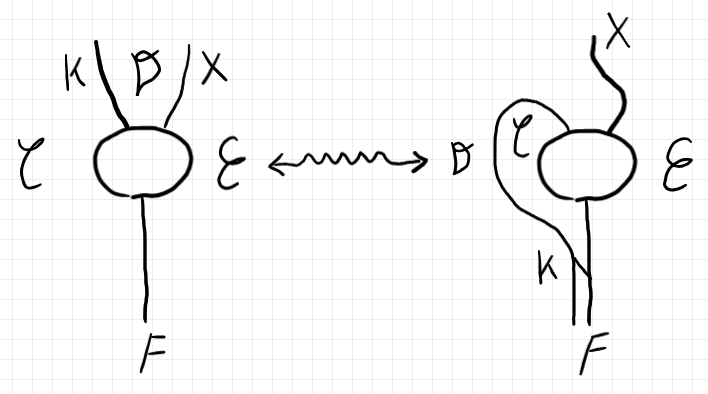
この絵を見ながら次のように書き出します。
$`\quad [\cat{C}, \cat{E}](\mrm{Can}_K(X), F) \cong [\cat{D},\cat{E}](X, \mrm{Ran}_K(F) )`$
これは次のようにも書けます。$`\mrm{Ran}_K(F) = {^K F}`$ という記法を使います。
$`\quad [\cat{C}, \cat{E}](K * X, F) \cong [\cat{D},\cat{E}](X, {^K F} )`$
絵からはラムダ計算との類似性がただよっています。「右カン拡張はラムダ計算の仲間だろう」とは次の古い記事でも書いています。
この類似性をハッキリさせるために、モノイド圏 $`\cat{M}`$ を特殊な2-圏とみなします。ただひとつの対象 $`\bullet`$ を持つ2-圏がモノイド圏 $`\cat{M}`$ だとします。そして、次の対応を考えます。
| $`{\bf CAT}`$ | $`\cat{M}`$ |
| $`\cat{C}, \cat{D}, \cat{E}`$ | $`\bullet`$ |
| $`*`$ | $`\otimes`$ |
| $`K:\cat{C} \to \cat{D}`$ | $`K:\bullet \to \bullet`$ |
| $`F:\cat{C} \to \cat{E}`$ | $`F:\bullet \to \bullet`$ |
| $`X:\cat{D} \to \cat{E}`$ | $`X:\bullet \to \bullet`$ |
2-圏において、随伴のホムセット同型を書いてみます。
$`\quad {\bf CAT}(\cat{C}, \cat{E})(K * X, F) \cong {\bf CAT}(\cat{D}, \cat{E})(X, {^K F})\\
\quad \cat{M}(\bullet, \bullet)(K\otimes X, F) \cong \cat{M}(\bullet, \bullet)(X, {^K F})
`$
これで、類似性の由来がわかります。
インデックス付き圏として
もうひとつ、Δ-Π 随伴との対応も見ておきます。$`P:\cat{J}^\op \to {\bf CAT}`$ をインデックス付き圏として、
$`\quad K:C \to D \In \cat{J}`$
がベース圏〈インデキシング圏〉 $`\cat{J}`$ 内の射とします。$`K`$ で誘導される引き戻し関手〈リダクト関手〉
$`\quad \Delta_K = K^* = P[K] \;: P[D] \to P[C] \In {\bf CAT}`$
に右随伴があれば、それが $`\Pi_K`$ です。
$`\quad \Delta_K : P[D] \to P[C] \In {\bf CAT}\\
\quad \Pi_K : P[C] \to P[D] \In {\bf CAT}\\
\qquad \Delta_K \dashv \Pi_K
`$
右カン拡張をこのフレームワークで記述してみます。小さい圏の1-圏 $`\dimU{\bf Cat}{1}`$ とします。2-圏の2-射を捨てた1-圏を $`\dimU{\cat{K}}{1}`$ と書いています。この書き方については「圏の次元調整」を見てください。
$`\cat{E}`$ を局所小圏として、$`\dimU{\bf Cat}{1}`$ をベース圏とするインデックス付き圏 $`P`$ を次のように定義します。
$`\quad P[\hyp] := [\hyp, \cat{E}]`$
もう少し詳しく書くと:
$`\text{For }\cat{C} \in |\dimU{\bf Cat}{1}|\\
\quad P[\cat{C}] := [\cat{C}, \cat{E}] \;\in |{\bf CAT}|\\
\text{For }K: \cat{C} \to \cat{D} \In \dimU{\bf Cat}{1}\\
\quad P[K] := K^* = (K * \hyp) \;: [\cat{D}, \cat{E}] \to [\cat{C}, \cat{E}] \In {\bf CAT}
`$
このセッティングで、
$`\quad \Delta_K = K^* = P[K] \;: P[\cat{D}] \to P[\cat{C}] \In {\bf CAT}`$
に右随伴があれば、それが $`\Pi_K`$ です。
$`\quad \Delta_K : [\cat{D}, \cat{E}] \to [\cat{C}, \cat{E}] \In {\bf CAT}\\
\quad \Pi_K : [\cat{C}, \cat{E}] \to [\cat{D}, \cat{E}] \In {\bf CAT}\\
\qquad \Delta_K \dashv \Pi_K
`$
これは右カン拡張 $`\mrm{Ran}_K`$ の定義にほかなりません。
$`\qquad \Delta_K \dashv \mrm{Ran}_K`$
関連する関手・自然変換の名前
カン拡張が憶えにくいのは、構造としての構成素に役割り名が付いてないことも原因です。「カン拡張のために、柱の絵を描く」において、柱のイメージからカン拡張に出現する関手・自然変換に名前〈役割り名〉を付けておきました。関連する絵を再掲します。
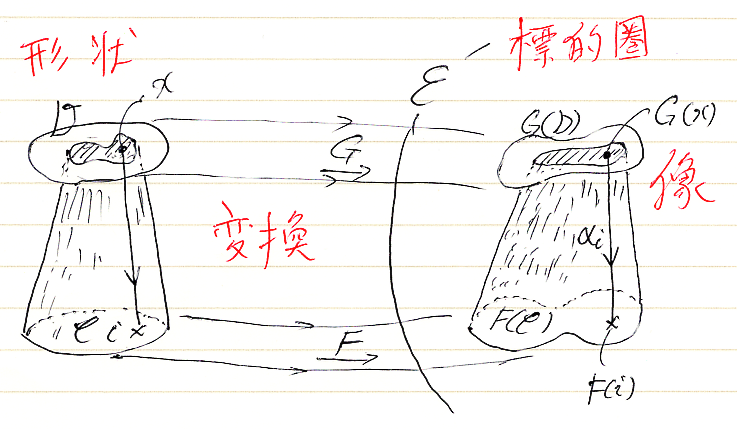
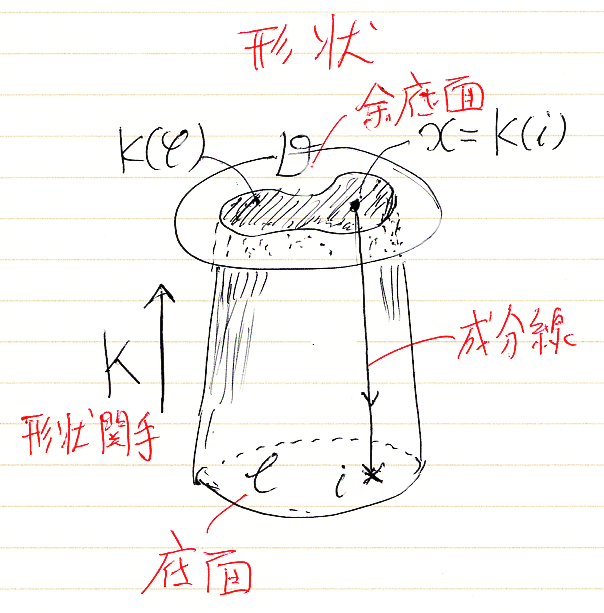
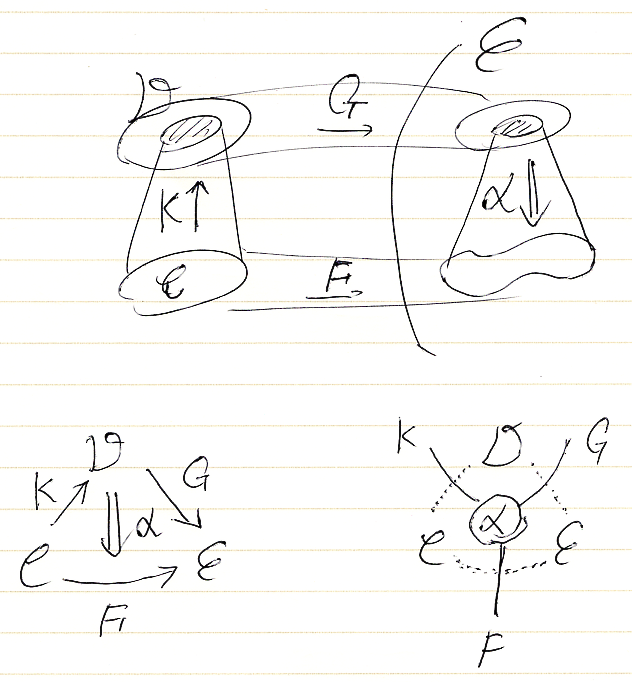
過去記事では、関手のことも「変換」と呼んでいるところがありますが、紛らわしいので自然変換だけを「変換」と呼ぶことにします。
- 形状関手: $`K:\cat{C} \to \cat{D}`$
- 標的圏〈ターゲット圏〉: $`\cat{E}`$
- 底面関手: $`F:\cat{C}\to \cat{E}`$
- 余底面関手: $`G:\cat{D}\to \cat{E}`$
- 柱体変換: $`\alpha :: K*G \Rightarrow F : \cat{C} \to \cat{E}`$
例えば、ホムセット $`[\cat{C}, \cat{E}](K*X, F)`$ の要素は、形状関手 $`K`$ 、底面関手 $`F`$ 、余底面関手 $`X`$ の柱体変換の集合と呼べます。