自然変換の計算法 DOTN二号 - 檜山正幸のキマイラ飼育記 (はてなBlog)

DOTNとは、図式順テキスト記法（Diagrammatic-Order Text Notation）のアクロニムで、はじめてそれについて書き記したのは次の記事かな（2006年）。それ以前から使ってましたけどね。

http://www.chimaira.org/docs/DOTN.htm

このダイアリー内でも：

最近、DOTNで使う記号を少し変えました。ピエル=ルイ・キュリア（Pierre-Louis Curien）の図式法のアイデアを取り入れたのです。キュリアの絵算については：

キュリアの方法で注目すべき点は、圏の射を「自然変換ともみなす」ことです。これにより、圏の対象、射、圏それ自体、関手、自然変換を全部混ぜた計算が、統一的な絵図で行えるようになります。この発想は、DOTNとの相性も大変よいものです。

DOTNは、ナプキンペーパーやホワイトボード上で、できるだけ手早く自然変換の計算をすることを目的とする記法で、次の方針に基づきます。

イタリックやボールドなどのフォントによる識別は使わない。手書きやテキストエディタで書くのが困難なので。
同様な理由で、上付き・下付きの添字も使わない。
ギリシャ文字（α、βなど）とアスキーの範囲内の文字を使う。
絵図と直接的に対応する記法とする。絵図は、上から下、左から右の順で描く。テキスト記法も左から右。
できるだけ短く書けるようにする。

http://www.chimaira.org/docs/DOTN.htm のときからずっと変わってない書き方の規則は：

圏の対象は、a, b, c など。英小文字、始めのほうと終わりのほう。
圏の射は、f, g など。英小文字、中間のあたり。
圏は、A, B, C, D など。英大文字、始めのほう。
関手は、F, G など。英大文字、中間のあたり。
自然変換は、α, β などギリシャ文字小文字。
射fとgのこの順での結合は f;g と書く。
対象aの恒等射は a^ と書く。

圏の射に対する f:a→b とか、自然変換に対する α::F⇒G:C→D などの書き方も最初から変わってません。

圏の対象が小文字であることに違和感をおぼえる人は（慣れの問題ですが）、圏は A, B, C など、圏の対象は X, Y, Z などにしてもいいと思います。

最近、キュリアの方法を加味して整理したのは、中置二項演算子記号です。一律に次のように約束します。

縦結合は「;」（セミコロン）を使う。射の結合は縦結合なので、従来と変わらない。
横結合は「*」（アスタリスク、スター）を使う。関手の通常の結合は横結合なので、F;G ではなくて F*G となる。
適用は「.」（ドット）を使う。a.F、f.F、a.α、f.α のいずれも使う。

射の結合は f;g ですが、関手の結合が F*G になるのが大きな変化です。これにより、絵算との対応が非常にストレートになります。なにしろ、縦（上下方向）か横（左右方向）かの区別と完全に対応するので。射の結合と関手の結合が（方向的に）異なった概念であることに慣れるには少し時間がかかるかも知れません（僕もやっと慣れてきた）。

「格上げ」に使う2つの後置単項演算子記号も定義します。

恒等を作るには「^」（サーカムフレックス、ハット）を使う。a^（恒等射）、A^（恒等関手）、F^（恒等自然変換）のいずれも使う。
対象→関手、射→自然変換の格上げには「~」（チルダ）を使う。a~、f~ は、単位圏1からの関手と自然変換になる。

チルダ演算子の導入は、キュリアの方法からの影響によります。「^」「~」を使って格上げすると、適用「.」は横結合「*」に変わります。このことから、適用と横結合が類似している（同一視も可能な）ことが分かります。

計算を実際に遂行する上での大原則は交替律（interchange law）です。キュリアはグッドモンの規則（the Godement's rule）と呼んでいます。エックマン／ヒルトン論法（The Eckman-Hilton argument）の根拠となっているので、エックマン／ヒルトンの法則とか呼ぶ人もいるようです。なお、自然変換の横結合（horizontal composition）をグッドモン積（Godement product）とも言うようです。

交替律に対する一番直感に訴える呼び名は「エレベーター規則」でしょう。キュリアによれば、交替律は a "physical" translation を持っていて、"moving elevators" up and down. と述べることができる、と。似たような表現で垂直ずらし（vertical shift/sliding）と言っていた人もいたと思います。

呼び名はともかくとして、交替律は、絵図の上ではほとんど自明に見えるにも関わらずものすごく強力な計算法則です。特に、キュリア流に「対象、射、圏、関手、自然変換を全部混ぜて」一律に交替律を適用すると、自然変換の計算の複雑さが消えてしまいます。

できればそのうち、具体的な計算例により、DOTN二号（最近新しくしたDOTN）を紹介したいと思います。

[追記]

とりあえず、面白いなーと思える簡単な例を1つ。違和感を少なくするため、圏の対象は小文字じゃなくて X,Y とかにします。添字を使わないので、自然変換αの成分は α_X じゃなくて X.α と書きます。α::F⇒G:C→D が自然変換であることは、f:X→Y in C に対して次の図式が圏D内で可換になることでした。

 X.F -(X.α)->X.G
  |            |
(f.F)        (f.G)
  |            |
  v            v
 Y.F -(Y.α)->Y.G

この図式の、X.FからY.Gに至る対角線は、可換性から一意に決まるので、それを f.α と書くことにします。すると；

(f.F);(Y.α) = f.α
f.α = (X.α);(f.G)
(f.F);(Y.α) = (X.α);(f.G)

です。「適用と横結合が類似している（同一視も可能）」なので、これは（適度な記号の乱用のもとで）次のように解釈してもかまいません。

(f*F);(Y*α) = f*α
f*α = (X*α);(f*G)
(f*F);(Y*α) = (X*α);(f*G)

これは交替律であり、下図のような“エレベーター状態”の同値性の主張です。

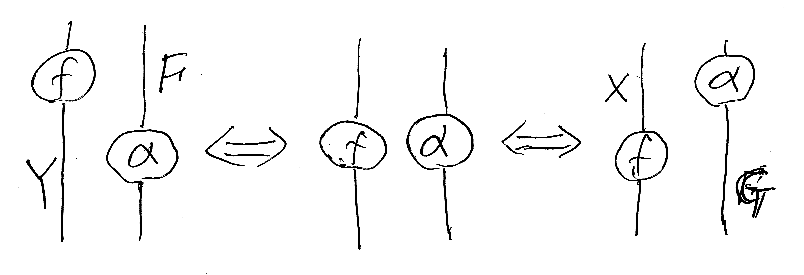
[/追記]