距離空間や一般の位相空間を勉強中のN君ですが、「任意の」や「存在する」の扱いには苦労しているようです。特に、「前提にある存在命題の使い方が分からない」と。うん、難しいですよね。「習うより慣れろ」と言われても、そう簡単に慣れるもんじゃないです。

∀と∃をちゃんと使うには、実用的なテンプレートを意識して、当座はそのテンプレートに沿って命題や証明を書いたほうがいいと思います。そのようなテンプレート、特に存在記号のためのテンプレートと、その使い方を紹介します。
内容:
関連する記事:
- 論理の全称記号∀も存在記号∃もちゃんと使えるようになろう
- 全称記号と存在記号に関する推論規則
- 全称命題を準備するボックスを使ってみよう: 最小元の存在
- 背理法も使ってみる: 最大元の非存在
- おわりに
はじめに
「イプシロン-デルタ論法はなぜ難しいのか? どうしたら分かるのか? 分かる必要があるのか?」に、次のように書きました。
イプシロン-デルタ論法のために必要なスキルとして、次が要求されています。
- 点の集合だけでなく、集合の集合を扱うスキル(あるいは慣れ)。
- 「任意の」「存在する」という言葉を含む論理的な表現を扱うスキル(あるいは慣れ)。
これはもちろん、イプシロン-デルタ論法だけではなくて、空間やら構造やらを扱うときは常に必要になります。
「任意の」「存在する」の使い方は、述語論理の推論規則によって統制されているのですが、あまり分かりやすいものではありません。次の2つの記事で詳しく分析しています。が、ちょっと詳し過ぎたかも知れません。
命題の記述や証明がうまく出来ないと「論理的に考えていないから」と思いがちですが、そうとも限りません。単に技術的な問題、つまりノウハウが不足しているだけかもしれません。特に、∀と∃の取り扱いはノウハウが必要です。この記事は、ノウハウと事例の提供を目的にしています。
例題と予備知識
今回例題に使うのは、自然数の順序関係(大小順序関係)です。自然数の全体を N = {0, 1, 2, ...} とします。0も自然数に入れている点に注意してください。自然数の演算としては、足し算しか考えません。足し算は次の法則を満たします。
- (a + b) + c = a + (b + c) ---(結合律)
- a + b = b + a ---(交換律)
- a + 0 = a ---(ゼロの中立性)
他にも必要な法則(公理)がありますが、必要になった時点で導入します。
いま述べた結合律などの法則は、実は全称記号〈全称限量子 | 全称量化子 | universal quantifier〉∀が付いています。
- ∀a, b, c.( (a + b) + c = a + (b + c) )
法則には常に全称記号が付くので、「常に付くなら常に省略してもいいだろう」と省略されます。
変数 a, b, c は、今の場合は自然数を表します。変数の変域(変数の型)を明示するなら、
- ∀a, b, c∈N.( (a + b) + c = a + (b + c) )
です。∀a, b, c∈N という書き方も略記で、ちゃんと書くなら:
- ∀a∈N.∀b∈N.∀c∈N.( (a + b) + c = a + (b + c) )
単に命題をポンと出しても、それの真偽は不明です。「この命題は真だぞ」という主張を伴うなら、「真だぞ」を意味する判断〈judgement〉記号 '|-' を添えたほうが確実です*1。
- |- ∀a∈N.b∈N.c∈N.( (a + b) + c = a + (b + c) )
まーしかし、さすがに面倒くさいので、(a + b) + c = a + (b + c) とだけ書いて、結合律の提示とするのです。「毎回、真面目に律儀に書け」と言う気は無いですが、省略、省略、省略のあげくに簡潔な書き方をしていることは意識すべきです。省略された情報は文脈から補いますが、文脈に頼りすぎるとコミュニケーションが失敗します*2。明示的に書くか、暗黙の前提で済ますかは、よくよく考える必要があります。
「式」という言葉は多義・曖昧過ぎるので、この記事では「命題〈proposition〉」と「項〈term〉」を使います。命題は真偽判定が可能(だと想定されるよう)な文、項はなんかのモノ(例えば自然数)を表す(と想定される)記号表現です。(ただし、単項式/多項式の意味の項とは違います。単項式/多項式の項はサマンド〈summand〉*3のことです。)x や x + 1 は項で、∀x.(x = x + 1) は命題です。
命題を一般的に表すために P, Q などを使い、項を一般的に表すために s, t などを使います。これらはメタ変数なので、書体を変えるのが望ましいのですが、普通のローマン体で書きます。「普通の変数(今回は自然数を表す変数)か? メタ変数(命題や項を一般的に表す変数)なのか?」は、“文脈で”判断してください。
自然数の大小順序と証明の例: 反射律
自然数の大小は、足し算とは独立に理解されるでしょう。例えば、足し算が出来ない小さな子供でも、個数の大小は認識できるかもしれません。しかしここでは、足し算ありきで、大小の順序関係は足し算により定義される、と考えましょう。
- x ≦ y :⇔ ∃z.(x + z = y) --(大小順序の定義)
':⇔'は、定義であることを強調した論理的同値です。全称記号や変数の型(所属する集合)までちゃんと書けば:
- ∀x, y∈N(x ≦ y ⇔ ∃z∈N.(x + z = y)) --(大小順序の定義)
いま定義した x ≦ y が、ちゃんと順序関係になっているか、確認します。「x ≦ y が順序関係である」とは次が成立することです。
- x ≦ x ---(反射律)
- x ≦ y, y ≦ x ⇒ x = y ---(反対称律)
- x ≦ y, y ≦ z ⇒ x ≦ z ---(推移律)
順に証明を付けていきましょう。
まず反射律に対して次の証明要求を考えます。
- Γ |-? ∀x∈N.(x ≦ x)
証明要求とは、その名の通り「この命題を証明してください」という依頼や指示のことです。'|-?'の左側が証明のときに使っていい前提で、'|-?'の右側が証明のターゲット命題(目的とする命題)です。大文字ガンマ'Γ'は、諸々の前提をまとめて書くときに使います。
証明要求について詳しくは、次の記事とそこからのリンク先を参照してください。
上記記事には、証明要求の変形についても書いてあり、それを証明の“お膳立て”と呼んでいます。次はお膳立ての例です。
Γ |-? ∀x∈N.(x ≦ x) ----------------------[全称の変形] Γ, x∈N |-? x ≦ x
変形後の証明要求は次のようにして証明(契約が履行)されます。
証明要求: Γ, x∈N |-? x ≦ x x + 0 = x ---(1) --[∃導入 0:←z] ∃z.(x + z = x) ---(2) // 大小順序の定義より x ≦ x ---(3)
こんな短い証明ですが、いつくもの約束が使われています。それらを説明していきます。
- 証明の最後の命題は、証明要求のターゲット命題('|-?'の右側)と同じでなければならない。
上の例では、最後の命題(番号は(3))と、証明要求のターゲット命題は、どちらも x ≦ x ですからいいですね。
- 証明内に出現するすべての命題は、その根拠がハッキリしてなくてはならない。
証明内に出現する命題には (1), (2), (3)と番号がふってあります。(1), (2), (3)すべてに根拠が必要ですが、根拠記述には次の3つの方法を適宜使い分けています。
- 根拠が明らかと思える場合は、特に何も書かない(省略)。
- 使っている推論規則を推論バー形式で書く。
- コメントとして短いヒントを書く。
(1)の x + 0 = 0 は、証明要求の前提('|-?'の左側)から容易に推論できるので、根拠は何も書いてません。(1)から(2)は、「∃導入」と呼ばれる推論規則を使っています。∃導入の一般的な形は次のようです。
P --------------[∃導入 t:←v] ∃v.P[t:←v]
ここで、Pは何らかの命題(Pは命題を表すメタ変数)です。P[t:←t] は、Pのなかに含まれる項t(tは項を表すメタ変数)を、変数v(vは変数を表すメタ変数)で置き換えたものです。今の具体例では、
x + 0 = x ------------------[∃導入 0:←z] ∃z.(x + z = x)
命題 x + 0 = x のなかに含まれる項 0 (0も項です)を、変数(具体的な実際の変数)zで置き換えた x + z = x に存在限量子 ∃z を付けて ∃z.(x + z = x) を出しています。
なお、推論バーのバー(横棒)の長さを調整するのがイヤになったので、長さは調整しません! ハイフン2,3個並べてバーを表現します。
先の具体例の(2)から(3)はコメントでヒントを書いています。
∃z.(x + z = x) ---(2) // 大小順序の定義より x ≦ x ---(3)
大小順序の定義は、x ≦ y ⇔ ∃z.(x + z = y) だったので、yをxに置き換えると、x ≦ x ⇔ ∃z.(x + z = x) 、これと(2)から、(3)が出るわけです。詳細に推論を積み重ねなくても、コメントで十分でしょう。
存在命題を料理するボックスを使ってみよう: 反対称律
では次に、反対称律の証明にいきましょう。
- x ≦ y, y ≦ x ⇒ x = y ---(反対称律)
この命題をちゃんと書けば:
- ∀x, y∈N(x ≦ y ∧ y ≦ x ⇒ x = y)
その証明要求は、
- Γ |-? ∀x, y∈N(x ≦ y ∧ y ≦ x ⇒ x = y)
変形して、
- Γ, (x, y∈N) |-? x ≦ y ∧ y ≦ x ⇒ x = y
証明要求の左側(前提)に出現する (x, y∈N) は、一種の変数宣言だと思ってください。もう少し変形(お膳立て)しておきましょう。
Γ, (x, y∈N) |-? x ≦ y ∧ y ≦ x ⇒ x = y ----------------------------------------------[含意の変形] Γ, (x, y∈N), (x ≦ y ∧ y ≦ x) |-? x = y ----------------------------------------------[前提の連言を分解] Γ, (x, y∈N), x ≦ y, y ≦ x |-? x = y
さらに、x ≦ y と y ≦ x を、大小順序の定義により書き換えれば:
- Γ, (x, y∈N), ∃z∈N.(x + z = y), ∃z∈N.(y + z = x) |-? x = y
これでお膳立ては終わり。実際の証明にかかります。
前提(証明のときに使ってよい命題達)に∃が入っているので、これは「前提にある存在命題の使い方」を練習するチャンスです。存在命題を使うときは、専用のボックスを使いましょう。
ボックスは、「全称記号の導入規則について考える」と「存在記号の除去規則について考える」で説明したもので、次のようなものです。
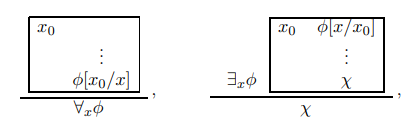
この絵がピンと来なくてもいいです。∀や∃の扱いでは、証明の一部分を囲むボックスが必要だ、と認識してください。存在記号∃の除去〈elimination〉に使うボックスは次のようです。
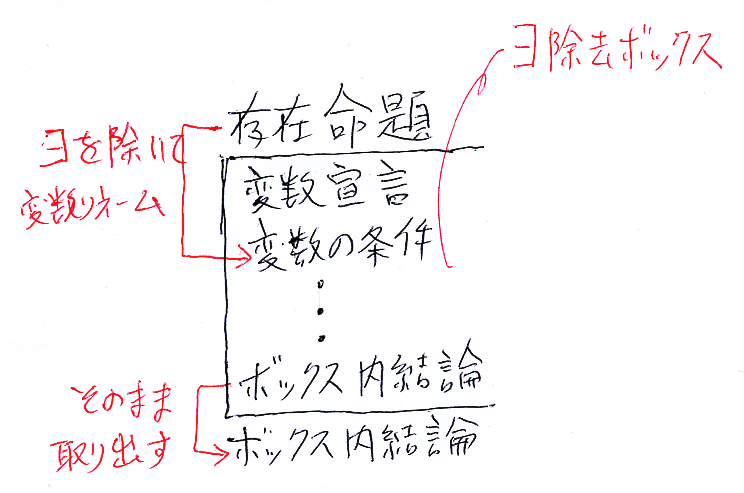
さっそく実際に使いたいのですが、テキストで書いた証明内でボックスをリアルに描くのは非常にめんどくさいので、次の記法を使います。
●存在命題 BEGIN ∃除去 変数宣言 変数の条件 : : ボックス内結論 END ボックス内結論
BEGIN/ENDとインデントを使います。黒丸'●'は、存在命題が目立つようにです。この形式で反対称律の証明を行います。説明は後でします。
証明要求: Γ, (x, y∈N), ∃z∈N.(x + z = y), ∃z∈N.(y + z = x)
|-? x = y
●∃z∈N.(x + z = y)
BEGIN ∃除去
a∈N
x + a = y ---(1)
●∃z∈N.(y + z = x)
BEGIN ∃除去
b∈N
y + b = x ---(2)
// (1)と(2)から
(x + a) + b = x
// 結合律から
x + (a + b) = x
// ゼロの中立性から
x + (a + b) = x + 0
// 消約律(後述)から
a + b = 0
// ゼロ和自由性(後述)から
a = 0 ∧ b = 0
// 連言の左を取り出して
a = 0 ---(3)
// (1)と(3)から
x = y
END
x = y
END
x = y
証明のなかで、まだ触れてない法則が出てくるので、それを述べておきます。消約律 〈cancellation property | cancellation law〉は次の形の法則です。
- a + x = a + y ⇒ x = y
ちゃんと書けば:
- ∀a, x, y∈N.(a + x = a + y ⇒ x = y)
ゼロ和自由性〈zerosumfree property〉は次の形。
- a + b = 0 ⇒ a = 0 ∧ b = 0
ちゃんと書けば:
- ∀a, b∈N.(a + b = 0 ⇒ a = 0 ∧ b = 0)
これらの法則については次の記事で述べています。興味があればどうぞ。
さて、問題の存在命題の扱い方ですが、この具体例では、∃除去ボックスを入れ子にして使っています。ほとんどの証明は内側の∃除去ボックスで遂行されているので、内側の∃除去ボックスだけ取り出します。
●∃z∈N.(y + z = x)
BEGIN ∃除去
b∈N
y + b = x ---(2)
:
:
x = y
END
x = y
存在命題 ∃z∈N.(y + z = x) をこの∃除去ボックス内で料理します。ボックスの1行目は、ボックス内だけで使う変数の宣言です。この変数*4の名前の選び方は次のとおり。
- ボックス内から、ボックス外の変数を参照することがあるので、外部の変数と違う名前を選ぶ。これは守るべし!
- 存在命題の束縛変数とは違う名前を選んだほうが事情がハッキリする。これは、あまり守られてないし、破っても実害はない。が、最初のうちは混乱を防ぐために違う名前を推奨。
上の具体例では、
- ボックスの外側で、x, y, aが既に使われているので、これと同じ名前はダメ。
- 存在命題の束縛変数がzだから、混乱を避ける意味でzと別な名前にする。
で、ボックス内で使う変数にbを選んでいます。変数名の衝突や、紛らわしい名前による混乱を避けるため、変数名の選択法は重要なスキルです。にも関わらず、明示的に述べられず、トレーニングの機会も少ないのは困ったことです。
∃除去ボックスの2行目は、今導入したボックス内変数(具体的にはb)に関する条件です。もとの存在命題の束縛変数(具体的にはz)を、ボックス内変数で置き換えた命題を書きます。y + z = x のzをbに置き換えるので、y + b = x となります。
あとは、ボックス内で証明を遂行して結論を出します。ボックス内の結論には、変数宣言で導入したボックス内変数が入っていてはダメです。ただし、束縛変数なら話が別です。例えば、∀b∈N.(...) のようにbを使うなら問題ありません。とはいえ、これも混乱のもとなので、自由変数(ボックス内変数も自由変数)と、∀, ∃の束縛変数は別な名前を使いましょう。慣れた人は同じ変数を平気で使い回す*5ので、それがまた初心者を困惑させたりします。
- 慣れるまでは、自由変数と束縛変数に、別な名前を使うことを推奨。
ボックス内結論は、ボックスの外に取り出します。同じ命題を2回書くので冗長ですが、∃除去ボックスのスコープから結論をエクスポートしたことを確認する意味で、2回書きましょう*6。結論がボックス外に取り出せるために、ボックス内変数bが入っていてはダメなのです。
以上に述べたことが、前提である存在命題の使い方の決まり文句=テンプレートです。律儀に守ると、かなり冗長になりますが、慣れるまではテンプレート通りに書きましょう。
もっとボックスを使ってみよう: 推移律
推移律の証明もやってみましょう。証明要求は、次のようです。
- Γ |-? ∀x, y, z∈N.(x ≦ y ∧ y ≦ z ⇒ x ≦ z)
前節と同じ要領で証明要求を変形すれば:
- Γ, (x, y, z∈N), ∃z∈N.(x + z = y), ∃w∈N.(y + w = z) |-? ∃w∈N.(x + w = z)
(わざとに)自由変数と束縛変数を同じ名前にしているので、注意してください。紛らわしいだけで間違いではありません。この設定で推移律を証明してみましょう。
証明要求: Γ, (x, y, z∈N), ∃z∈N.(x + z = y), ∃w∈N.(y + w = z)
|-? ∃w∈N.(x + w = z)
●∃z∈N.(x + z = y)
BEGIN ∃除去
a∈N
x + a = y ---(1)
●∃w∈N.(y + w = z)
BEGIN ∃除去
b∈N
y + b = z ---(2)
// (1), (2)より
(x + a) + b = z
// 結合律より
x + (a + b) = z
--[∃導入 (a + b):←w]
∃w∈N.(x + w = z)
END
∃w∈N.(x + w = z)
END
∃w∈N.(x + w = z)
前節とほとんど同じなので、説明は要らないですね。
注意すべきは、やはり変数の使い方です。あえて、同名の自由変数と束縛変数を使っています。自由変数と同名の束縛変数を使うのはかまいません(でも、ときに混乱をまねきます)。異なる命題で同じ束縛変数を使うのも問題ありません(でも、ときに混乱をまねきます)。上の証明内に現れる変数は:
- 自由変数 x, y, z(前提で宣言されている)
- 束縛変数z(前提の命題)
- 束縛変数w(前提の命題)
- 自由変数a(外側の∃除去ボックスで宣言されている)
- 自由変数b(内側の∃除去ボックスで宣言されている)
- 束縛変数w(ターゲット命題、内側の∃除去ボックス内の∃導入で導入)
こういった変数の名前と型(変域、所属する集合)、そしてスコープ(有効範囲)の管理がとても大事です。変数に名前・型・スコープがあること、スコープは入れ子のブロック構造になること -- このへんはプログラミング言語と同じです。自然言語で適切に表現するのは難しいです。
だから、機械可読で、機械(ソフトウェア)でチェック可能な人工言語で証明を書くほうがいいと僕は思うのですが、残念ながら、広く実用に耐える証明支援系は存在しません。
「こうすればCoqに入門できそうだ (誰も書かないCoq入門以前 5)」:
Coqに関する情報はけっこう多いのですが、ゲームとして遊び始めるための良い説明は少ないです。多くの人が入門的な解説を試みてはいますが、Coqの入門的な説明はとても困難だと思います。
「Isabelleについて: 証明支援系は何を目指し、どこへ向かうのか」:
Isabelleが世の趨勢と離れるのか? という話をしてますが、有り体に言えば、もともとIsabelleは独特の文化を持った癖の強い処理系で、利用者は特殊な人々です。証明支援系を使いたくても、Isabelleを避ける人はいるでしょう。僕自身、Isabelleは「ダメだこりゃ」と思った1人です。
僕はほんとに「もったいない」と思っています。システムとコミュニティがこのままだと、せっかく蓄積した膨大なライブラリもあまり活用されないままに朽ちていく懸念さえあります。それはあまりにも「もったいない」。
3次元ビュー、まともなアニメーション機能、5次元以上の正しい計算モデルなどは(ユーザーなら)誰でも欲しいでしょうが、実現するのは何年先でしょうか? このソフトウェアの性格からいって、10年、20年のスパンで進化と成長を見守るべきでしょう。
おわりに
自然数の大小順序だけでも、まだネタはありますし、もう少し練習問題があったほうがいい気もします。全称記号∀に関する説明が不足してるし、∀と∃の関係も述べていません。が、長くなるので今回はこのくらいにしておきます。
論理の教科書には、推論バーの積み重ねで証明が出来るかのごとくに書かれていますが、それだけでは不十分です(「自然演繹はちっとも自然じゃない -- 圏論による再考」参照)。ボックス(ブロック)の入れ子構造と、変数のライフタイム管理も必要です。
とりあえず、∃除去ボックスのテンプレートを使えるようにしましょう。慣れるまでは、変数のスコープに意識を向け、冗長でも律儀に変数をリネームしましょう。
続きがあるよ。
*1:記号'|-'は構文論的な真(公理か証明済み)を主張します。一方、記号'|='は意味論的な真を主張します。
*2:「何言ってるか(書いていあるか)よく分からない」ときは、文脈を共有できてないことが多いです。
*3:サマンドの訳語に「加数」というのがあるようですが、あんまり聞かないですね。
*4:固有変数〈eigenvariable〉、またはパラメータと呼ぶようですが、あまり使われない言葉なので、ボックス内変数にしておきます。
*5:同じ変数の使い回しをしないと、文字が足りなくなってしまうので、実際的には使い回しをせざるを得ない事情があります。
*6:変数水増しオペレーターの効果も考えると、まったく同じ命題を2回書いているのではありません。見た目は同じでも議論域〈domain of discourse〉は変わっています。変数水増しオペレーターについては、「存在記号の除去規則について考える」を参照。