昨日の記事「全称・存在限量子の色々をまとめた絵」に対するオマケのようなものです。が、昨日の記事とは独立に読めます。
空虚な束縛〈vacuous quantification〉の話をします。随伴関手対の観点からの説明です。
内容:
- 空虚な束縛とは
- 随伴ペアとEPペア
- 変数水増しと空虚な束縛
- 射影の逆像と像はEPペア
空虚な束縛とは
Pが、集合X×Y上の述語だとします。構文的には、Pは変数x, yを含む(可能性がある)とします。正確には、意味領域の述語(真偽値をとる関数) P:X×Y→{True, False} と、それを表現する構文領域の存在物である論理式は別物なんですが、ここではあまり区別しないで、同じ記号で表します。「命題」という言葉も、意味領域の述語だったり、構文領域の論理式だったり、文脈で指すものが変わります。
さて、全称命題 ∀x∈X.P(x, y) や存在命題 ∃x∈X.P(x, y) を作ると、変数xは束縛〈bind〉されるので、自由変数はyだけになり、集合Y上の述語となります。限量子(∀か∃)の束縛作用により、述語の領域〈domain of discourse〉が変わります -- 束縛作用とはそういうものです。
Pに変数xが出現してない場合はどうでしょうか。例えば、X = Y = R として、
- P ≡ (y2 = 2)
ここで、'≡'は論理式(構文的表現)として同じことです。構文的な論理式を関数とみなすのに型付きラムダ記法を使うなら、
- P = λ(x, y)∈R×R.(y2 = 2 : {True, False})
冒頭で「あまり区別しない」と言ったのは、論理式としての y2 = 2 と、関数としての λ(x, y)∈R×R.(y2 = 2 : {True, False}) をどちらも同じPで表すよ、という意思表示です。
論理式 P ≡ (y2 = 2) を限量子で束縛すると:
- ∀x∈R.P ≡ ∀x∈R.(y2 = 2)
- ∃x∈R.P ≡ ∃x∈R.(y2 = 2)
形の上では束縛してますが、束縛変数が出現しないので、束縛は無意味にみえます。このような束縛を空虚な束縛〈vacuous quantification〉と呼びます。「述語論理とインデックス付き圏と限量随伴性」では、若干意訳して「無意味限量」と言ってました。
これは名前通り、空虚で無意味に思えますが、実はなかなか面白いものです。空虚な束縛を分析するために、順序集合(むしろプレ順序集合)における随伴性を復習しましょう(次節)。
随伴ペアとEPペア
A = (A, ≦), B = (B, ≦) をプレ順序集合とします。プレ順序'≦'は次を満たします。
- a ≦ a ---(反射律)
- a ≦ b, b ≦ c ⇒ a ≦ c ---(推移律)
写像 f:A→B が単調〈monotone〉だとは、
- a ≦ b ⇒ f(a) ≦ f(b)
であることです。
f:A→B, g:B→A が単調写像だとして、次の条件について考えます。
- ∀a∈A. a = g(f(a))
- ∀a∈A. a ≦ g(f(a))
- ∀b∈B. f(g(b)) = b
- ∀b∈B. f(g(b)) ≦ b
このなかから2つの条件を選んで組み合わせます。まず:
- (∀a∈A. a = g(f(a))) ∧ (∀b∈B. f(g(b)) = b)
このとき、fとgは互いに逆です。fとgは逆ペアと呼んでいいでしょう。
次に:
- (∀a∈A. a ≦ g(f(a))) ∧ (∀b∈B. f(g(b)) ≦ b)
このとき、fとgは随伴ペアです。詳しくは次の記事を参照してください。
逆ペアと随伴ペアの中間の存在として:
- (∀a∈A. a = g(f(a))) ∧ (∀b∈B. f(g(b)) ≦ b)
このとき、fとgはEPペア〈EP pair〉と呼びます。EPは"embedding-projection"のことで、fが単射埋め込み、gがそれに対する全射射影と解釈できます。∀a∈A. a = g(f(a)) だけなら、gをレトラクション〈引き込み〉と呼ぶので、ER〈embedding-retraction〉ペアです。(もっとも、EPペアとERペアは明確に区別されないようです。)詳しくは次の記事を参照してください。
変数水増しと空虚な束縛
集合(議論の領域)Y上の述語全体の集合をPred[Y]と書きます。'Pred'と太字にしたほうが圏論と相性がいいですが、面倒なんで太字にしません。Pred[X×Y]も同じ解釈です。
π2:X×Y→Y は第二射影とします。この第二射影により、述語(真偽値をとる関数)の引き戻し π2*:Pred[Y]→Pred[X×Y] が誘導されます。
- π2*(Q) := π2;Q = Q
π2
すぐ上の定義は、意味的に考えたものですが、構文的にπ2*を考えると、変数yだけを含む(可能性がある)論理式Qを、ニ変数x, yの論理式だと“思い直す”ことです。“思い直す”だけなので、実際には何も起きず、分かりにくい操作です。
例えば、Q ≡ (y2 = 2) として、π2*(Q) は、見た目はQとまったく変わりません。見て区別できません。しかし、変数xとyを持つ論理式とみなした y2 = 2 なので、π2*(Q) = P なのです。ここで、Pは前節で定義した「たまたまxを含まない二変数論理式」です。
P, Qを意味的に考えて、真偽値をとる関数と解釈するなら:
- Q = λy∈R.(y2 = 2)
- P = λ(x, y)∈R.(y2 = 2)
実際には出現しない変数を足していくことを変数水増し〈variable thinning〉と呼びます。定数を関数とみなすのも変数水増しです。
- C0 = 3 (ほんとの定数)
- C1 = λx∈R.3 (一変数の定数関数)
- C2 = λ(x, y)∈R×R.3 (ニ変数の定数関数)
空虚な束縛や変数水増しは、構文的な操作ですが、構文的に考えていると分かりにくく正体不明です。意味的に考えましょう。集合X上の命題Pは、P:X→{True, False} という真偽値関数とみなせば意味的解釈になりますが、さらに、外延的に考えて {x∈X | P(x)} のような集合を命題の意味としましょう。
すると、π2:X×Y→Y に伴って、逆像関数 π2*:Pow(Y)→Pow(X×Y) が定義できます。ここで、Pow(-) はベキ集合を表します。
- π2*(B) := {(x, y)∈X×Y | π2(x, y)∈B} = {(x, y)∈X×Y | y∈B}
存在記号∃に対応する写像は π2*:Pow(X×Y)→Pow(Y) で、次のように定義される像関数 π2*:Pow(X×Y)→Pow(Y) です。
- π2*(A) := {y∈Y | ∃x∈X.(π2(x, y) = y ∧ (x, y)∈A)} = {y∈Y | ∃x∈X.((x, y)∈A)}
この状況ならば、π2*, π2* の随伴性が見えやすくなります。次の図は「存在記号の除去規則について考える」で出したもので、設定が少し違います(第二射影じゃなくて第一射影)が、ヒントになるでしょう。
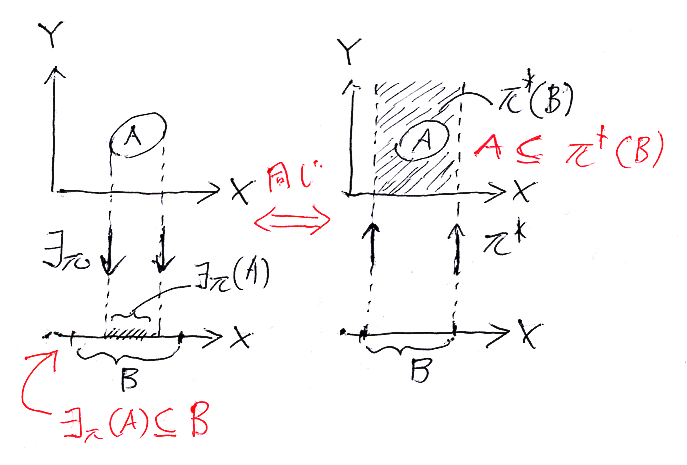
射影の逆像と像はEPペア
ここから先は、X×Y→Y という射影を単にπと書くことにします。毎回下付き'2'を書くのはめんどくさいし、第一射影でも第二射影でも話は変わらないので。
前節で述べた逆像写像は、π*:Pow(Y)→Pow(X×Y) です。逆像写像を引き戻し〈pullback〉とも呼びますが、πと逆方向に部分集合を移すからです。述語(真偽値関数)Pに対するπの前結合 Pπ も、部分集合Bの逆像 {(x, y)∈X×Y | π(x, y)∈B} も、どちらも引き戻しと呼び、π*(-) で表します。圏論のファイバー積も引き戻しなので、「引き戻し」は多義語です。
A∈Pow(X×Y) に対する像 π*(A) は、
- π*(A) = {y∈Y | (x, y)∈A である x∈X が存在する}
像を対応させるπ*、その値 π*(A) を前送り〈pushuout | push-forward〉とも呼びます。
π*とπ*のあいだに次の関係があるのはすぐに分かるでしょう。
- B∈Pow(Y) に対して、π*(π*(B)) = B
- A∈Pow(X×Y) に対して、A ⊆ π*(π*(A))
これは、π*とπ*がEPペアになっていることです。π*がembeddingで、π*がprojectionです。
π*の論理的構文的解釈が存在限量子∃なので、π*と∃がEPペアと言っても同じです。さらに、π*の論理的構文的解釈が変数水増しオペレータなので、変数水増しオペレータと存在限量子がEPペアとも言えます。EPペアは、随伴ペアの特殊なものだったので、変数水増しオペレータと存在限量子は実際に随伴ペアです。
上記の事実を、論理的構文的にいえば:
- ∃x∈X.Q(y) ⇔ Q(y)
- P(x, y) ⇒ ∃x∈X.P(x, y)
変数水増しオペレータは表面に現れないので、[x, y]という形で無理に表現すれば:
- (∃x∈X.[x, y]Q(y)) ⇔ Q(y)
- P(x, y) ⇒ [x, y](∃x∈X.P(x, y))
全称限量子の場合は、少し複雑になりますが、同じスジミチをたどって、次が得られます。
- P(x, y) ⇔ ([x, y]∀x∈X.P(x, y))
- ([x, y]∀x∈X.P(x, y)) ⇒ P(x, y)
ここまで話した内容は、射影、像、逆像、補集合などの意味的(集合論的)な事実を、EPペアや随伴性を介して論理的構文的に再解釈してみたのです。論理では構文論(論理式と証明)のウェイトが高いですが、構文論だけではなかなか理解しにくいこともあるので、意味的解釈を併用しましょう -- というハナシでした。