最初に言っておくと、これはマジな話です。ジョーダンやネタじゃないです。絵やテキストにおける、上下左右のひっくり返し/裏返しに慣れないと、双対や随伴の理解は困難です。いやっ、ホントに。
絵図とテキストにおける向き
圏論的な絵算(pictorial/graphical/diagrammatic calculation)で使うストリング図を描くときの方向の取り方が人によりバラバラだという話を何度かしています。
射や自然変換の方向(第一の方向)とモノイド積や関手の方向(第二の方向)を、それぞれ上下左右のどの向きにとるか? ということが問題なんです。第一方向、第二方向の順で矢印を使って表すと、選択肢は全部で8種類あります。
- ↓→
- ↓←
- ↑→
- ↑←
- →↓
- ←↓
- →↑
- ←↑
僕は主に最初の方式で、射は上から下、関手は左から右に描きます。多数派・少数派の別はありますが、すべての方式が使われています。
図をテキストに写し取るときも、図の方向をテキスト上ではどっち向きに取るかにより図式順記法(diagrammatic order notation)と反図式順記法(anti-diagrammatic order notation)があります。
現状、僕が使っている標準的な記法(世の中の標準じゃない!)は次のとおり。
| 図の向き | 図式順演算子記号 | 反図式順演算子記号 | 例 | |
|---|---|---|---|---|
| 第一方向 | ↓ | ; | |
射 f;g |
| 第ニ方向 | → | *, |
・, ● (ドット) | 関手 F*G |
自分で図示・計算するときはもっぱら図式順を使いますが、世間の多数派は反図式順なので、書き換えるときが多いです。図式順と反図式順(例:';'と'・')が混じった式を使わざるを得ないこともあります。どれかひとつの方式に統一なんて不可能です。
平面における向きの変換
ストリング図を描く平面に、普通のx-y座標が入っているとします。先に挙げた8種類のバリエーションは、x軸対称変換、y軸対称変換、x軸とy軸の入れ替え変換を組み合わせて作った変換に対応します。平面の変換を行列で表すなら:
平面内に描かれた絵(ストリング図)を、これらの変換で写すと、別な方式の絵になります。自分が使う方式を決めておいても、皆んながそれを使っているわけではないし、双対や随伴では絵をひっくり返す/裏返すことになります。
ひとつの絵が、上記の8つの変換でどう変わるかを知ってないと、ストリング図を読み書きするのは難しいです。この困難や負担は、実にバカにできないもので、僕はだいぶ疲弊消耗しました。
文字の変換
いま、あるテキスト(文字の並び)が左から右の横書きで書かれていたとしましょう。これに、y軸対称変換をほどこすとどうなるでしょうか。"hello"が"olleh"になる? いえ、テキストも図形とみなすなら個々の文字も左右がひっくり返ります。つまり、鏡文字フォントで右から左に文字を並べた図形になります。
 [*1]
[*1]
上の鏡文字フォントの画像は、「圏論的ひっくり返し:単純なケース」で説明に使ったものです。圏の双対(反対; opposite)の話でした。
「コンパクト閉圏と絵算で理解する線形代数とシーケント計算(入り口だけ)」でも、文字自体を180度回転して双対を表現しました。
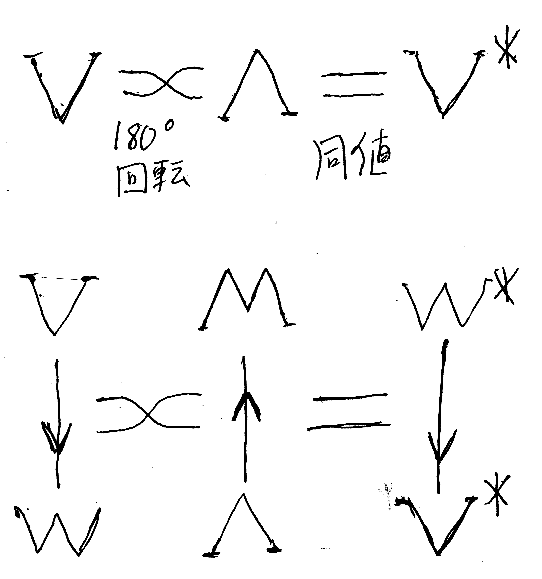
テキストについても、文字の並び順と個々の文字の形状の変換に慣れておいたほうがいいと思います。「そんな必要あるの?」と訝〈いぶか〉しく感じるでしょうが、どんな方向にも文字列や数式を書けるのは確かに有利なんです。(そのうち、実例を出すつもりです。)([追記]「記法バイアスと記法独立な把握: 順序随伴を例として」に実例を書きました。[/追記][追記]「存在記号の除去規則について考える」でも縦横の入れ替えを何度かしています。[/追記])
文字もひっくり返したほうが自然である状況証拠として、セリンガーのテキスト"A survey of graphical languages for monoidal categories"(https://arxiv.org/abs/0908.3347)から絵を引用します。
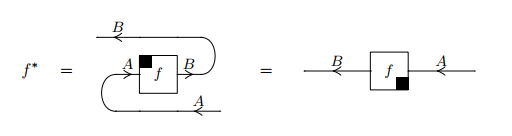
ひっくり返しフォントは使ってませんが、射fがひっくり返っているのを明示するため、ボックスの隅に黒い印を描いています。fは上下も左右もひっくり返っているのです。
文字'x'や'A'は変換しても形があまり変わらないので、'a', 'L', '≦', ';'などの文字のひっくり返し/裏返し、それが出来たら短い文字列のひっくり返し/裏返しを練習するといいでしょう。
コーヒーでも飲みながら
僕は飲食店の紙ナプキンで、絵と文字の変換の練習をします。文字'h'とアローヘッドが半分の矢印を、8種の方向で描いてみます。アローヘッドが半分の矢印とは、ハープーン(もり)と呼ばれる記号で:
ハープーンに'h'を乗せて、8種の方向で描くとこんな感じ↓

双対性/随伴性を表すニョロニョロの左右ひっくり返しなら:
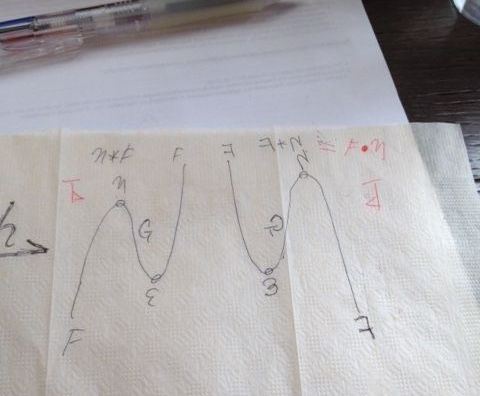
紙ナプキンは、向きを変えたり裏返しがすぐに出来るし、薄くて透けているので、正しく鏡映が描けているかの確認も楽です。
コーヒーを飲み終わって、紙ナプキンを数枚消費したら帰ります。
