3-圏と、3-圏からモノイド圏への関手 -- toward 量子と古典の物理と幾何＠名古屋

「ストリンググラフのレベル関数と全順序 -- toward 量子と古典の物理と幾何＠名古屋」にて：

ストーリーを組み立てるためのピースはあと2つ；とある代数系の話と高次関手の構成法です。

「高次関手の構成法」を話題にします。一般に高次圏のあいだの高次関手の記述や構成は難しい問題ですが、色々な条件を付けて特別に単純なケースを考えることにします。

内容：

悩みのタネ：文字・記号が足りない！
3-圏の記述
断片構造
3-圏としてのモノイド圏の記述
3-圏からモノイド圏への関手：状況
3-圏からモノイド圏への関手：定義

悩みのタネ：文字・記号が足りない！

高次圏の難しさ（のひとつ）は、最初の一歩を踏み出すのに労力が矢鱈かかることでしょう。高次圏を定義する／記述する／構成することは大変です。扱うモノを定義して例を出す、という最初のところで疲れます。定義や例の構成が難しいので、それが目的となることもしばしばあります。

射（セル）の種類がたくさんあるので、文字や記号がすぐに不足します。かといって、オーバーロード（文字・記号の多義的使用）は、やり過ぎると誤解や混乱のもとになります。できるだけ整合的でスッキリした記号法にしようと思っても、従来からの伝統や常識があるので、あまり新奇な記号法は使えません。伝統・常識的な記法は、律儀に守ろうとすると不整合や不具合で破綻したりします。

もう、どうすりゃいいの!? という気分ですが、トライ・アンド・エラーで試しては改善していくしかないのでしょう。この記事で使っている記法もトライアル的なものです。

3-圏の記述

AKB12（「従順な複体から作られる3次元の圏」参照）のような3-圏を考えます。ただし、AKB12そのものでなくてもいいので、主題とする3-圏をKと書きます。Kは固有名詞ではなく、次の性質を持つ3-圏一般を指します。主たる事例は、もちろんAKB12です。

h（横／水平）、v（縦／垂直）、t（横断的）の3つの方向を持つ。
射の種類は、0, h1, hv2, t1, ht2, 3で識別される6種類である。
P, Q∈|K|₀ に対して、PからQへのt1-射は高々ひとつしかない。

3番目の仮定から、t1-射は極端に単純なので、特別に扱います。PからQへのt1-射が存在するならば、それは1つしかないので、(P>Q)と書くことにします。

話を簡単にするために、h, v, tのすべての方向で結合演算（3種類ある）は“厳密に結合的かつ単位的”（strictly associative, strictly unital）であるとします。つまり、厳密3-圏を考えます。AKB12では、h-方向、v-方向の結合をコファイバー和（貼り合わせ）で定義しているので、演算法則は厳密ではありません。しかし、厳密（on-the-nose）だと思っても実際上の問題は起きないので、厳密性の仮定は許容できるでしょう。

6種類の射（セル）は、次のような表記で区別することにします。「グレード」は射の種類のことです（「高次圏の次元について」を参照してください）。

グレード	表記	備考
0	P, Q	アルファベットの後のほうの大文字
h1	a, b	アルファベットの最初のほうの小文字
hv2	A, B	アルファベットの最初のほうの大文字
t1	(無名)	名前を付けずに(P>Q)と書く
ht2	f, g	アルファベットの中ほどの小文字
3	α, β	ギリシャ小文字

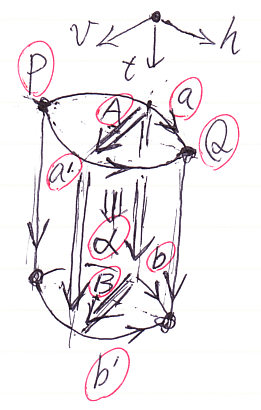
各種の「dom/cod, ;, id」は次のような記号を使うことにします。

グレード	h-方向	v-方向	t-方向
h1	left/right, *, unit
hv2	left/right, *, Unit	top/bottom, #, triv
t1			dom/cod, id, ;
ht2	left/right, *, unit		dom/cod, id, ;
3	left/right, *, Unit	top/bottom, #, triv	dom/cod, id, ;

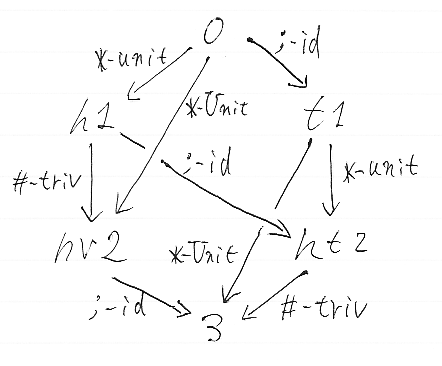
id写像（低い次元の射を恒等／単位として高い次元の射とみなす写像）だけを図示すると次のようになります。id写像の値は、二項演算'*', '#', ';'に対する恒等／単位となります。大文字で始まるUnitは次元を2あげるものです。

次のような表現が意味を持つことになります。

0-射： P, Q, left[a], right[a], left[A], right[A], dom[(P>Q)], cod[(P>Q)]
h1-射： a, b, a*b, unit[P], top[A], bottom[A], dom[f], cod[f]
hv2-射： A, B, A*B, A#B, Unit[P], triv[a], dom[α], cod[α]
t1-射： (P>Q), (P>Q);(Q>R), id[P], left(f), right(f), left(α), right(α)
ht2-射： f, g, f*g, f;g, unit[(P>Q)], id[a], top[α], bottom[α]
3-射： α, β, α*β, α#β, α;β, id[A], Unit[(P>Q)], triv[f]

これらの表現は、次の図を見ながら書き出しました。先のid写像の図と基本的に同じですが、二重線の部分に「dom/cod, id」構造があります。二重線に付記している記号は、そこの「dom/cod, id」構造に載る二項演算です。

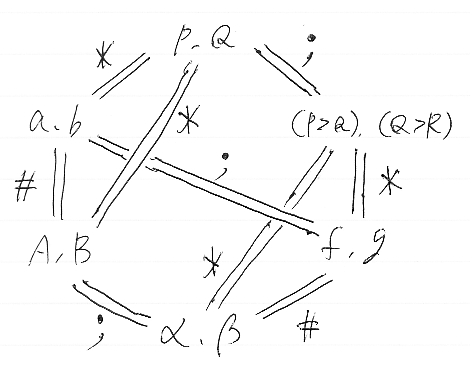
この図から、3-圏のなかに1-圏構造、2-圏構造が入れ子になって織り込まれていることが分かります。

断片構造

前節の最後で言ったように、1つの3-圏の内部に1-圏（通常の圏）がいくつも織り込まれています。高次圏のなかに埋め込まれて存在する通常の圏を断片圏（fragment category）と呼ぶことにします。断片圏は、もとの高次圏より扱いやすいので、高次圏を調べる道具になります。ときには、断片圏の情報で十分なこともあります。

断片圏を表すために、射と対象となる構成素の種類（グレード）と結合の方向で示すことにします。具体例を出します。

K^1-cat_{0, h1 / h} = (|K|₀, |K|_h1, left, right, unit, *)
K^1-cat_{0, t1 / t} = (|K|₀, |K|_t1, dom, cod, id, ;)
K^1-cat_{hv2, 3 / t} = (|K|_hv2, |K|₃, dom, cod, id, ;)

同様にして、断片2-圏（fragment 2-category）を取り出すこともできます。今回の例で注目すべき断片2-圏は次の2-圏です。

K^2-cat_{0, h1, hv2 / h, v} = (|K|₀, |K|_h1, |K|_hv2, left, righ, unit, *, top, bottom, triv, #)

断片構造として二重圏（double category）も存在します。次が断片二重圏（fragment double category）の例です。

K^d-cat_{0, h1, t1, ht2 / h, t} = (|K|₀, |K|_h1, |K|_t1, |K|_ht2, left, righ, unit, *, dom, cod, id, ;)

これらの断片構造とホム構造（ホム集合、ホム圏、ホム2-圏など）を組み合わせると、さらに多彩な構造を高次圏から抽出できそうですが、そのための計算法を整備する必要があります。

3-圏としてのモノイド圏の記述

Kを今まで述べたような3-圏として、Kからモノイド圏Cへの関手を考えたいのです。このためには、モノイド圏を3-圏とみなして、3-関手を考えることになります。しかし、モノイド圏は安定した定義と定着した記法を持つので、これらの定義・記法を変更したくありません。

そこで、折衷案として、モノイド圏概念は変更せず、モノイド圏Cに付加的構造を追加することにします。C = (C, $\otimes$ , I, α, λ, ρ) をモノイド圏とします。α, λ, ρは律子ですが、省略することもあります。台圏（underlying category）としてのCは、通常通り「dom, cod, id, ;」で定義されているとします。

₀ =

= Obj(C),

₁ = Mor(C) という記法を使います。他に、集合

_-1,

₂ を定義します。

|C|_-1 = {0}
|C|₂ = {Id[f] | f∈Mor(C) }

_-1は単元集合で、その要素は何でもいいです。

₂は、

₁と同型な集合で、その同型写像は Id:

₁→

₂ で与えられます。他に、left, right, unit, dom, cod, IdId, Dom, Codを次のように定義します。

left:|C|₀→|C|_-1 left[X]= 0
right:|C|₀→|C|_-1 right[X] = 0
unit:|C|_-1→|C|₀ unit[0] = I
dom:|C|₂→|C|₀ dom[Id[f]] = dom[f]
cod:|C|₂→|C|₀ cod[Id[f]] = cod[f]
IdId:|C|₀→|C|₂ IdId[X] = Id[id[X]]
left:|C|₂→|C|_-1 left[Id[f]] = 0
right:|C|₂→|C|_-1 right[Id[f]] = 0
Dom:|C|₂→|C|₁ Dom[Id[f]] = f
Cod:|C|₂|C|₁ Cod[Id[f]] = f

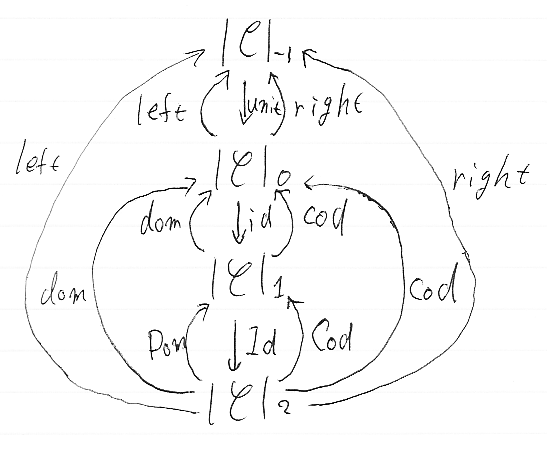
これで、グレードの値の集合が{-1, 0, 1, 2}であるような3-圏とみなせます。|C|₂は3次元の射の集合ですが、グレードは2です。グレード／次元は「モノの見方」で変わるので、このあたりのズレは致し方ないです。

₂上には3つの二項演算 $\otimes$ , ;, ;; が存在します。2-射（

₂の要素）をξ, ηなどで示します。

方向	演算	定義可能条件	定義
横	$\otimes$	right[ξ] = left[η]	Id[f] $\otimes$ Id[g] := Id[f $\otimes$ g]
縦	;	cod[ξ] = dom[η]	Id[f];Id[g] := Id[f;g]
横断的	;;	Cod[ξ] = Dom[η]	Id[f];;Id[f] := Id[f]

上記の表で、条件「right[ξ] = left[η]」は常に成立します。条件「Cod[ξ] = Dom[η]」は ξ = η = Id[f] を意味します。横断的方向への結合演算;;は自明な演算です。

もともとあった|C|₀, |C|₁に対してダミー対象の単元集合|C|_-1と、恒等2-射の集合|C|₂を付け加え、自明な3-圏（次元はズレている）の構造を定義しました。

以上で、モノイド圏Cを3-圏とみなすことができました。ただし、形の上で3-圏にしただけで、新しい構造・情報は何もありません。名ばかり／形ばかりの3-圏です。

3-圏からモノイド圏への関手：状況

Kを先に記述した3-圏とします。Cをモノイド圏として、必要があれば前節の方法で3-圏とみなします。KからCへの関手を構成したいのですが、そもそも関手とはなんであって、どう定義するかを決めなくてはなりません。

A, Bが通常の圏として、そのあいだの関手は2つの写像 F₀:|A|₀→|B|₀とF₁:|A|₁→|B|₁により定義されます。F₀, F₁が、dom, cod, id, ; と協調（整合）するという条件が付きます。高次圏でも同様に、射の種別（グレード）ごとに写像を設定し、それらの写像達が圏の構造と協調するという条件を付ければいいでしょう。3-圏Kとモノイド圏Cの場合に、具体的に見ていきましょう。

関手Fを構成する写像は次のとおりとします。

F₀:|K|₀→|C|_-1
F_h1:|K|_h1→|C|₀
F_hv2:|K|_hv2→|C|₁
F_t1:|K|_t1→|C|₀
F_ht2:|K|_ht2→|C|₁
F₃:|K|₃→|C|₂

3-圏Kを構成する射の種類（グレード）ごとに場合分けして、6個の写像を使用します。関手の行き先であるモノイド圏Cは、あまり自由度がないので、Cへの関手は強い制限を受けます。この制限のために、6個の写像のうちの幾つかは自明になります。

|C|_-1 = {0} なので、F₀の値は0に固定される。F₀について考える必要はない。
|C|₂ の要素は恒等2-射なので、F₃(α) は、F_hv2(dom[α]) の値だけで決まる。F₃の存在は、F_hv2の性質として記述できる（後述）。
F₃(α)の値が恒等2-射なので、F_ht2(top(α))の値は恒等1-射となる。
F_t1の値はモノイド単位Iに固定される。F_t1について考える必要はない。

以上の事情から、F₀とF_t1について考える必要はなく、F₃とF_ht2は、F_hv2から自動的に決まります。よって、関手として定義すべき写像は F_h1:|K|_h1→|C|₀ と F_hv2:|K|_hv2→|C|₁ の2つだけになります。

この状況を大ざっぱに図示すると次のようになります。シリンダー状のKの3-射が、Cの射のあいだの恒等（等式）に写されます。

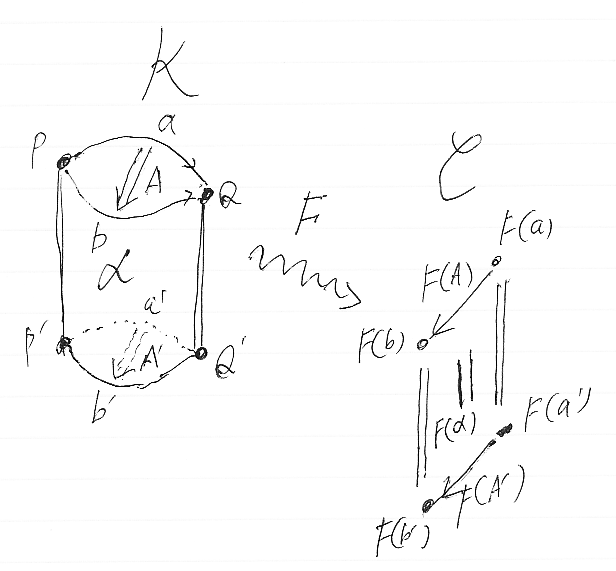
3-圏からモノイド圏への関手：定義

前節で述べた状況を踏まえて、関手 F:K→C を改めて定義しましょう。

関手Fを構成するのは2つの写像です。（F_h1をF₁、F_hv2をF₂と略記した。）

F₁:|K|_h1→|C|₀
F₂:|K|_hv2→|C|₁

F₁, F₂は次を満たします。

a, b∈|K|_h1 が横結合可能なら、F₁(a*b) $\stackrel{\sim}{=}$ F₁(a) $\otimes$ F₁(b)
任意のP∈|K|₀ に対して、F₁(unit[P]) $\stackrel{\sim}{=}$ I
A, B∈|K|_hv2 が横結合可能なら、F₂(A*B) $\stackrel{\sim}{=}$ F₂(A) $\otimes$ F₂(B)
任意のP∈|K|₀ に対して、F₂(Unit[P]) $\stackrel{\sim}{=}$ id[I]
A∈|K|_hv2 に対して、F(top[A]) = dom[F(A)], F(bottom[A]) = cod[F(A)]
A, B∈|K|_hv2 が縦結合可能なら、F₂(A#B) $\stackrel{\sim}{=}$ F₂(A);F₂(B)
任意の a∈|K|_h1 に対して、F₂(triv[a]) = id[F₁(a)]

さらに、Kの3-射に対してCの恒等2-射を割当て可能とするために、次の条件も課します。

任意の α∈|K|₃ に対して、dom[α] = A, cod[α] = B ならば、F₂(A) = F₂(B)

この条件に別な解釈を与えておきましょう。Kの3-射 α:::A≡>B は、2-射AとBのあいだの同値を与えるものだと解釈します。その同値関係を'〜'とすると：

A〜B ⇔ α:::A≡>B または β:::B≡>A という3-射が存在する

これだけだと、'〜'が推移律を満たすことが保証できないので、推移的閉包を取ります。別な言い方をすると、Kの3-射はすべて可逆であると考えた場合の同型関係が'〜'です。'〜'をチャンと構成するのはけっこう面倒ですが、これ以上は踏み込まないことにします。

同値関係'〜'を使って先の条件を書き換えると：

任意の A, B∈|K|_hv2 に対して、A〜B ならば、F₂(A) = F₂(B)

Fは、Kの2-射のあいだの同値性をCの等式に写すことになります。関手Fが満たすべき性質を同値性の観点からもう一度述べてみると：

Fは、Kの1-射の横結合を、Cの対象のモノイド積に写す。
Fは、Kの2-射の横結合を、Cの射のモノイド積に写す。
Fは、Kの2-射の縦結合を、Cの射の結合に写す。
Fは、Kの3-射による2-射間の同値関係を、Cの射の等式（等値関係）に写す。

もっと手短に言うと：

Fは、Kの横結合を、Cのモノイド積に写す。
Fは、Kの縦結合を、Cの結合に写す。
Fは、Kの同値関係を、Cの等式に写す。