証明支援系Globularを使っている人っているのかな? まー、いても少数でしょうね。僕はたまに使います。しばらく使わないでいると使い方を忘れます。少なくとも一人のユーザー(=僕・檜山)にとっては意味があるので、「Globularの使い方」を記録しておきます。
何回かに分けますが、気が向いたら書くつもりなので全体で何回になるか分かりません。何をどこまで書くかの計画もありません。
内容:
シリーズ目次
はじめに
Globularは、機能的には“ある種の”お絵描きソフトです。普通のお絵描きソフトと違うのは、n次元(n = 0, 1, 2, 3, 4, 5, ...)のキャンバスに絵(?)を描けることです。「Globularの威力をお見せしよう」で紹介した僕のサンプル(http://globular.science/1601.004v2)は、4次元の絵を使っています。「モノイド圏の単位対象の定義について: これ難しいやん」で触れたヴィカリー(Jamie Vicary)による「λI = ρI」の証明(http://globular.science/1512.002v1)は5次元の絵です。
もちろん、Globularは画家やイラストレーターが使うものではありません*1。描いた絵(n次元の図形)は証明になるので、証明を書くためのツール=証明支援系として使います。絵を描くことが何故に証明になるのか? 次の記事で説明を試みています。が、これはなかなか分かりにくい話題です。
Globularは未来のコミュニケーションのためのツールです(「「コミュニケーションの多次元化」という革命に立ち会っているのだと思う」参照)。現時点では、実験的なソフトウェア(proof-of-concept software)であり、機能性や使い勝手はマダマダです。要望や不平を言い出すとキリがないです。3次元ビュー、まともなアニメーション機能、5次元以上の正しい計算モデルなどは(ユーザーなら)誰でも欲しいでしょうが、実現するのは何年先でしょうか? このソフトウェアの性格からいって、10年、20年のスパンで進化と成長を見守るべきでしょう。
参考URL
- ソフトウェア: http://globular.science/ (chromeブラウザ推奨)
- ヘルプページ: https://ncatlab.org/nlab/show/Globular
GlobularのソースコードはGithubでホストされています。ライセンスはWTFPL (Do What the Fuck You Want To Public License) *3です。
Globularをテキスト(文字で書かれた文章)で説明するのは難しい*4ので、ビデオチュートリアルがあります(15分ちょい)。
僕は英語を聴き取ることが出来ないので次のようにしています。
- 「字幕」をONにする。英語字幕が出て、目で読めるようになります。
- 再生速度を「0.75」にしておくと、字幕を読むのが楽です。
- 必要に応じて停止や巻き戻しを使います。
Globularに関する論文:
- Title: Globular: an online proof assistant for higher-dimensional rewriting
- Authors: Krzysztof Bar, Aleks Kissinger, Jamie Vicary
- Pages: 18p
- URL: https://arxiv.org/abs/1612.01093
理論寄りですがマニュアルとして使えます。短いので、説明はちょっと雑です。
- Title: Data structures for quasistrict higher categories
- Authors: Krzysztof Bar, Jamie Vicary
- Pages: 112p
- URL: https://arxiv.org/abs/1610.06908
Globularで使われているデータ構造とアルゴリズムが詳しく解説されています。この論文の内容を口頭発表したときの動画(50分弱)があります。
このなかにも、デモとチュートリアル(9:40--32:50の13分くらい)が含まれています。
Globular登場以前の2012年に書かれたモノですが、次の論文に、1, 2, 3次元のストリング図(ドット図、狭義のストリング図、サーフェイス図)の丁寧な説明があります。とても参考になります。
- Title: Surface diagrams for gray-categories
- Authors: Benjamin Taylor Hummon
- Pages: 142p
- URL: http://escholarship.org/uc/item/5b24s9cc
ワークスペースの管理など
Globularによる成果物や作業の状態は、ワークスペース(workspace)と呼ばれます。ワークスペースは、一個のJSONファイルとして保存や転送ができます。JSONとは言っても、次のような感じなんで事実上バイナリですけどね。
{"compressed":"8xx7Il90IjoiUHJvamVjdCIsImRpYWdyYW0iOm51bGwsInNpZ25hdHVyZSI6KwAVUxIAsSwiY2VsbHMiOnt9KQAkbWE2APQPayI6MCwibiI6MH0sImNhY2hlU291cmNlVGFyZ2V0JgDxD2luaXRpYWxpemVkIjp0cnVlLCJ2aWV3X2NvbnRyb1kAIyJwmQAAUADDc2xpY2VzIjpbXX19jQAPuACSwHNsaWNlcyI6W119fQ==","original_length":184}
Save, Export, Importの3つのコマンドでワークスペースを管理できます。Saveコマンドはサーバー側のストレージへのワークスペースの保存なので、アカウントが必要です。アカウントは[SIGN UP]メニューから作れます。アカウントで[LOG IN]すると、[WORKSPACES]メニューが出現し、サーバー側に保存しているワークスペース達の管理やロードができます。サーバーに置いたワークスペースはパブリックに公開したり、知人と共有できます。公開されているワークスペースは[GALLERY]で閲覧できます。なお、アカウントがなくても、ワークスペースのローカルディスクへの保存と読み込み(ExportとImport)はできます。
画面上に見えているダイアグラム(描いた図形)のビューを画像ファイルにするにはGraphicコマンドを使います。ビューのスナップショットが、PNGファイルとしてローカルに保存されます(画像ダウンロードと同じ挙動)。
[HELP]でnLabのGlobularヘルプページを(別タブで)表示します。
以上で、[LOG IN]/[SIGN UP]/[LOG OUT], [WORKSPACES], [GALLERY]メニュー項目、Save, Export, Import, Graphicコマンドの説明は終わりです。これから先は、n次元の図形(それが証明になる)を描くコマンド/マウス操作の解説に集中します。
画面構成
画面上部のメニューと画面右側のコマンドボタンを除くと、画面は2つの部分に分けられます。
左側がセルパレット

Globularの理論的な用語では、指標(signature)と呼びます。ソフトウェアのUIコンポネントとしてはセルパレット(cell palette)と呼ぶことにします。
セルパレットのなかは、0-Cells, 1-Cells, 2-Cells, ... のように次元ごとに区分けされていて、各次元のダイアグラムのサムネイルが表示されています。パレット(指標)の要素となっているダイアグラムをセル(cell)と呼びます。
Globularで行う作業は、セルパレット(指標)を構築することで、主たるワークスペース・データはセルパレットをバイナリエンコード(シリアライズ)したものです。
中央がビューペイン
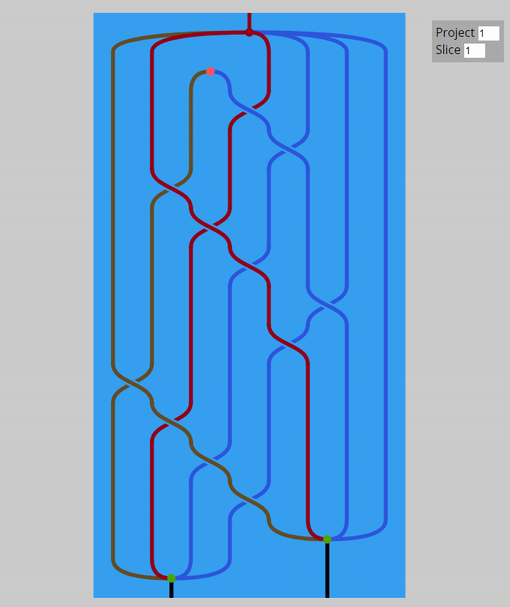
ビューペインに、現在作業中のダイアグラムのビュー(view)が表示されます。「ビューペイン」と「ビュー」は区別してください。ビューペインは、画面(ブラウザウィンドウ)の一部を占めるUIコンポネントで、2次元矩形領域です。それに対して、ダイアグラムのビューとは、ダイアグラムを可視化(visualize)したグラフィック・オブジェクトで、次元は2次元、1次元、0次元の3種があります。
上の画面ショットは2次元ビューです。次に挙げる画面ショットは、1次元のビューです。グラフィックスとしては、点が大きさを持ち/線が太さを持つように描きますが、概念的には点と線からなる1次元図形です。
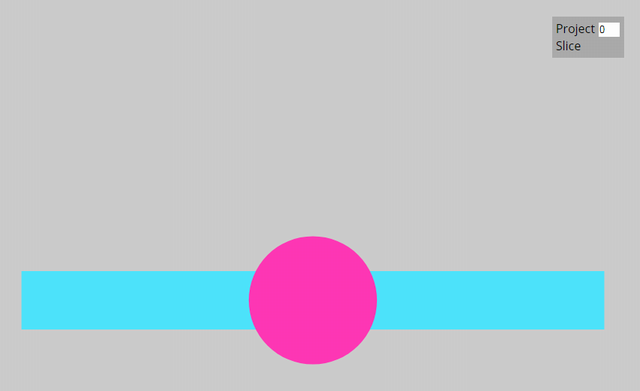
点だけからなるビューが0次元ビューです。点もけっこう大きな色付き円板で描きますが、次元は0です。ビューペインのなかでビュー(グラフィック・オブジェクト)が描かれてない余った領域はグレー背景色となります。
ビューコントロールとビューイング方式
ビューペインの右上にあるコントロールをビューコントロール(view control)と呼びましょう。次のようなモノです。
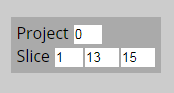
ビューコントロールは、整数値のアップダウン・コントロール(numeric up-down cotrol)を複数組み合わせた複合コントロールです。上部がProjectコントロール、下部がSliceコントロールです。Projectコントロール(up-down)は常に表示されてますが、Sliceコントロールは必要に応じて増減します。
最初に出した2次元ビューでは、1個のSliceコントロール、二番目の画面ショットである1次元ビューでは0個のSliceコントロール、すぐ上の画面ショットでは3個のSliceコントロールが出ています。
ビューコントロールの意味と使い方を理解するには、Globularがサポートしているビューイング方式(viewing method)を知る必要があります。ヘルプ/マニュアルで言及されてないのですが、スチル方式(still picture method)とスライシング方式(slicing animation method)と呼ぶことにします。一枚の静止画として見るのがスチル方式、何枚かの画像を紙芝居(パラパラ漫画)としてめくりながら見るのがスライシング方式です。
スチルで見るか、スライシングで見るかをユーザーは選べません。Globularが自動で方式を選択してしまい、変更不可能です。可視化すべき対象の図形の次元が2以下なら常にスチル方式です。図形の次元が3以上だと、ビューの次元を2次元まで落とすようにスライシングが選ばれます。
上記の「可視化すべき対象の図形」が“作業中のダイアグラムそのもの”かというと、そうではありません。可視化に先立って、n次元ダイアグラムは射影(project)されます。例えば、4次元ダイアグラムを3次元空間に射影して3次元ダイアグラムを作ります。射影像である3次元ダイアグラムがビューイングの対象になります。
射影の次元は、Projectコントロールにより自由に指定できます。4次元ダイアグラムを3次元空間に射影するときは、次元の差である1をProjectコントロールに指定します。3ではないので注意しましょう。射影の概念的実体は、(x, y, z, w)|→(x, y, z)のような単純な線形写像です*5。Projectコントロールに指定する整数は、線形代数のナリティ(nullity, 核空間の次元: nullity(f) = dim(ker(f)))です。
n次元ダイアグラムをナリティk(k = 0 でもよい)を指定して射影すると、(n - k)次元の射映像ができます。
- n - k ≦ 2 ならスチル方式でビューイングする。
- n - k > 3 ならスライシング方式でビューイングする。このとき、(n - k - 2)個のSliceコントロールが出現する。
例えば、5次元ダイアグラムをナリティ1で射影すると、5 - 1 = 4次元の射影像ダイアグラムができて、4 > 2 なので、4 - 2 = 2個のSliceコントロールが出現します。ナリティ0(事前に何もしない)のときは、3個のSliceコントロールが出ます。
これで、画面構成と各UIコンポネントの説明は終わりです。しかし、ダイアグラムの射影やスライシングが実際のところ何をすることなのかを知らないと、使い方わかりませんよね。そもそも、ビューイングするおおもとの幾何的対象物であるダイアグラムが何であるかを理解しないとね。
それは次回以降に(次回以降があれば)。
