統計的独立性と線形独立性を共通に語ることは出来るのか？

統計的独立性は確率・統計において重要な概念です。「独立」という言葉は色々な分野で使われます。おそらく一番お馴染みな独立性は、統計的独立性ではなくて線形独立性でしょう。単語として「独立」が使われているからといって、統計的独立性と線形独立性が関係するとは考えにくいですよね。

しかし、とある枠組み〈フレームワーク〉のなかでは、二者を統一的に説明することが可能です。

内容：

統計的独立性

確率的な試行をn回するとします。例えば、サイコロを3回ふる（試行＝サイコロふり、n = 3）とかです。i回目（1 ≦ i ≦ n）の試行を、確率変数X_iで表現するとして、X₁, X₂, ..., X_n は、通常は独立だと仮定されます。

幾つかの確率変数が独立であることをチャンと定義するのは、けっこう難しい話になります。が、今は何らかの方法で独立性が定義できたとしましょう。「独立」という言葉は様々な分野で様々な意味で使われるので、サイコロふりなどで現れる独立性は、確率変数の確率的／統計的独立性と呼ぶことにします。ちょっと長すぎるので、次のように省略するのは許します（不用意に「独立性」とは言わない）。

1. 確率変数の独立性〈independence of random variables〉
2. 確率的独立性〈stochastic independence〉
3. 統計的独立性〈statistical independence〉

統計的独立性を定義するために使われる諸々の概念・用語； 「確率変数」、「確率分布」、「母集団」などはだいぶ曖昧で混乱しています。その点については、次の記事とそこから参照されている他の記事を見てください。

• 「確率変数」の正体は米田埋め込み
• 確率・統計の「分布」の意味と使用法
• 超曖昧語「母集団」「標本」にケリをつける

フランツの定義とシンプソンの定義

統計的独立性（の一般化）を、圏論的に定義したものとして、ウヴェ・フランツの論文があります。

• Title: What is Stochastic Independence? (3 Jun 2002)
• Author: Uwe Franz
• Pages: 17p
• URL: https://arxiv.org/abs/math/0206017

フランツによる統計的独立性の定義は、2つの確率空間（台集合、σ代数、確率測度の3つ組） (X, Σ_X, μ_X), (Y, Σ_Y, μ_Y) のテンソル積 (X×Y, Σ_XΣ_Y, μ_Xμ_Y) に基づいています。フランツの独立性は、必ずしも統計的独立性に限定はされませんが、「テンソル積〈モノイド積〉ありき」から出発します。

統計的独立性の定義が、いつでもテンソル積に基づいているわけではありません。事象の独立性やσ代数の独立性から、確率変数の独立性を定義するのが普通です。むしろ、確率空間のテンソル積を正面から導入するほうが珍しい（あまりやらない）でしょう*1。

アレックス・シンプソンも、統計的独立性を含む一般的な独立性概念の圏論的な定式化を提案しています。

• Title: Category-theoretic Structure for Independence and Conditional Independence
• Author: Alex Simpson
• Pages: 17p
• URL: https://www.sciencedirect.com/science/article/pii/S1571066118300318

シンプソンの独立性は、テンソル積〈モノイド圏のモノイド積〉を使っていません。「個々のケースごとに独立性をどう定義すべきか？」という問題意識ではなくて、「一般的に「独立性」と呼ばれる性質を、できるだけ抽象的に捉えたい」という動機からの定式化です。

この記事では、シンプソンの定義（を多少変更したもの）に基づいて、統計的独立性と線形独立性を一様に説明できる枠組みを構成します。

線形独立性

話を簡単にするために、ベクトル空間は実数体R上の有限次元ベクトル空間に限ります*2。有限次元のR-ベクトル空間と線形写像の圏を FdVect_R とします。ベクトル空間のテンソル積（モノイド構造）は考えません。

ベクトル空間Vの部分集合A（A⊆V）の線形独立性はご存知でしょう。単一の部分集合ではなくて、2つの部分集合 A, B⊆V に対して、AとBが線形独立であることを次の条件（すべて満たす）で定義します。

1. AはV内で線形独立である。
2. BはV内で線形独立である。
3. Aが生成するVの部分ベクトル空間と、Bが生成するVの部分ベクトル空間の共通部分はゼロだけ。

この線形独立性の定義をもう少し扱いやすくしましょう。そのために、集合から生成された自由ベクトル空間を使います。集合Aから生成された自由ベクトル空間を R[A]₁ とします。この記号のココロは、Aを不定元集合として生成された実係数多項式の集合 R[A] の（同次の）1次式部分ということです。

ベクトル空間Vに対して A, B⊆V ならば、次の写像達が誘導されます。（使っている概念・記号に関しては、この節最後の補足コラムで説明しています。）

1. 包含写像 i:A→V
2. 包含写像 j:B→V
3. iとjのコタプル写像 [i, j]:(A + B)→V
4. iに伴う線形写像 i_#:R[A]₁→V
5. jに伴う線形写像 j_#:R[B]₁→V
6. i_#とj_#のコタプル線形写像 [i_#, j_#]:R[A]₁R[B]₁→V

また、集合AとBの直和を A + B と書けば、次のベクトル空間の同型が成立します。

• R[A]₁R[B]₁ R[A + B]₁

よって、上記の最後のコタプル線形写像は、R[A + B]₁→V とみなすこともできます。

さて、A, B⊆V が線形独立であることは、コタプル線形写像を用いて次のように表現できます。

• コタプル線形写像 [i_#, j_#]:R[A]₁R[B]₁→V が単射である。

より一般に、A₁, ..., A_n⊆V に対して、これらが線形独立であることを次のように定義します。

• コタプル線形写像 [(i₁)_#, ..., (i_n)_#]:R[A1]₁ ... R[A_n]₁→V が単射である。

単一の部分集合 A⊆V に対しては、

• 線形写像 i_#:R[A]₁→V が単射である。

となり、部分集合の個数に関係せずに、幾つかの部分集合達の線形独立性が定義できます*3。

[補足]
集合AとBの直和は、「共通部分〈交わり〉なしの合併」と考えればいいのですが、具体的な定義が欲しいときは：

• A + B := {(x, i)∈(A∪B)×{1, 2} | (x∈A かつ i = 1) または (x∈B かつ i = 2)}

この具体的な定義を使うことにして、f:A→X と g:B→X のコタプル写像 [f, g]:(A + B)→X は：

• [f, g](x, i) := if (i = 1) then f(x) else /* i = 2 */ g(x) endif

包含写像とは恒等写像を部分集合に制限したものなので、i, j が包含写像なら：

• [i, j](x, i) := if (i = 1) then x else /* i = 2 */ x endif

Vはベクトル空間として f:A→V の線形拡張 f_#:R[A]₁→V は：

• f_#(Σ_a∈A ξ_aa) := Σ_a∈A ξ_af(a) （ξ_a∈R）

線形写像 φ:U→V と ψ:W→V のコタプル線形写像 [φ, ψ]:UW→V は：

• [φ, ψ](u, w) := φ(u) + ψ(w)

[/補足]

コスパン独立性

前節で、ベクトル空間Vの部分集合達 A₁, ..., A_n が線形独立であることを定義しました。線形独立性の定義には、n個の線形写像 (i₁)_#:R[A₁]₁→V, ..., (i_n)_#:R[A_n]₁→V が使われました。であるならば、n個の線形写像 f₁:U₁→V, ..., f_n:U_n→V に対して線形独立性を定義してもいいでしょう。

余域がVであるn個の線形写像 f₁:U₁→V, ..., f_n:U_n→V が線形独立であるとは：

• コタプル線形写像 [f₁, ..., f_n]:U₁ ... U_n→V が単射である。

「独立である」の主語は、n個の集合からn個の線形写像に変化しています。さらに、線形写像を一般的な射に置き換えることにより、任意の圏C上の独立性構造〈independence structure〉を定義します。「独立である」の主語は、n個（むしろn本）のCの射になります。ただし、それらの射の余域は同一です。

Cを圏として、同一の余域を持つn本の射のリスト (f₁:A₁→B, ..., A_n→B) をn-コスパン〈n-cospan〉と呼びます。n = 0, 1 の場合、つまり (), (f:A→B) もコスパンとして認めます。射を矢印で描くと、n-コスパンは、ひとつの点に合流する矢の並びになります。n = 0 のときは、先端点である対象Bだけがあると考えます。

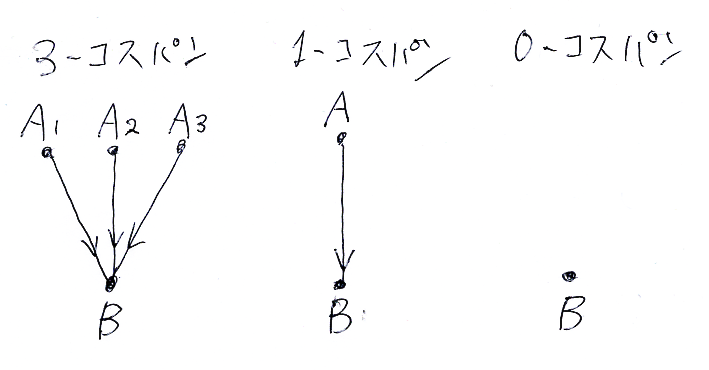
圏Cの、“対象Bを余域とするn-コスパン”の全体を Cosp_n(C, B) と書きます。Cが小さい圏でないなら、Cosp_n(C, B) は集合（小さい集合）とは限らず、真クラス〈proper class〉になるかも知れません。なので、「クラス」という言葉を使いますが、サイズの問題はあまり気にしません。次の記号も使います。

• Cosp(C, B) := (n∈N | Cosp_n(C, B))
• Cosp_n(C) := (B∈Obj(C) | Cosp_n(C, B))
• Cosp(C) := (n∈N, B∈Obj(C) | Cosp_n(C, B))

Cosp(C)は、圏Cのすべてのコスパンのクラスです。

コスパンを構成する射を識別するインデックスには、通常は自然数 1, 2, ..., n を使いますが、任意の有限集合をインデックスセットに許したほうが便利です。コスパンを (f_i | i∈I) のように書いたとき、Iは必ずしもNの部分集合とは限らない有限集合だとします。

圏Cのすべてのコスパンのクラス Cosp(C) の部分クラスを、X, Y などの斜体文字で表すことにします。以下、X, Y などは（圏C上の）コスパンのクラスです。

圏C上のコスパンのクラスXが次を満たすとき、Xはインデックスセットの全単射取り替えに対して安定〈stable under bijective change of index-set〉といいます*4。

• (f_i:A_i→B | i∈I)∈X、τ:J→I が全単射のとき、(f_τ(j):A_τ(j)→B | j∈J)∈X

今後考えるコスパンのクラスは、常にインデックスセットの全単射取り替えに対して安定だとします。別な言い方をすると、射のリストの並び順は気にしなくてもいいことになります（無視はしないほうがいいけど）。

圏C上のコスパンのクラスX（インデックスセットの全単射取り替えに対して安定は前提）が次を満たすとき、Xは複圏〈multicategory〉をなすといいます。

1. 任意の対象 A∈|C| に対して、単一射からなるコスパン (id_A)∈Cosp₁(C, A) は X に属する。
2. (g:B_j→C | j∈J)∈X、j∈J ごとに、(f_j,i:A_j,i→B_j | i∈I_j)∈X、このとき、(f_j,i;g_j:A_j,i→C | (j, i)∈Σ(j∈J | I_j)) 。

二番目の条件は、木の接ぎ木結合〈grafting〉に対して閉じていることです。接ぎ木結合は、m本の枝を持つ木gとm本の木f_i（合計(m + 1)本の木）に対して、gの各枝にf_iの根を接合して大きな木を作ることです。

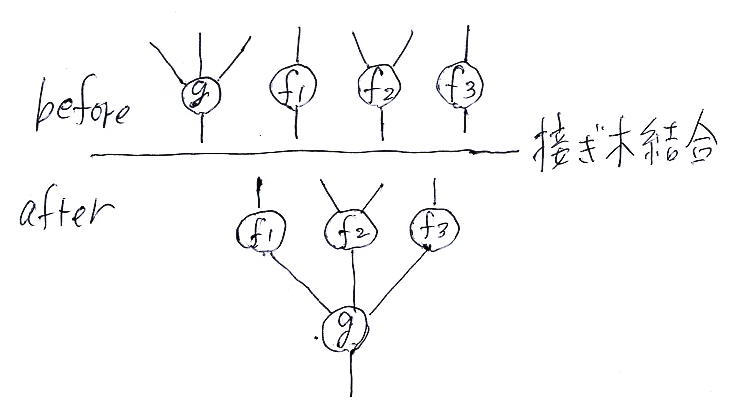
ちなみに、今定義した複圏の構造は、対称色付きオペラッド〈symmetric coloured operad〉とも呼びます。

R上の有限次元ベクトル空間の圏FdVect_Rにおいて、線形独立なコスパン (f_i:U_i→V | i∈I) の全体をXとすると*5：

1. Xは、インデックスセットの全単射取り替えに対して安定。
2. Xは、複圏をなす。

さらに、Xはインデックスセットの全単射取り替えに対する安定性より強い性質を持ちます。それは：

• (f_i:U_i→V | i∈I)∈X、τ:J→I が単射のとき、(f_τ(j):U_τ(j)→V | j∈J)∈X 。

全単射だけではなくて、インデックスセットの単射取り替えに対する安定性〈stability under injective change of index-set〉を持ちます*6。

一般に、圏C上のコスパンのクラスCosp(C)の部分クラスXが指定されており、Xがインデックスセットの単射取り替えに対して安定な複圏構造を持つとき、XをC上のコスパン独立性構造〈cospan independence structure〉と呼びます。コスパン独立性構造をコスパン独立性とも呼びます。誤解の恐れがなければ、単に独立性ともいいます。

FdVect_R上の線形独立なコスパンの全体は、コスパン独立性構造の事例です。

スパン独立性

シンプソンの論文における独立性は、前節のコスパン独立性に対して、「矢印の向きを反対にする」という意味で双対的なものです。

Cを圏として、同一の域を持つn本の射のリスト (f₁:A→B₁, ..., A→B_n) をn-スパン〈n-cospan〉と呼びます。圏Cの、“対象Aを域とするn-スパン”の全体を Span_n(C, A) と書きます。次の記号も使います。

• Span(C, A) := (n∈N | Span_n(C, A))
• Span_n(C) := (A∈Obj(C) | Span_n(C, A))
• Span(C) := (n∈N, A∈Obj(C) | Span_n(C, A))

圏C上のコスパンのクラスXに対して、Xはインデックスセットの全単射取り替えに対して安定〈stable under bijective change of index-set〉であることも前節と同様に定義します。

複圏の双対概念を余複圏〈comulticategory〉として、クラスXが余複圏をなすことも前節と同様です。木〈ツリー〉の向きが「葉から根」に対して「根から葉」の向きに変わります。

圏CのスパンのクラスXがスパン独立性構造〈span independence structure〉だとは：

1. Xは、インデックスセットの全単射取り替えに対して安定。
2. Xは、余複圏をなす。
3. (f_i:A→B_i | i∈I)∈X、τ:J→I が単射のとき、(f_τ(j):A→B_τ(j) | j∈J)∈X 。

三番目から一番目は出るので、冗長な条件になっていますが、このほうが分かりやすくでしょう。スパン独立性構造をスパン独立性とも呼びます。誤解の恐れがなければ、単に独立性ともいいます。

シンプソンの独立性は、もうひとつ条件が加わっています。それは：

• 任意の射 f:A→B に対して、単一の射からなるスパン (f:A→B) はXに所属する。

この条件をシングルトン条件〈singleton condition〉と呼びましょう。このシングルトン条件を独立性構造の定義に入れなかったのは、前節の線形独立性がシングルトン条件を満たさないからです。コスパン独立性、スパン独立性を広い範囲で考えたいなら、シングルトン条件は追加・削除が可能な形にしておいたほうが良さそうです。

確率空間と確率測度を保存する可測写像の圏をProbとすると、確率変数（＝確率測度を保存する可測写像）の独立性は、圏Prob上のn-スパン (f₁:A→B₁, ..., f_n:A→B_n) のスパン独立性になります。単一の確率変数からなる1-スパン (f:A→B) は独立とみなすので、圏Prob上の（標準的な）スパン独立性はシングルトン条件を満たします。

コスパン生成性とスパン生成性

コスパン独立性とスパン独立性は互いに双対の関係になります。これとは別な双対性があります。コスパン独立性の別な双対としてコスパン生成性、スパン独立性の別な双対としてスパン生成性を考えましょう。

コスパン生成性は、線形独立性に対する線形生成性から思い付いたものです。まずは、線形生成性から説明します。線形写像 f:U→V が線形生成〈linear generation〉だとは、fが全射であることだと定義します。部分集合 A⊆V が生成系〈generating system〉であるとき、包含写像の線形拡張 R[A]₁→V は線形生成（つまり全射）になります。

圏FdVect_R上のn-コスパン (f_i:U_i→V | i∈I) が線形生成であることは、コタプル写像 [f_i | i∈I]:(_i∈IU_i)→V が全射であることだと定義します。

圏FdVect_R上の、すべての線形生成コスパンからなるクラスXは次の性質を持ちます。

1. Xは、インデックスセットの全単射取り替えに対して安定。
2. Xは、複圏をなす。
3. (f_i:U_i→V | i∈I)∈X、τ:J→I が全射のとき、(f_τ(j):U_τ(j)→V | j∈J)∈X 。

線形独立コスパンのクラスとの違いは、インデックスセットの（単射ではなくて）全射取り替えに対して安定していることです。

線形生成コスパンのクラスを一般化して、圏C上のコスパン生成性構造〈cospan generation structure〉を定義できます。その定義はもう明らかでしょう。矢印を逆転させる双対をとって、圏C上のスパン生成性構造〈span generation structure〉も定義できます。

次の4つの構造は双対性で互いに結び付けられているので、一緒に考えたほうがいいと思います。

1. コスパン独立性構造
2. スパン独立性構造
3. コスパン生成性構造
4. スパン生成性構造

*1:潜在的には、確率空間のテンソル積を使っていることになりますが。

*2:今回の話では、有限次元じゃなくても難しくはなりません。気分的に簡単な印象があるだけです。

*3:定義から分かるように、A₁, ..., A_n の線形独立性は、単一の集合 A₁∪ ... ∪A_n の線形独立性に帰着されます。その意味では、複数の集合に関する線形独立性が必須とは言えません。

*4:シンプソンは、単に安定と呼んでいます。

*5:線形独立なコスパンは、jointly monic cospan です。関連する話題が「余関係＝関係の双対概念」にあります。

*6:シンプソンは、この安定性をアフィン〈affine〉と呼んでいます。