随伴系の二重圏

ひとつ前の記事「随伴系の圏の多様性」にて：

₁Adj_L(Cat)（あるいは、₁Adj_R(Cat)）だけでも、モナド／コモナドを調べる道具に使えます。が、やはり随伴系の二重圏が欲しい。というわけで、随伴系の二重圏についても述べたいとは思っています（いつかわからんが）。

随伴系の二重圏は色々と使い途があるので、早めに定義しておきます。

内容：

形式論と具体論

モナドや随伴の理論には、形式論〈formal theory〉と具体論〈concrete theory〉があります。「最近のモナド論の概観と注意事項 1/2 // モナド論を分類すれば」では、形式論と“非形式論”という言葉を使ったのですが、ここでは具体論にします。

形式論は、一般的な厳密2-圏（または弱2-圏＝双圏）Kを舞台として理論を展開します。それに対して、具体論は K = Cat と固定した理論になります。この記事では、主に具体論を扱いますが、ほとんどは形式論でも通用する話です。形式論の用語もけっこう使います。念の為に、「形式論 vs. 具体論」の対応表を載せておきます。

形式論	具体論
K	Cat
対象＝0-射	圏
射＝1-射	関手
2-射	自然変換

形式論におけるモナド／随伴系を、形式モナド／形式随伴系と言う人もいますが、そこまで区別するのは面倒だし意味もないと思うので区別しません。

厳密2-圏K内のモナドの全体を Mnd(K)、随伴系の全体を Adj(K) と書きます。しかし、モナドの全体も随伴系の全体も色々な種類があるので、'Mnd'と'Adj'に対して左下付きと右下付きで様々な修飾をします（「最近のモナド論の概観と注意事項 2/2」と「随伴系の圏の多様性」参照）。

上下左右の使い方

圏論、特に高次圏論の学習では、“上下左右”に慣れることが肝だと思います。なので、上下左右の話は、何度も何度も何度も繰り返しています*1。比較的最近だと：

• カン拡張における上下左右： 入門の前に整理すべきこと

その後の記事でも再度注意しています。

• カン拡張のために、柱の絵を描く // 再び上下左右に関する注意

随伴系に関して言えば、2つの関手が構成素〈constituent | ingredient〉として含まれます。その2つの関手の片方を左関手と呼び、もう一方を右関手と呼びます。「左右」は単にペア〈カップル | コンビ〉における役割を区別するだけなので、「左関手・右関手」の代わりに「妻関手・夫関手」でも「ボケ関手・ツッコミ関手」でもかまいません。（次の記事も参照。）

• 圏論の随伴をちゃんと抑えよう // 左と右を忘れるんだが
• 随伴に関する注意事項

一方で、図（ペースティング図とストリング図）を描いたとき、ほんとの空間的な位置・方向として上下左右を使うこともあります。さらには、空間的位置・方向にちなんで用語〈テクニカルターム〉が決められることもあります。ところがさらに、図の描き方（描画方向）が多様なので、描き方を変えると空間的位置・方向と用語は一致しなくなります。

「圏論の極限を具体的に // 関手の極限の復習」に挙げた例ですが、次の圏論用語は同義語（「右カン拡張」は類義語）です。

• 極限＝逆極限＝左根≒右カン拡張

もうほんとにどうにもならないグチャグチャ状況で、改善は無理でしょう。やれることは、注意して混乱や誤解を避けることだけ。今回の二重圏の話では、上下左右の議論がウンザリするほど登場します。ご注意ください。

2-射の形状

この記事では、圏を対象として随伴系を水平射として、関手を垂直射とする二重圏〈double category〉を考えます。二重圏やその実例については、次の記事に書いてあります。

• 二重圏における交替律
• 二重圏の具体的な定義
• 二重圏の簡単な例：非負行列の順序構造
• 二重圏のもっと簡単な例：圏の可換四角形の二重圏

随伴系の二重圏と言っても、作り方のオプションがいっぱいあるのですが、とりあえずは曖昧かつ総称的に、単に「二重圏」と呼んでおきます。

二重圏で注目すべきはその2-射〈2-セル〉です。2-射の図は2次元的な四角形になります。ここから先の説明で出てくる「上下左右」は、基本的には空間的な位置・方向のことです。ただし、左関手／右関手、（後で出てくる）左自然変換／右自然変換の「左右」は役割を識別する「左右」です。水平射を左から右、垂直射を上から下に描くことにします。

この描画方向で、二重圏の2-射αは次のようになります。

 C --(A)-→ D
 |         |
(F)   α   (G)
 |         |
 v         v
 C' -(A')→ D'

AとA'はそれぞれ随伴系で、水平射としての方向は随伴系の左関手の方向に合わせています。A = (η, ε: L -| R, L:C→D), A' = (η', ε': L' -| R', L':C'→D') とすれば、方向は次のようです：

• A:C→D は、L:C→D と同じ方向。R:D→C とは逆方向。
• A':C'→D' は、L':C'→D' と同じ方向。R':D'→C' とは逆方向。

もちろん、随伴系の方向を右関手の方向に合わせても何の不都合もなく、水平射の方向の選択はまったく恣意的です。

二重圏の2-射αは、実は2つの自然変換（もとにする厳密2-圏Catの2-射）から構成されます。α = (α_left, α_right) とします。α_leftとα_rightが何モノであるか分かるように絵を描くと：

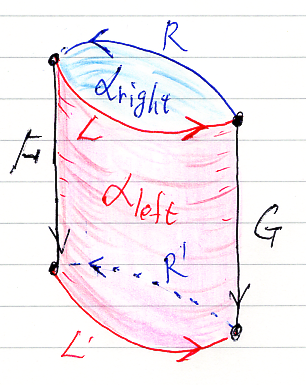
α_leftは、上下辺が左関手LとL'である四角形（図のピンクの四角形）として描かれます。なので、左自然変換〈left natural transformation〉と呼ぶことにします。左関手／左自然変換の「左」は空間的位置・方向ではなくて、役割を識別する形容詞です。同様に、上下辺が右関手RとR'である四角形（図で奥側の水色の四角形）として描かれる自然変換は右自然変換〈right natural transformation〉です。左自然変換と右自然変換のペアが二重圏の2-射を構成します。

2-射αの構成素である左自然変換α_leftを考えると、その方向の選び方は二種類あります。

1. α_left: F*L'⇒L*G （下図の左側）
2. α_left: L*G⇒F*L' （下図の右側）

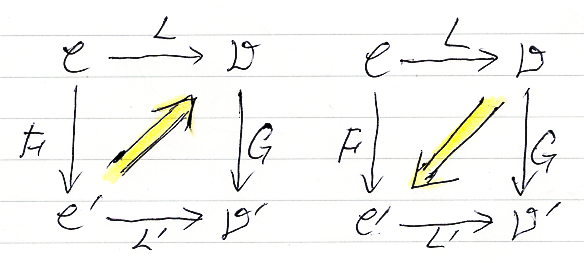
一番目の方向を（地図の方向から）北東〈North-East〉方向、二番目の方向を南西〈South-West〉方向と呼ぶことにします。

2-射αの右自然変換α_rightの方向の選び方も同様に2つの方向があります。

1. α_left: R*F⇒G*R' （下図の左側）
2. α_left: G*R'⇒R*F （下図の右側）

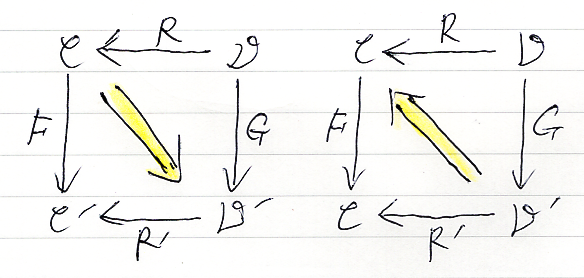
ただし、この図では、随伴系の右関手 R, R' のアローの方向が右から左になっています。通常の左から右にすれば、自然変換の方向も変化して見えます。我々は、右関手を逆向きに描くこの描画法を採用します。最初の立体的な絵において、左自然変換の面を正面に見る方向から観測して描いていると思ってください（裏側からは見ない）。図の左側が南東〈South-East〉方向、図の右側が北西〈North-West〉方向です。

α_left, α_rightの方向の組み合わせは4種類になります。

1. α_leftが北東方向、α_rightが南東方向
2. α_leftが北東方向、α_rightが北西方向
3. α_leftが南西方向、α_rightが南東方向
4. α_leftが南西方向、α_rightが北西方向

しかし、とある条件（次節）を付けてふるい落とすと一種類だけが残ります。左自然変換が北東方向、右自然変換が南東方向が我々が使う組み合わせです。最初に選ぶ随伴系の方向を右関手に合わせると、右自然変換が南西方向、左自然変換が北西方向になります。とある条件については、次節で説明します。

メイト

前節で多様な方向について述べました。随伴系の方向の選び方が2種あり、それぞれについて、二重圏の2-射（＝左自然変換と右自然変換のペア）の方向の選び方が4種あるので、二重圏としての方向の選び方は8種あり、方向の定義が異なる8つの二重圏が出来ます。

しかし、モナドと随伴系の関係を調べる目的では、8つの二重圏は無駄に一般的過ぎるようです。モナド論のなかでは、2-射の左自然変換と右自然変換が無関係である場合は出現しないからです。2-射の左自然変換と右自然変換には次の条件を課します。

• 2-射を構成する左自然変換と右自然変換は、互いにメイト〈mate〉である。

今からメイトの説明をしますが、「互いにメイト」の特殊ケースでよく知られたものがあります。紹介しておきます。

1. 随伴系によるホムセットの同型 D(L(A), Y) C(A, R(Y)) により、射 g:L(A)→Y と f:A→R(Y) が互いに転置になる。
2. ベクトル空間のあいだの2つの線形写像 f:V→W と g:W^*→V^* が互いに双対になる。

「互いに転置」「互いに双対」は、「互いにメイト」の特殊ケースです。今日は、メイトの一般論とその特殊ケースの関係を論じることはしませんが、随伴系の転置、線形写像の双対については次の記事で述べています。

• 圏論の随伴をちゃんと抑えよう // 転置と反転置
• 圏論の随伴をちゃんと抑えよう： お絵描き完全解説 // 転置オペレータ／反転置オペレータとその描画
• 双対ベクトル空間、これくらい知ってればイインジャナイ // 双対線形写像
• 双対ベクトル空間、もう少し知っておいたほうがイイカモ // 「双対写像」の3つの用法

さて、メイトという言葉をどのように使うかを説明します。実際の定義は次節です。

• とある2つの自然変換の集合のあいだに1：1の対応がある。この対応をメイト対応〈mate correspondence〉、またはメイト同型〈mate isomorphism〉と呼ぶ。
• メイト対応で対応付けられる2つの自然変換は互いにメイト〈mate〉であるという。

メイト対応

A = (η, ε: L -| R, L:C→D) と A' = (η', ε': L' -| R', L':C'→D') を2つの随伴系とします。次のような自然変換の集合を考えます。

1. Nat(F*L', L*G:C→D') ： 関手 F*L':C→D' から関手 L*G:C→D' への自然変換の集合
2. Nat(R*F, G*R':D→C') ： 関手 R*F:D→C' から関手 G*R':D→C' への自然変換の集合
3. Nat(L*G, F*L':C→D') ： 関手 L*G:C→D' から関手 F*L':C→D' への自然変換の集合
4. Nat(G*R', R*F:D→C') ： 関手 G*R':D→C' から関手 R*F:D→C' への自然変換の集合

先に導入した左自然変換／右自然変換と、自然変換の地図的方向を使って表現すれば：

1. Nat(F*L', L*G:C→D') ： 北東方向の左自然変換の集合
2. Nat(R*F, G*R':D→C') ： 南東方向の右自然変換の集合
3. Nat(L*G, F*L':C→D') ： 南西方向の左自然変換の集合
4. Nat(G*R', R*F:D→C') ： 北西方向の右自然変換の集合

地図的方向は、左自然変換を正面に見る視点から観測して言ってることで、右関手は奥側を右から左に向かっています。

さて、メイト対応は、次のような対応です。

• Nat(F*L', L*G:C→D') ←→ Nat(R*F, G*R':D→C')

互いに逆写像であるペアなので、2つの写像があります。それらは、絵（ストリング図）を使えば簡単で印象的に表せます。

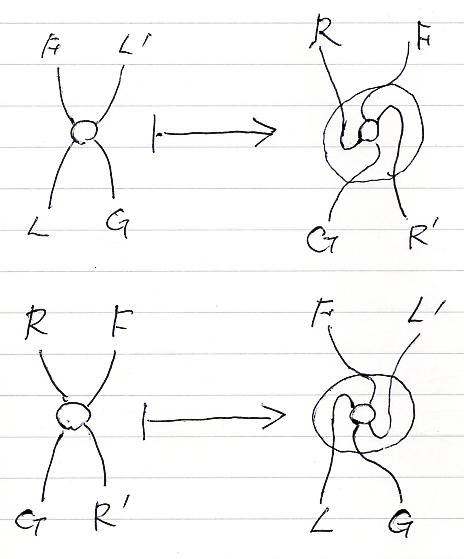
写像に名前を付けるより、次のような象形文字風の演算子記号を使うと分かりやすいでしょう。

• _∪(-)^∩:Nat(F*L', L*G:C→D')→Nat(R*F, G*R':D→C')
• ^∩(-)_∪:Nat(R*F, G*R':D→C')→Nat(F*L', L*G:C→D')

_∪(-)^∩ と ^∩(-)_∪ が互いに逆なのは、随伴のニョロニョロ関係式〈snake relation〉から明らかです。

Nat(L*G, F*L':C→D') と Nat(G*R', R*F:D→C') のあいだでは、随伴系の単位・余単位を使ったメイト対応がうまく定義できないことが（やってみれば）分かります。随伴は完全な対称性は持ってないのですよね。ただし、（ストリング図で言えば）左右のワイヤーを交換するノードがあれば、メイト対応もどきが定義できるかも知れません（未確認）。

互いにメイトである自然変換のペアをメイトペア〈mate pair〉と呼ぶことにします。メイトペアの相方〈パートナー〉を求めるには、演算子 _∪(-)^∩ または ^∩(-)_∪ を適用すれば済みます。

二重圏としてのAdjの定義

メイトペアの準備ができれば、随伴の二重圏を定義できます。

まず、水平圏として ₁Adj_L(Cat) か ₁Adj_R(Cat) のどちらかを選びます。今は ₁Adj_L(Cat) を選んだとしましょう。2-射は、互いにメイトになっている左自然変換と右自然変換のペアを選びます。こうして作った二重圏を次のように書きます。

• _dAdj_L(Cat)

水平圏を ₁Adj_R(Cat) に選ぶと、次の二重圏ができます。

• _dAdj_R(Cat)

_dAdj_L(Cat) と _dAdj_R(Cat) の2-射の状況は、次のように図示できます。バッテンに交差した2本の二重矢印は、互いにメイトである自然変換を表します。

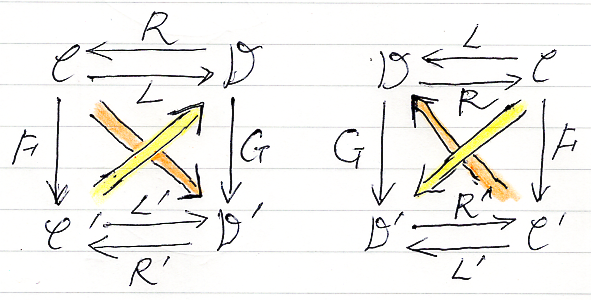
_dAdj_L(Cat), _dAdj_R(Cat) が二重圏の公理を満たすことを確認する必要がありますが、ペースティング図かストリング図を使えば容易に確認できます。

二重圏Adjの利用

今回定義したような随伴の二重圏は、1960年代後半には、パルムクイスト〈Paul H. Palmquist〉*2により調べられていたようです。（紙の出版物でしかアクセスできないので、実物は見てません。）

• Paul H. Palmquist. The Double Category of Adjoint Squares. PhD thesis, University of Chicago, 1969.

メイト対応を含めた随伴系の全体を把握するために、二重圏に編成するのはとても良いアイデアだと思います。二重圏の基本理論を適用して、随伴系達の構造がハッキリと見えるようになります。

二重圏を定義する場合、随伴系を水平射とするか垂直射とするかもオプションなので、随伴系を垂直射とした定義もあります。当然ながら、上下左右の話は丸っきり変わってしまいます。（が、本質的には同じこと。）

具体的な厳密2-圏Catをベースに話をしましたが、一般的・抽象的な厳密2-圏Kに対しても二重圏 _dAdj_L(K), _dAdj_R(K) を定義できます。さらには、弱2-圏〈双圏〉Kに対しても同様な議論ができます。

「メイト」の節でちょっと触れたように、双対ベクトル空間／双対線形写像は、単対象弱2-圏とみなした Vect_K（Kは適当なスカラー体）に対する _dAdj_L(Vect_K) を使って定式化できます。

そしてもちろん _dAdj_□(K)（右下の'□'には'L'か'R'が入る） は、モナドと随伴系の関係を調べるときの基本的な道具になります。モナドの圏は、_dAdj_□(K) に埋め込むことができます。

_dAdj_□(K) に、さらに3-射を加えて3次元の圏を作れます。この3次元構造は、モナドの2-射（モナドのあいだの射のあいだの射）を調べるときに必要となります。

また、_dAdj_□(K) は、二重圏の事例としても面白いと思います。パラメータKを変えれば様々な二重圏を作れるので、事例の供給源になりそうです。

*1:自分（檜山）が上下左右のような空間認識が苦手で苦労しているので、過度に強調しているかも知れません。

*2:https://ja.forvo.com/search/Palmquist/ によると、"Pa"は「パ」とは発音しないようですが、うまくカタカナ表記できないし、綴りが連想できるように「パ」にしました。