このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

線形近似としての微分係数： フレシェ微分

雑記／備忘

関数fの点aにおける微分係数は、a近辺でfを良く近似する線形写像（正確にはアフィン線形写像の線形部分）とみなせます。線形近似としての微分の一般的な形はフレシェ微分〈Fréchet {derivative | differential}〉といいます。

フレシェ微分の枠組みでは、“一実数変数・実数値の関数”でも“（無限次元でもよい）ノルム空間のあいだの写像”でも扱いは変わらないので、一般的な話をしてみます。もちろん、一実数変数・実数値の関数でも通用する話です。

内容：

はじめに

この記事は2回の続き物を予定しています。次回がいつか分かりませんが(苦笑)。なぜ2回に分けようとしたかを説明します。

一実数変数・実数値の関数を扱う場合でも、f:R→R という関数だけではなくて、XをRの開区間として f:X→R、あるいはYもRの開区間として f:X→Y という形の関数も対象にします。R全体ではなくて、Rの部分集合で定義されている関数も必要なのです。

ところが、「全体ではなくて部分集合で」だと、話が面倒になってしまうところがあります。そこで今回は、「全体で」定義された関数に話を限定します。「部分集合で」は次回にします。微分公式もチェーン法則〈chain rule | 合成関数の微分公式〉だけを取り上げ、その他の微分公式は次回にします。

一般的な設定で話をしますが、「ノルム空間」という言葉が出てきたらそれを「実数全体の集合（＝R）」に置き換え、「ノルム」を「絶対値」に置き換えて読めば、一実数変数・実数値のケースになります。一般的な場合と簡単（一実数変数・実数値）な場合の対応は：

一般的な場合 簡単な場合
ノルム空間 実数全体の集合
ノルム 絶対値
線形写像 正比例関数
アフィン線形写像 1次関数

フレシェ微分については、ジョーダン・ベルの論説に要領よくまとまっています。

アフィン線形近似

U, V はノルム空間〈normed spaces〉とします。ノルム空間を知らなければ、U = V = R と考えてください。f:U→V は連続写像とします。以下、連続写像しか考えません。なお、「写像」と「関数」という言葉は完全な同義語として使い、どっちを使うかは気分次第です。

A:U→V は線形写像とします。線形写像も連続なものだけを考えます（無限次元のノルム空間では、連続でない線形写像も存在します）。線形写像Aに関しては、A(x) を単に Ax とも書きます。線形写像に大文字を使ったのは、行列をイメージすればいいからです。U, V が Rn, Rm のケースでは、線形写像Aは、m行n列の行列と同一視できます。n = m = 1 なら、Aは1個の数（スカラー）による掛け算（＝正比例関数）です。

次の形の写像 ℓ:U→V をアフィン線形写像〈affine linear map〉、または単にアフィン写像〈affine map〉と呼びます。

  • x∈U に対して、ℓ(x) = b + A(x - a)
  • a∈U, b = ℓ(a) ∈V, A:U→V は（連続な）線形写像

x - a を uと置くと、u = x - a, x = a + u なので：

  • u∈U に対して、ℓ(a + u) = b + Au
  • a∈U, b = ℓ(a) ∈V, A:U→V は（連続な）線形写像

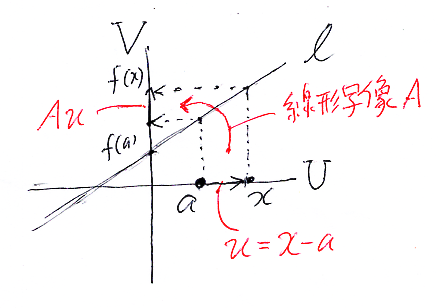
この状況で、xは点を表す変数、aは定点を表す定数、uはa周辺の変位ベクトルを表す変数と考えます。

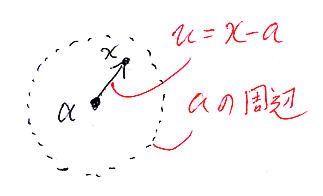
一般の連続写像 f:U→V を、アフィン線形写像 ℓ:U→V で近似することを考えます。雰囲気的には：

  • f(x) ≒ ℓ(x) = b + A(x - a)

あるいは、

  • f(a + u) ≒ ℓ(a + u) = b + Au

アフィン線形写像の定数項bをf(a)にとれば、f(a) = ℓ(a) になるので、b = f(a) とします。

近似アフィン線形写像ℓともとの写像fの差をとります。

  • p(u) := f(a + u) - ℓ(a + u)

aの周辺だけを問題にしているので、近似誤差を表す関数pの変数はxではなくてu（aのまわりを動く局所的な変数）を使います。p(0) = f(a) - ℓ(a) = f(a) - b = 0 なので、u = 0 （x = a）においてfとℓの値は一致しています。つまり、0次近似は完全に（誤差なく）出来ています。

“近似関数ℓ”と“もとの関数f”との“a周辺での差”であるpは、"remainder"と呼ばれます。"remainder"は「剰余項」と訳されるようですが、割り算の余りのイメージが強いので、残余項、または単に残余とします。良い近似とは、残余が小さい近似ということになります。

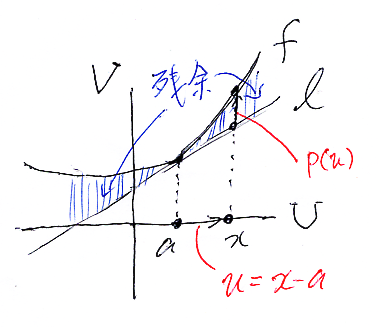
スモールオー関数

良い近似は残余が小さい近似です。ここで「小さい」をハッキリさせます。「小さい」は、雰囲気的には「ゼロに近い／ほとんどゼロ／無いに等しい」とか言ってもいいでしょう。この雰囲気は、次のスモールオー関数により定式化できます。

p:U→V がスモールオー〈small-o | little-o〉であるとは：

  1. pは連続関数
  2. p(0) = 0
  3. |u| → 0 のとき、|p(u)|/|u| → 0

ベクトル（ノルム空間の要素）のゼロもスカラー（Rの要素）のゼロも同じ'0'で書いているので注意してください。三番目の条件は、極限に関するもので、uのノルム（普通の絶対値記号を使っています）が0に近づくとき、p(u)のノルムとuのノルムの比が0に近づくことを意味します。f(x) = x2 : R→R はスモールオーな関数で、f(x) = x : R→R はスモールオーな関数ではありません。

「近づく」は不正確に思えますが、次の論理式の略記だと思えば厳密な意味を持ちます。（R>0は、正の実数の集合です。）

  • ∀δ∈R>0.∃δ∈R>0.(|u| < ε ⇒ |p(u)|/|u| < δ)

極限・収束に関するこのような表現方法については、次の記事を参照してください。

'∀'と'∃'に慣れてなかったら、次の記事を読むといいでしょう。

スモールオーという呼び名は、ランダウのスモールオー記号にちなんだものです。pがスモールオーであるとは、値p(u)が変数uよりも速くゼロに近づくことです（雰囲気は）。さらに雰囲気的で古臭い言い方をするなら、「uが無限小のとき、p(u)は“高位の無限小”である」となります。「無限小」や「高位の無限小」は意味不明ですが、無限小自体を合理化しようとは意図してないので気にしないでください。

冒頭の節で紹介したベルの論説では、スモールオー関数を残余〈remainder〉と呼んでますが、ちょっと混乱しそう*1なので、スモールオーであることと残余（近似関数ともとの関数の差）であることは区別します。

有界線形写像

この節は、無限次元のノルム空間の場合の話で、U = Rn, V = Rm のときは気にする必要がないので飛ばしてもかまいません。ただし、線形写像 A:Rn→Rm のノルムの定義だけは必要です（すぐ下に書きます）。

線形写像 A:Rn→Rm に対して、単位球体 {x∈Rn | |x| ≦ 1} の像集合 {y∈Rm | ∃x∈Rn.(|x| ≦ 1 かつ y = Ax)} の“最大半径”をAのノルム〈norm of A〉と呼び、|A| と書きます。|A| = α と置くと、次が成立します。

  • |u| ≦ 1 ならば、|Au| ≦ α
  • 0 < β < α であるβ（そういうβがあれば）に対して、|u| ≦ 1 かつ |Au| > β となるuが存在する。

これが、「単位球体の像の最大半径」の実質的な意味です。

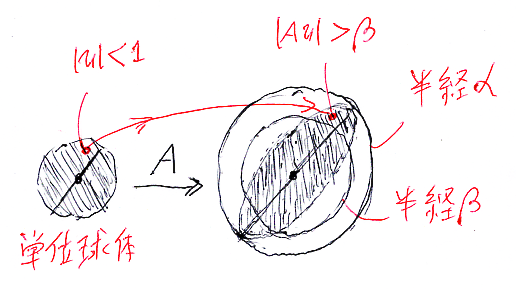
n = m = 1 で、A:R→R のとき、線形写像Aのノルム|A|は、正比例関数Aの比例定数の絶対値です。

さて、有限次元とは限らないノルム空間での話をします。ノルム空間Uの、aを中心として半径αの開球体を B(U, a, α) と書くことにします。開球体〈open ball〉でも閉球体〈closed ball〉でもどっちでもいいのですが、開球体だと別の目的（位相の開基）でも使えるので、開球体を使います。開球体／閉球体の別により、不等式のイコールの部分がちょっと違ってきます。

  • B(U, a, α) := {x∈U | |x - a| < α}

開球体の中心が原点（ゼロベクトル）0のときは、単に B(U, α) とも書きます。

  • B(U, α) := B(U, 0, α)

線形写像 A:U→V が有界〈bounded〉とは、単位開球体 B(U, 1) のAによる像が有界なことです。つまり、適当な正実数定数βがあって、B(U, 1)のAによる像がVの原点から距離β以内に収まることです。

  • ∀u∈U.(|u| < 1 ⇒ |Au| < β)

AによるB(U, 1)の像を A*(B(U, 1)) と書けば、次でも同じです。

  • A*(B(U, 1)) ⊆ B(V, β)

Aが有界なので、実数の集合 {β∈R | A*(B(U, 1)) ⊆ B(V, β)} は空ではありません。なので、下限〈infimum | 最大下界 | greatest lower bound〉が存在します。その下限がAのノルムです。

  • |A| := inf {β∈R | A*(B(U, 1)) ⊆ B(V, β)}

UからVへの有界線形写像の全体を BL(U, V) とすると、BL(U, V) の足し算／スカラー倍と共に今定義したノルムを考えると、BL(U, V) は実際にノルム空間になります。

各種の関数空間

U, V をノルム空間として、UからVへの写像の全体 Map(U, V) は、写像の足し算／スカラー倍でベクトル空間になります。Map(U, V) は一般的過ぎてあまり意味がないのですが、有用な関数からなる部分空間があります。

  1. C(U, V) -- UからVへの連続写像の全体
  2. BL(U, V) -- UからVへの有界線形写像の全体
  3. o(U, V) -- UからVへのスモールオー関数の全体

これらはどれも、ベクトル空間になっています。つまり、足し算とスカラー倍で閉じています。BL(U, V) は前節で述べたようにノルム空間になっています。

s:U→V が安定関数〈stable function〉であることを次のように定義します。

  1. sは連続写像
  2. s(0) = 0
  3. 適当な正実数 ε, γ があって、|u| < ε ⇒ |s(u)| < γ|u| が成立する。

三番目は、|u|を十分小さくすれば、比 |s(u)|/|u| を定数γで抑えられることを意味します。sは、原点〈ゼロベクトル〉付近で伸縮率が矢鱈に大きくなるような写像ではありません。原点から離れた所での挙動は特に規定されていません。s(0) = 0 である連続写像でも、安定でないものがあります。例えば、f(x) = x×sin(1/x) : R→R は安定ではありません。

UからVへの安定関数の全体を Stbl(U, V) と書きます。Stbl(U, V) もベクトル空間になります。

C(U, V), BL(U, V), o(U, V), Stbl(U, V) がどんな関係かを、証明は後回しで述べておきます。スモールオー関数と安定関数の定義から、

  • o(U, V) ⊆ C(U, V)
  • Stbl(U, V) ⊆ C(U, V)

は自明に言えます。定義から直接は言えませんが、次も証明できます。

  • BL(U, V) ⊆ C(U, V)
  • C(U, V)∩L(U, V) = BL(U, V) （L(U, V) は、UからVへの連続かどうか分からない線形写像の全体）

したがって、o(U, V), Stbl(U, V), BL(U, V) は、ベクトル空間 C(U, V) の部分ベクトル空間です。次の包含関係があります。

  • o(U, V) ⊆ Stbl(U, V)

これを示しましょう。p:U→V をスモールオー関数とします。正実数δをどう選んでも、εをうまく選べば、|u| < ε ⇒ |p(u)| < δ|u| と出来ます。最初に選んだδをγと置けば、これは、安定関数の三番目の条件を満たすことになります。一番目と二番目の条件は定義から明らかです。よって、スモールオー関数sは安定関数です。

次の包含関係もあります。

  • BL(U, V) ⊆ Stbl(U, V)

これも示しましょう。A:U→V を有界線形写像で、|A| = α とすれば、|u| < 1 ⇒ |Au| < α が成立します。w = (1/α)u, u = αw と置けば、|αw| < 1 ⇒ |A(αw)| < α と書けます。|αw| < 1 ⇔ |w| < 1/α 、|A(αw)| < α ⇔ |Aw|α < α ⇔ |Aw| < 1 なので、|w| < 1/α ⇒ |Aw| < 1 が成立します。これは、ε = 1/α, γ = 1 と置いた安定関数の三番目の条件です。一番目と二番目の条件は定義から明らかなので、有界線形写像Aは安定関数です。

o(U, V) も BL(U, V) も Stbl(U, V) の部分ベクトル空間空間であることが分かりました。o(U, V) と BL(U, V) は、Stbl(U, V) 内で全然異なった部分空間になっています。このことを正確に言うと：

  • o(U, V)∩BL(U, V) = {0}

p:U→V がスモールオー関数で、有界線形でもあるとします。有界線形なので、ノルム |p| = α が定まり、|u| < 1 ⇒ |p(u)| < α が成立します。αがゼロでないと仮定して矛盾を導きましょう。

αがAのノルムであることから、0 < β < α であるβに対して、|u| < 1 かつ β < |p(u)| となる u∈U をとれます。そのようなuはゼロでないので（u = 0 だと β < |p(u)| とはならない）、β/|u| < |p(u)|/|u| 。正の実数εに対する εu というベクトルを考えて、ε → 0 とすると、|εu| → 0 だが、|p(εu)|/|εu| は β/|εu| = (β/ε)|u| より大きくなって0に収束することが出来ません。これは、pがスモールオーであることに矛盾します。

よって、α = |p| = 0 であり、p = 0 が結論できます。

部分ベクトル空間 o(U, V) と BL(U, V) は、ベクトル空間 Stbl(U, V) のなかで原点（ゼロベクトル＝ゼロ写像）しか共通部分がなく、異なった方向に広がっています。

良い線形近似とその一意性

U, V をノルム空間、f:U→V を連続写像、a∈U とします。ℓ:U→V を、ℓ(x) = f(a) + A(x - a) で定義されるアフィン線形写像とします。A:U→V は有界線形写像です。有界線形写像Aをデタラメに選ぶと、fとℓは似てないことになります。ℓがfを良く近似〈good approximate〉していることを、残余 p(u) = f(a + u) - ℓ(a - u) がスモールオーであることだと定義します。

  • p(u) = f(a + u) - ℓ(a - u)
  • f(a + u) = f(a) + Au + p(u)
  • p:U→V はスモールオー

このとき、（有界な）近似線形写像 A:U→V を点aにおけるfの微分係数〈differential coefficient〉と呼びます。

以上の定義だと、良い近似線形写像＝微分係数の一意性は分かりません。異なる2つの微分係数があるかも知れません。

実際には一意的であることを示しましょう。A, B:U→V を2つの良い近似線形写像＝微分係数だとすると：

  • f(a + u) = f(a) + Au + p(u), p∈o(U, V)
  • f(a + u) = f(a) + Bu + q(u), q∈o(U, V)

この2つの等式を引き算すると：

  • f(a) + Au + p(u) - (f(a) + Bu + q(u)) = 0

これより、

  • (A - B)u = (q - p)(u)

uはU上を任意に動けるので、

  • A - B = q - p

BL(U, V) も o(U, V) もベクトル空間だったので、(A - B)∈BL(U, V), (q - p)∈o(U, V) 。A - B = q - p より、(A - B)∈o(U, V) 。ところが、前節の結果より、BL(U, V)∩o(U, V) = {0} だったので、(A - B) = 0、つまり A = B 。

良い線形近似は一意に定まります。ですから、最良の線形近似〈best {approximate | approximation}〉と言ってもいいことになります。

スモールオー関数と安定関数の結合〈合成〉

U, V, W をノルム空間とします。p, q, s, t を次のような関数だとします。

  1. p∈o(U, V)
  2. q∈p(V, W)
  3. s∈Stbl(U, V)
  4. t∈Stbl(V, W)

これらを結合〈合成〉すると、次のような関数ができます。スモールオーの'o'と、写像の反図式順結合記号'\circ'が紛らわしいので注意してください。

  1. q\circp:U→W
  2. t\circs:U→W
  3. t\circp:U→W
  4. q\circs:U→W

これらの結合関数〈合成関数〉が、再びスモールオー関数または安定関数になるでしょうか？ 結論を言えば：

  1. q\circp∈o(U, W)
  2. t\circs∈Stbl(U, W)
  3. t\circp∈o(U, W)
  4. q\circs∈o(U, W)

表にまとめると次のようです。

結合 o Stbl
o o o
Stbl o Stbl

あるいは、次のようにも書けます。結合が反図式順なので左右が不自然で、スモールオー'o'と結合記号'\circ'がほんとに紛らわしいけど*2：

  1. o(V, W)\circo(U, V) ⊆ o(U, W)
  2. Stbl(V, W)\circStbl(U, V) ⊆ Stbl(U, W)
  3. Stbl(V, W)\circo(U, V) ⊆ o(U, W)
  4. o(V, W)\circStbl(U, V) ⊆ o(U, W)

これらの証明は後回しにして、応用としてチェーン法則〈合成関数の微分公式〉を示してみます（次節）。

チェーン法則

U, V, W はノルム空間で、f:U→V, g:V→W は連続写像とします。fは a∈V で最良線形近似 A を、gは b = f(a) ∈V で最良線形近似 B を持つとします。つまり：

  • f(a + u) = f(a) + Au + p(u) , p∈o(U, V)
  • g(b + v) = g(b) + Bv + q(v) , q∈o(V, W)

r(u) := Au + p(u) と置きます。A∈BL(U, V), BL(U, V) ⊆ Stbl(U, V) から A∈Stbl(U, V) 、p∈o(U, V), o(U, V) ⊆ Stbl(U, V) から p∈Stbl(U, V) 。Stbl(U V) はベクトル空間（足し算で閉じている）ので、r = A + p ∈Stbl(U, V) です。

b = f(a), v = r(u) を、g(b + v) = g(b) + Bv + q(v) に代入すれば：

  • g(f(a) + r(u)) = g(f(a)) + Br(u) + q(r(u))

[追記]ここから先何行かで、「p」と書くべきところが「r」になってました。修正しましたが、単に文字を置換しただけなので、消し線は使っていません。[/追記]

この等式の左辺は、g(f(a) + r(u)) = g(f(a) + Au + p(u)) = g(f(a + u)) = (g\circf)(a + u) 。右辺に出現する r(u) の一箇所を展開すると：

  • (g\circf)(a + u) = (g\circf)(a) + BAu + Bp(u) + q(r(u))

Bp(u) + q(r(u)) が o(U, W) に入ることが分かれば、この等式は g\circf の最良線形近似が BA であることを示します。

Bp(u) = (B\circp)(u), q(r(u)) = (q\circr)(u) なので、Bp(u) + q(r(u)) = (B\circp + q\circr)(u) 。B∈BL(V, W) ⊆ Stbl(V, W), p∈o(U, V) に、前節の結合に関する法則を適用して、B\circp∈o(U, W)。同様に、q\circr∈o(U, W) も言えるので、(B\circp + q\circr)∈o(U, W) です。

以上より、t := B\circp + q\circr とおいて、次のように書けます。

  • (g\circf)(a + u) = (g\circf)(a) + BAu + t(u), t∈o(U, W)

[追記]ここまで[/追記]

これで、g\circfの点aにおける最良線形近似が BA:U→W であることが確認できました。f'(a) = A, g'(b) = g'(f(a)) = B というよく使われる記法によれば：

  • (g\circf)'(a) = g'(f(a))f'(a)

お馴染みのチェーン法則です。

省略した証明

後回しにした証明をここでするのか、というと、しません。どんなことが後回しになっていたかだけ記しておきます。U, V, W はノルム空間です。

  1. UからVへの連続写像の空間 C(U, V) がベクトル空間になること。
  2. UからVへのスモールオーな関数の空間 o(U, V) がベクトル空間になること。
  3. UからVへの有界線形写像の空間 BL(U, V) がベクトル空間、そしてノルム空間になること。
  4. UからVへの安定な関数の空間 Stbl(U, V) がベクトル空間になること。
  5. BL(U, V) ⊆ C(U, V)
  6. C(U, V)∩L(U, V) = BL(U, V)
  7. p∈o(V, W), q∈o(V, W) ⇒ q\circp∈o(U, W)
  8. s∈Stbl(U, V), t∈Stbl(U, V) ⇒ t\circs∈Stbl(U, W)
  9. p∈o(V, W), t∈Stbl(U, V) ⇒ t\circp∈o(U, W)
  10. s∈Stbl(U, V), q∈o(V, W) ⇒ q\circs∈o(U, W)

登場した関数空間に慣れるのによい練習問題かと思います。

*1:「残余が残余であることを証明する」とか言うことになります。

*2:図式順結合記号';'を使うなら、o(U, V);o(V, W) ⊆ o(U, W) のように自然な形に書けます。