すべての随伴系達が作る構造は？ - 檜山正幸のキマイラ飼育記 (はてなBlog)

最近、二重圏に興味を持っています（「二重圏、縦横をもう一度」参照）。モナドや随伴には昔から興味を持っています。

すべての随伴系〈adjunction〉達を二重圏、あるいは2-二重圏に組織化することを考えたことがあります。

随伴系の二重圏 (2019年)
2-二重圏：随伴系達の圏 (2021年)

すべての随伴系達が作る構造について、またあらためて考えてみます。$`\newcommand{\mrm}[1]{ \mathrm{#1} }
\newcommand{\cat}[1]{ \mathcal{#1} }
\newcommand{\In}{\text{ in }}
\newcommand{\u}[1]{\underline{#1}}
\newcommand{\twoto}{ \Rightarrow }
%\newcommand{\hyp}{\text{－} }
%\newcommand{\NFProd}[3]{ \mathop{_{#1} \!\underset{#2}{\times}\,\!_{#3} } }
\newcommand{\dblcat}[1]{\mathbb{#1}}
\newcommand{\AdjI}[1]{ {_{#1}\!\mrm{Adj}} }
\newcommand{\AdjII}[2]{ {_{#1}\!\mrm{Adj}_{#2}} }
%\newcommand{\AdjIII}[3]{ {_{#1}\!\mrm{#2}\mrm{Adj}}^{#3} }
\newcommand{\AdjIV}[4]{ {_{#1}\!\mrm{#2}\mrm{Adj}}_{#3}^{#4} }
`$

内容：

参考資料と過去記事
動機と目的
随伴系の0-圏と1-圏
向き・名付け・書き方の約束
二重射、入れ替え2-射、右準同型射
左準同型射
メイトに関する条件
おわりに

参考資料と過去記事

二重圏は応用圏論〈Applied Category Theory〉の最近のトレンドです。他に、アクテゴリーやオプティックも盛り上がっているトピックです。去年〈2023年〉に登場した依存アクテゴリー（「依存アクテゴリーが面白い」参照）は、アクテゴリー／二重圏／三重圏／ファイブレーションなどを組み合わせた新しいフレームワークで、なかなか興味深いです。

依存型理論の圏論的モデルのなかに、依存アクテゴリーの実例があるかも知れないと期待しています。「依存型理論の圏論的セマンティクスの資料」に、参考になりそうな資料〈文献〉を列挙してます。後から追加した文献がコラリア／エメネガーの以下の論文です。今年〈2024年〉の3月5日にarXivに投稿された新しい論文です。

[CE24-]
Title: A 2-categorical analysis of context comprehension
Authors: Greta Coraglia, Jacopo Emmenegger
Submitted: 5 Mar 2024
Pages: 29p
URL: https://arxiv.org/abs/2403.03085

この論文の前半（10ページまで）では、コモナドと随伴系とのあいだの関係がレビューされています。2-圏内の随伴系を対象〈0-対象〉として、左射〈left morphism〉を射〈1-射〉とする2-圏が定義されています。この記事では、随伴系のあいだの右準同型射（コラリア／エメネガーの右射と同じモノ）を二重射〈四角形射〉に選んで、2-圏ではなくて二重圏／2-二重圏に組織化したいと思います。ただし、この記事では2-二重圏まで扱ってはいません。二重圏どまりです。

冒頭で挙げた2つの過去記事以外に、以下の記事でモナド達や随伴系達が構成する圏類似代数系〈category-like algebraic {system | structure}〉について述べています。

「最近のモナド論の概観と注意事項 1/2」で紹介した文献をひとつだけ再掲しておきます。バスケス-マルケスの次の論文です。

[Vaz15-17]
Title: Monad and Comonad Objects through 2-adjunctions of the type Adj-Mnd
Submitted: 15 Oct 2015 (v1), 8 Jun 2017 (v3)
Author: Adrian Vazquez-Marquez
Pages: 17p
URL: https://arxiv.org/abs/1510.04724

「最近のモナド論の概観と注意事項 2/2」からは、チェン／ガースキ／リエルの論文を再掲します。

[CGR12-]
Title: Multivariable adjunctions and mates
Authors: Eugenia Cheng, Nick Gurski, Emily Riehl
Submitted: 22 Aug 2012 (v1), 23 Aug 2012 (v2)
Pages: 52p
URL: https://arxiv.org/abs/1208.4520

動機と目的

依存アクテゴリーであれ型理論であれ、モナド／コモナドと随伴系は使います。応用のためには、モナド／コモナドと随伴系を、二重圏／三重圏ベースで組織化しておくのが都合が良さそうです。特に今回は、厳密2-圏内の随伴系達を2-二重圏に組織化することを考えます。

厳密2-圏 $`\cat{K}`$ 内のすべての随伴系〈adjunction | adjoint system〉達の集合を $`\AdjI{0}(\cat{K})`$ と書くことにします。先頭下付きの 0 は0-圏（つまり集合）であることを示しています。特に、$`\cat{K} = {\bf CAT}`$ であるときは次のように書きます。（$`\mathbb{SET}`$ と後で出てくる $`\mathbb{CAT}`$ については、「変換手n-圏のブラケット記法」の冒頭とそこからリンクされている過去記事を参照してください。）

$`\quad {_0\!{\bf Adj}} := \AdjI{0}( {\bf CAT} ) \in |\mathbb{SET}|`$

$`\AdjI{0}( \cat{K} )`$ を理解することは、個々の随伴系を理解することになります。$`\AdjI{0}(\cat{K})`$ では、2つの随伴系のあいだの関係性は考えません。

随伴系の方向を、随伴系の右1-射（圏達の2-圏内の随伴系なら右随伴関手）の方向と同じにして、随伴系を1-射とする1-圏を考えることができます。この1-圏は次のように書きます。

$`\quad \AdjII{1}{R}(\cat{K} ) \in |\mathbb{CAT}|`$

$`\AdjII{1}{R}`$ の $`R`$ は Right のことで、随伴系の方向を右1-射の方向にとることを示します。随伴系の方向を左1-射の方向にとるならば、$`\AdjII{1}{L}`$ です。特に、$`\cat{K} = {\bf CAT}`$ であるときは次のように書きます。

$`\quad {_1\!{\bf Adj}_R} := \AdjII{1}{R}( {\bf CAT} ) \In |\mathbb{CAT}|`$

$`{_1\!{\bf Adj}_R}`$ は通常の圏〈1-圏〉なので、その構造は比較的簡単です。が、2-圏、二重圏、2-二重圏として組織化するとなると話が複雑になります。その複雑な話を整理しておきたい、ということです。

随伴系の0-圏と1-圏

厳密2-圏を $`\cat{K}`$ として、 $`\cat{K}`$ 内の随伴系（集合 $`\AdjI{0}(\cat{K})`$ の要素）は、$`A, B`$ などラテン文字大文字で表します。その状況は次のように書けます。（以下の $`\mathbb{str}`$ は「厳密」を意味します。）

$`\text{For }\cat{K} \in |\mathbb{str2CAT}| \\
\quad \AdjI{0}(\cat{K}) \in |\mathbb{SET}| \\
\quad A, B \in \AdjI{0}(\cat{K})
`$

随伴系 $`A`$ を次のように書きます。

$`\quad A = (\u{A}_l, \u{A}_r, \eta^A, \varepsilon^A) \;\in \AdjI{0}(\cat{K})
`$

構成素は次のように呼びます。$`a := \mrm{dom}(\u{A}_l), b := \mrm{cod}(\u{A}_l)`$ と置きます。アスタリスク '$`*`$' は、厳密2-圏 $`\cat{K}`$ の横結合の図式順演算子記号です。

随伴系 $`A`$ の左1-射〈left 1-morphism〉： $`\u{A}_l : a \to b \In \cat{K}`$
随伴系 $`A`$ の右1-射〈right 1-morphism〉： $`\u{A}_r : b \to a \In \cat{K}`$
随伴系 $`A`$ の単位2-射〈unit 2-morphism〉：
$`\quad \eta^A :: \mrm{id}_a \twoto \u{A}_l * \u{A}_r : a\to a \In \cat{K}`$
随伴系 $`A`$ の余単位2-射〈counit 2-morphism〉：
$`\quad \varepsilon^A :: \u{A}_r * \u{A}_l \twoto \mrm{id}_b : b \to b \In \cat{K}`$

0-射〈対象〉、1-射の構成素は次のように描けます。

$`\quad \xymatrix@C+1pc{
a \ar@/^/[r]^{\u{A}_l} \ar@{}[r]|{\top}
& b \ar@/^/[l]^{\u{A}_r}
}\\
\quad \In \cat{K}
`$

随伴系の法則を与える等式（2つある）はニョロニョロ法則3-射〈snake law 3-morphism〉です。3-射とは、2-射のあいだの等式のことです。随伴系をストリング図とストリング図描き換えとして表すと次のようです。

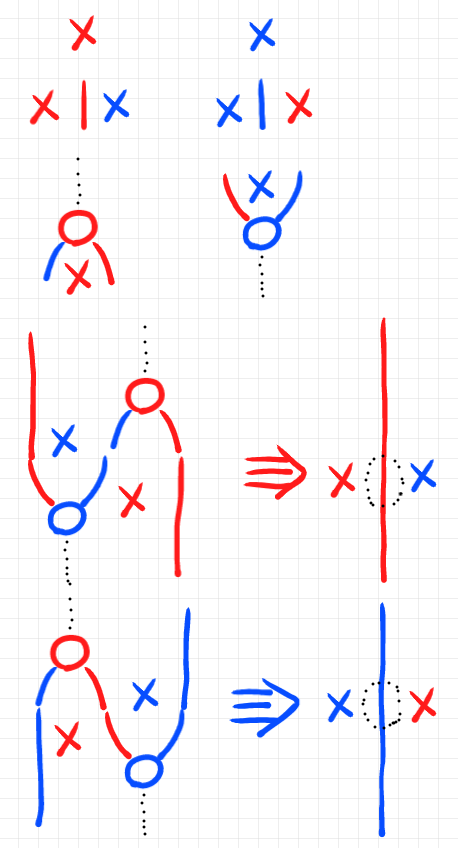
0-射は、バッテン（文字エックスではなくてエリア）
1-射は、ワイヤー
恒等1-射は、黒点線ワイヤー
2-射は、ノード
恒等2-射は、黒点線輪郭のノード
3-射は、ストリング図の描き換え〈変形〉

「アドホック随伴系と自由対象・台対象」に、ペースティング図と指標もあります。

随伴系 $`A`$ を圏 $`\AdjII{1}{L}( \cat{K} )`$ の1-射とみなしたものは次のように書きます。

$`\quad A_L = (\u{A}_l : a\to b, \u{A}_r, \eta^A, \varepsilon^A) \; : a \to b \In \AdjII{1}{L}( \cat{K} )`$

同様に、随伴系 $`A`$ を圏 $`\AdjII{1}{R}( \cat{K} )`$ の1-射とみなしたものは次のように書きます。

$`\quad A_R = (\u{A}_l, \u{A}_r : b\to a, \eta^A, \varepsilon^A) \; : b \to a \In \AdjII{1}{R}( \cat{K} )`$

定義から次が成立します。

$`\quad |\AdjII{1}{L}( \cat{K} )| = |\AdjII{1}{R}( \cat{K} )| = |\cat{K}| \In \mathbb{SET}\\
\quad \mrm{Mor}(\AdjII{1}{L}( \cat{K} )) = \mrm{Mor}(\AdjII{1}{R}( \cat{K} )) = \AdjI{0}( \cat{K} ) \In \mathbb{SET}\\
\quad (\AdjII{1}{L}( \cat{K} ) )^\mrm{op} = \AdjII{1}{R}( \cat{K} ) \In \mathbb{CAT}
`$

圏 $`\AdjII{1}{L}( \cat{K} )`$ における射の結合をテキストで書くと次のようになります。

$`\text{For }A_L = (\u{A}_l : a \to b, \u{A}_r, \eta^A, \varepsilon^A) : a \to b \In \AdjII{1}{L}( \cat{K} )\\
\text{For }B_L = (\u{B}_l : b \to c, \u{B}_r, \eta^B, \varepsilon^B) : b \to c \In \AdjII{1}{L}( \cat{K} )\\
\quad A_L * B_L := \\
\qquad (
\u{A}_l * \u{B}_l : a\to c,
\u{B}_r * \u{A}_r ,
\eta^A ; (\u{A}_l * \eta^B * \u{A}_r),
(\u{A}_r * \varepsilon^B * \u{A}_l ) ; \varepsilon^A
)\\
\qquad : a \to c \In \AdjII{1}{L}( \cat{K} )
`$

テキストで書くのは伝達のための必要悪なので、ストリング図を描いてみてください。

向き・名付け・書き方の約束

前節では、$`\cat{K}\in |\mathbb{str2CAT}|`$ に対して、1つの集合と2つの圏を定義しました。

$`\text{For }\cat{K} \in |\mathbb{str2CAT}| \\
\quad \AdjI{0}(\cat{K}) \in |\mathbb{SET}| \\
\quad \AdjII{1}{L}(\cat{K}) \in |\mathbb{CAT}| \\
\quad \AdjII{1}{R}(\cat{K}) \in |\mathbb{CAT}|\\
\text{Where}\\
\quad |\AdjII{1}{L}( \cat{K} )| = |\AdjII{1}{R}( \cat{K} )| = |\cat{K}| \In \mathbb{SET}\\
\quad \mrm{Mor}(\AdjII{1}{L}( \cat{K} )) = \mrm{Mor}(\AdjII{1}{R}( \cat{K} )) = \AdjI{0}( \cat{K} ) \In \mathbb{SET}\\
\quad (\AdjII{1}{L}( \cat{K} ) )^\mrm{op} = \AdjII{1}{R}( \cat{K} ) \In \mathbb{CAT}
`$

上記の0-圏、1-圏を含めて、ここで定義する圏類似代数構造〈category-like algebraic {system | structure}〉の一般的ネーミングルールは、次のテンプレートで表現できます。

$`\quad \AdjIV{\alpha}{\beta}{\gamma}{\delta, \epsilon}(\cat{K})`$

ここで、$`\alpha, \beta, \gamma, \delta, \epsilon`$ はプレースホルダーで、次のパラメータ値で埋めることになります。

$`\alpha \in \{\mrm{0}, \mrm{1}, \mrm{d}, \mrm{2d} \}`$
$`\beta \in \{ {\bf L} , {\bf R} \}`$
$`\gamma \in \{ L, R \}`$
$`\delta \in \{\mrm{pseu}, \mrm{str}\}`$
$`\epsilon \in \{\mrm{lax}, \mrm{pseu}, \mrm{str}\}`$

$`\alpha`$ は、構成される圏類似代数構造の種別です。

$`0`$ ： 0-圏、つまり集合
$`1`$ ： 1-圏、つまり通常の圏
$`d`$ ：二重圏〈double category〉
$`2d`$ ： 2-二重圏〈2-double category〉

$`\alpha`$ の選択によって、その他のパラメータの有無が変わってきます。$`\alpha = 0, 1`$ のときは既に述べましたが、ルールとしてまとめると：

$`\alpha = 0`$ のとき：残りのパラメータは無い。
$`\alpha = 1`$ のとき： $`\gamma`$ （説明はすぐ下）の指定が必要。その他のパラメータは無い。

$`\alpha = d, 2d`$ のときは、すべてのパラメータが必須になります。パラメータの意味は：

$`\beta`$ は、二重射として、左準同型射（$`{\bf L}`$）と右準同型射（$`{\bf R}`$）のどちらを採用するか。
$`\gamma`$ は、プロ1-射の向きを、随伴系の左1-射（$`L`$）と右1-射（$`R`$）のどちらに合わせるか。
$`\delta`$ は、二重射の入れ替え2-射（後述）として、可逆2-射（$`\mrm{pseu}`$ ＝ pseudo）と等式（$`\mrm{str}`$ ＝ strict）のどちらを採用するか。
$`\epsilon`$ は、二重射の入れ替え2-射のメイトに要求する条件として、無条件（$`\mrm{lax}`$）、可逆2-射（$`\mrm{pseu}`$）と等式（$`\mrm{str}`$）のどれを採用するか。

一例を挙げると、$`\AdjIV{d}{R}{L}{\mrm{str}, \mrm{pseu}}(\cat{K})`$ は次のような構造を表します。

二重圏である（$`\alpha = d`$）。
二重圏の二重射は、随伴系のあいだの右準同型射である（$`\beta = {\bf R}`$）。
二重圏のプロ1-射の方向は、随伴系の左1-射の方向である（$`\gamma = L`$）。
二重圏の二重射の入れ替え2-射は、$`\cat{K}`$ の等式〈3-射〉である（$`\delta = \mrm{str}`$）。
二重圏の二重射の入れ替え2-射のメイトは、$`\cat{K}`$ の可逆2-射である（$`\epsilon = \mrm{pseu}`$）。

$`\alpha = d, 2d`$ のとき、残りのパラメータは自由に選べるので、$`\beta, \gamma, \delta, \epsilon`$ の選び方は $`2\times 2\times 2\times 3 = 24`$ 種のバリエーションが現れます。構造が高次元になると、方向の選び方が爆発的に増えるので方向地獄〈direction hell〉と言っていいかも知れません*1。

方向地獄に対処するためのトレーニングについては：

双対や随伴に強くなるためのトレーニング

二重射、入れ替え2-射、右準同型射

2-圏の2次元の射（形状は円板）を2-射〈2-morphism〉と呼び、二重圏の2次元の射（形状は四角形）は二重射〈double morphism〉と呼びます。

$`\quad \xymatrix@C+1pc{
\cdot \ar@/^1.5pc/[r] \ar@/_1.5pc/[r] \ar@{}[r]|{\Downarrow}
& \cdot
}\\
\quad \In \cat{K}`$

$`\quad \xymatrix{
\cdot \ar@{-->}[r] \ar[d] \ar@{}[dr]|{\Downarrow}
& \cdot \ar[d]
\\
\cdot \ar@{-->}[r]
& \cdot
}\\
\quad \In \dblcat{D}`$

その形状から、2-射を円板{射}?〈disk {morphism}?〉*2、二重射を四角形{射}?〈square {morphism}?〉とも呼びます。ここで、「{‥‥}?」は省略可能を意味します。

厳密2-圏 $`\cat{K}`$ 内の随伴系の二重圏／2-二重圏でややこしいのは二重射〈四角形射〉です。二重射の種類として、（随伴系のあいだの）右準同型射と左準同型射があり、二重射の境界であるプロ1-射の方向も左と右の二種類があります。

まず、二重圏の射の種類と方向について、次の過去記事で確認しておいてください。

二重圏のプロ射〈プロ1-射〉の矢印には、なんらかの修飾を付けます。ここでは、プロ射に破線矢印を使っています。プロ射を縦方向に書けば二重射は次のようです。

$`\quad \xymatrix{
\cdot \ar@{-->}[d] \ar[r] \ar@{}[dr]|{\Rightarrow}
& \cdot \ar@{-->}[d]
\\
\cdot \ar[r]
& \cdot
}\\
\quad \In \dblcat{D}`$

「2-二重圏：随伴系達の圏」では、次のような描き方をしていました。波線矢印がプロ射です。

$`\quad \xymatrix{
\cdot \ar@{~>}[rr] \ar[d]
& {} \ar@{=>}[d]
& \cdot \ar[d]
\\
\cdot \ar@{~>}[rr]
& {}
& \cdot
}\\
\quad \In \dblcat{D}
`$

描画方向やプロ射矢印の修飾方法は色々ですが、描き方が違っても意図は同じなので柔軟に解釈してください。

事例として、$`\AdjIV{d}{R}{L}{\mrm{pseu}, \mrm{lax}}(\cat{K})`$ について述べます。右肩の $`{\mrm{pseu}, \mrm{lax}}`$ は「特に条件が無い」ことなので、単に $`\AdjIV{d}{R}{L}{}(\cat{K})`$ とも書きます。

$`A, A'`$ を $`\cat{K}`$ 内の随伴系（集合 $`\AdjI{0}(\cat{K})`$ の要素）として、次のような設定・略記をします。

$`a := \mrm{dom}(\u{A}_l) \In \cat{K}`$
$`b := \mrm{cod}(\u{A}_l) \In \cat{K}`$
$`a' := \mrm{dom}(\u{A'}_l) \In \cat{K}`$
$`b' := \mrm{cod}(\u{A'}_l) \In \cat{K}`$
$`r := \u{A}_r : b \to a \In \cat{K}`$
$`r' := \u{A'}_r : b' \to a' \In \cat{K}`$

$`\AdjIV{d}{R}{L}{}(\cat{K})`$ の二重射 $`\varphi`$ を考えます。「添加仮想二重圏 // 添加仮想二重圏の2-射のフレーム」で定義したテキスト記法でプロファイル（境界の仕様）を書けば次のようです。

$`\quad \varphi :: (f: a \to a')[A \twoto A'](g:b \to b') \In \AdjIV{d}{R}{L}{}(\cat{K})`$

次のように図示します。

$`\quad \xymatrix@C+1.5pc{
a \ar@{-->}[r]^{A} \ar[d]_f
\ar@{}[dr]|{\varphi\,\Downarrow\:}
& b \ar[d]^g \ar@/_1pc/[l]_{r}
\\
a' \ar@{-->}[r]_{A'}
& b' \ar@/^1pc/[l]^{r'}
}\\
\quad \In \AdjIV{d}{R}{L}{}(\cat{K})`$

ここで、実線矢印で描いている $`r, r'`$ は注釈情報で、二重圏のプロ1-射としての $`A, A'`$ の方向とは逆向きな $`r, r'`$ を考えることを示しています。

上記の二重射を厳密2-圏 $`\cat{K}`$ 内に展開すると、次の図式になります。

$`\quad \xymatrix{
b \ar[r]^r \ar[d]_g
& a \ar[d]^f \ar@{=>}[dl]|{\varphi}
\\
b' \ar[r]_{r'}
& a'
}\\
\quad \In \cat{K}`$

テキストで書くならば：

$`\quad \varphi :: r*f \twoto g*r' : b \to a' \In \cat{K}`$

上の図式を反時計回りに45度回転させると、次のレイアウトになります。

$`\quad \xymatrix{
{}
& a \ar[dr]^f \ar@{}[dd]|{\varphi\,\Downarrow\:}
& {}
\\
b \ar[ur]^{r} \ar[dr]_{g}
&{}
& a'
\\
{}
& b' \ar[ur]_{r'}
& {}
}\\
\quad \In \cat{K}`$

この形を、ストリング図で2本のワイヤーが交差するノードだとみなして、入れ替え2-射〈swapper 2-morphism〉と呼ぶことにします。入れ替え2-射をテキストで書くときは次の形にします。

$`\quad \varphi = \begin{pmatrix}
r & a & f \\
{} & \varphi \Downarrow & {}\\
g & b' & r'
\end{pmatrix} : b \to a' \In \cat{K}
`$

次のストリング図をテキストに写し取ったモノだと思ってください。

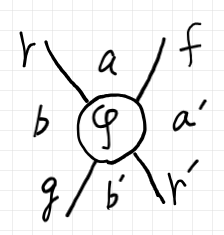
随伴系やモナドの計算では入れ替え2-射（ストリング図では4本脚の2-射ノード）がよく出てくるので、テキスト記法を決めておく価値はあるでしょう。

さて、入れ替え2-射 $`\varphi`$ を、“プロ射とみなした随伴系 $`A`$ から $`A'`$ への二重射”と考えるのですが、$`\varphi`$ の定義には、$`A, A'`$ の右1-射 $`r, r'`$ しか関与していません。なので、この形の二重射を、随伴系のあいだの右準同型射〈left homomorphism〉と呼びます。

随伴系のあいだの右準同型射では、単なる入れ替え2-射ではなくて、可逆性または厳密性の条件を課します。

入れ替え2-射 $`\varphi`$ が可逆な場合は、スード右準同型射〈pseudo right homomorphism〉と呼ぶ。
入れ替え2-射 $`\varphi`$ が等式（恒等2-射）な場合は、厳密右準同型射〈strict right homomorphism〉と呼ぶ。

コラリア／エメネガーの [CE24-] では、スード右準同型射をルーズ右射〈loos left morphism〉、厳密右準同型射を単に右射〈left morphism〉と呼んでいます。しかし、二重圏が出てくると、「ルーズ／タイト」は二重圏の1-射の種別と方向に使われるのでコンフリクトします。ここでは、「スード／厳密」にします。

ところで、右準同型射の入れ替え2-射のメイト（後述）に対する条件でもスード／厳密が出てきます。こちらは、メイト・スード／メイト厳密にします。例えば、「メイト厳密なスード右準同型射」といった具合です。

左準同型射

随伴系をプロ射とする二重圏の二重射としての左準同型射〈left homomorphism〉を考えましょう。このときも、プロ射の方向を左1-射の方向にとるか、右1-射の方向にとるかで別な二重圏ができます。

$`\AdjIV{d}{L}{L}{}(\cat{K})`$
$`\AdjIV{d}{L}{R}{}(\cat{K})`$

ここでは、$`\AdjIV{d}{L}{L}{}(\cat{K})`$ を考えます。随伴系の左1-射の方向がプロ射の方向で、関与する射も左1-射です。

前節と同様に、次のような設定・略記をします。

$`a := \mrm{dom}(\u{A}_l) \In \cat{K}`$
$`b := \mrm{cod}(\u{A}_l) \In \cat{K}`$
$`a' := \mrm{dom}(\u{A'}_l) \In \cat{K}`$
$`b' := \mrm{cod}(\u{A'}_l) \In \cat{K}`$
$`l := \u{A}_l : a \to b \In \cat{K}`$
$`l' := \u{A'}_l : a' \to b' \In \cat{K}`$

$`\AdjIV{d}{L}{L}{}(\cat{K})`$ の二重射 $`\psi`$ のプロファイルをテキスト記法で書けば次のようです。

$`\quad \psi :: (f: a \to a')[A \twoto A'](g:b \to b') \In \AdjIV{d}{L}{L}{}(\cat{K})`$

次のように図示します。

$`\quad \xymatrix@C+1.5pc{
a \ar@{-->}[r]^{A} \ar[d]_f \ar@/^1pc/[r]^{l}
\ar@{}[dr]|{\psi\,\Downarrow\:}
& b \ar[d]^g
\\
a' \ar@{-->}[r]_{A'} \ar@/_1pc/[r]_{l'}
& b'
}\\
\quad \In \AdjIV{d}{L}{L}{}(\cat{K})`$

今回は、プロ射の方向と、実際に関与する左1-射の方向が揃っています。

右準同型射である二重射 $`\psi`$ を厳密2-圏 $`\cat{K}`$ 内に展開すると、次の図式になります。

$`\quad \xymatrix{
a \ar[r]^l \ar[d]_f
& b \ar[d]^g
\\
a' \ar[r]_{l'} \ar@{=>}[ur]|{\psi}
& b'
}\\
\quad \In \cat{K}`$

テキストで書くならば：

$`\quad \psi :: f * l' \twoto l *g : a \to b' \In \cat{K}`$

上の図式を反時計回りに45度回転させると、次のレイアウトになります。

$`\quad \xymatrix{
{}
& b \ar[dr]^g \ar@{}[dd]|{\psi\,\Uparrow\:}
& {}
\\
a \ar[ur]^{l} \ar[dr]_{f}
&{}
& b'
\\
{}
& a' \ar[ur]_{l'}
& {}
}\\
\quad \In \cat{K}`$

行列風のテキストで書くときは次の形にします。

$`\quad \psi = \begin{pmatrix}
l & b & g \\
{} & \psi \Uparrow & {}\\
f & a' & l'
\end{pmatrix} : a \to b' \In \cat{K}
`$

テキスト記法で上下方向を逆向きにする（書き方を単に変える）と：

$`\quad \psi = \begin{pmatrix}
f & a' & l' \\
{} & \psi \Downarrow & {}\\
l & b & g
\end{pmatrix} : a \to b' \In \cat{K}
`$

この節の二重射の作り方は実はクインテット構成です（「2-圏からのクインテット構成で二重圏」参照）。

前節の二重射（の入れ替え2-射）と並べて書いてみると次のようです。

$`\quad \varphi = \begin{pmatrix}
r & a & f \\
{} & \varphi \Downarrow & {}\\
g & b' & r'
\end{pmatrix} : b \to a' \In \cat{K}\\
\:\\
\quad \psi = \begin{pmatrix}
f & a' & l' \\
{} & \psi \Downarrow & {}\\
l & b & g
\end{pmatrix} : a \to b' \In \cat{K}
`$

メイトに関する条件

メイトについては、「随伴系の二重圏 // メイト」に説明があります。

随伴系のあいだの左準同型射／右準同型射の入れ替え2-射は、（ストリング図に描くと）4本脚を持ち、メイト構成可能な2-射です。メイトの構成法に関しては、「随伴系の二重圏 // メイト対応」の絵を再掲しておきます。

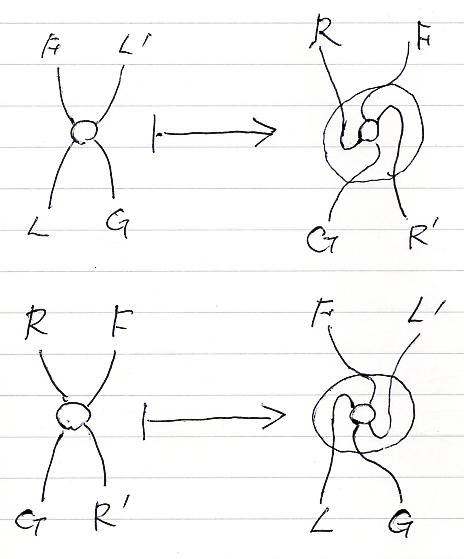
この絵では、$`L', L`$ が2つの随伴系の2つの左1-射、$`R, R'`$ が2つの随伴系の2つの右1-射です。メイトを作るには、随伴系の単位／余単位を繋ぎます。

随伴系の左準同型射／右準同型射において、入れ替え2-射のメイトに条件を付けることがあります。条件にしたがって、左準同型射／右準同型射を次のように呼ぶことにします。

メイトに条件を付けないなら、メイト・ラックス〈mate lax〉な左準同型射／右準同型射
メイトが可逆2-射である場合は、メイト・スード〈mate pseudo〉な左準同型射／右準同型射
メイトが等式〈恒等2-射〉である場合は、メイト厳密〈mate strict〉な左準同型射／右準同型射

おわりに

実際に説明した二重圏は $`\AdjIV{d}{R}{L}{}(\cat{K})`$ と $`\AdjIV{d}{L}{L}{}(\cat{K})`$ でしたが、残りのバリエーションの作り方も容易に想像が付くでしょう。

$`\AdjIV{d}{R}{L}{}(\cat{K})`$
$`\AdjIV{d}{R}{R}{}(\cat{K})`$
$`\AdjIV{d}{L}{L}{}(\cat{K})`$
$`\AdjIV{d}{L}{R}{}(\cat{K})`$

随伴系の左準同型射／右準同型射の実体である入れ替え2-射とそのメイトの条件を考えると、さらに再分類されます。

2021年の過去記事「2-二重圏：随伴系達の圏」では、タイト方向に垂直な第三の方向の2-射を追加してさらに次元を上げています。これについても再度整理したいですが、それは次の機会に。

*1:「依存アクテゴリーに向けて」で、「一貫性地獄〈coherece hell〉」という言葉を紹介しました。組み合わせ的爆発は地獄を招来します。

*2:「依存アクテゴリーが面白い」で紹介したように、「円板」はエドワード・モアハウス〈Edward Morehouse〉が使っていた用語法で、2次元の球体射〈globular morphism〉のことです。