カントールは間違っていた from viXra.org - 檜山正幸のキマイラ飼育記 (はてなBlog)

おうちでヴィクスラ〈viXra.org〉を読もう

こんな状況*1だと、なんか気分転換がしたくなります。「viXraを眺める」に書いたように、viXra（https://vixra.org/）論文には、癒しになるものがあります。

論文を選ぶときの僕の規準は：

短いもの。長いと読む気になれないので。
解釈可能なもの。何を言ってるか不明だと、解読の労力が辛いので。

念のために断っておくと（「viXraを眺める」からそのまま引用）：

viXra論文がみんなトンデモってわけではないです。まだ完成度が低いドラフト（だが、マトモなもの）を一時的に公開している人もいます。なかには、思い付きや勉強した内容をメモしておくのに使っている人もいるようです。PDFベースのgistみたいな感じで。
自分が書いたものにメタデータとURLが付いて、バージョン管理もしてくれるので、そういうサービスとして利用するのもアリかも知れませんね。

今回は次を選びました。

Title: Cantor Diagonal Argument is false
Author: Richard L. Hudson
Pages: 3p
URL: https://vixra.org/abs/2001.0024

「☓☓☓は間違っている／間違っていた」系の論文です。「☓☓☓」で圧倒的人気を誇るのは「アインシュタイン」です。この論文では、集合論の「カントール」がターゲットです。

著者のハドソン〈Richard L. Hudson〉さんは、対角線論法を使ったカントールの定理は間違っていると主張します。ハドソンさんの議論を紹介しましょう。

カントールの対角線論法

まずは、もとのカントールの定理から；

自然数の集合 N = {0, 1, 2, ...} から二元集合 {0, 1} への写像の全体を {0, 1}^N = Map(N, {0, 1}) とします。a∈{0, 1}^N に、集合 A := {n∈N | a(n) = 1} を対応させる1：1対応で、{0, 1}^N $\cong$ Pow(N) （Pow(N) はNのベキ集合）です。カントールの定理は次の命題です。

N $\cong$ {0, 1}^N ではない。

集合と写像の概念・記法、「ではない」を意味する論理記号「￢」、「存在する」を意味する論理記号「∃」、「かつ」を意味する論理記号「∧」を使って書くと：

￢( ∃ f:N→{0, 1}^N, g:{0, 1}^N→N.( g $\circ$ f = id_N ∧ f $\circ$ g = id_{{0, 1}^N} ) )

となります。( ∃… ) の部分を簡略に書くと N $\cong$ {0, 1}^N です。

カントールの定理は否定の形をしているので、背理法を使い、肯定の形から矛盾を出します。書き換えられた命題は：

N $\cong$ {0, 1}^N ⇒ ⊥

ここで、「⊥」は「矛盾」を表す記号です。矛盾は、A∧￢A という形の命題として現れます。

対角線論法の説明はWikipedia項目などを眺めてもらうことにして、説明図をハドソン論文からコピーすると：

図で下線が引いてある値を拾って並べると 110011… となり、これを対角列 d とします。1を0に、0を1に置き換えた列を、もとの列の補列〈complementary sequence〉とハドソンさんは呼んでいます。対角列 d の補列を p とします。

{0, 1}^N の列を並べた可算集合（と仮定する）は L とします。カントールによれば、対角列の補列 p は L に属さない。しかし、どんな列も L に属すると仮定したので、

p∈L ∧ ￢(p∈L)

となり矛盾が出ます。

ハドソンのツリー論法

いよいよハドソンさんの論法です。ハドソンさんは次のような無限バイナリツリー〈二進木 | 二分木〉を考えます。

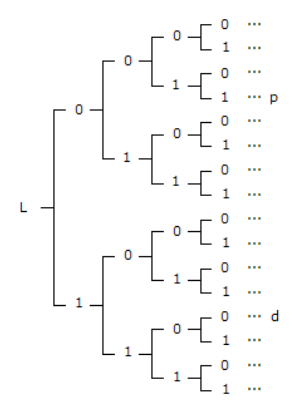
この無限ツリーを B と置きましょう。B を有向グラフと考えて、ルートから出る無限パスの全体を Path(B) とします。{0, 1}の列とパスとの対応から、Path(B) $\cong$ {0, 1}^N がいえます。いいですよね。注目すべきは、ハドソンさんの次の言明です。

The tree therefore is a representation of L as defined in par.1.
よって、このツリーは第1節で定義した集合 L の表現となる。

「集合 L の表現となる」とは、Path(B) $\cong$ L ということです。

Path(B) には（同じことだが、{0, 1}^N には）次の性質があります。

[対称性] x∈Path(B) ならば、(xの補列)∈Path(B) である。

この性質のハドソンさんの説明は実にビジュアルで：

先のツリーの図において、ルートを通る水平線〈横線〉を引いて、その線に対する鏡映〈線対称〉を考えればよい。例として、d とその補列 p を描いている。

さて、d が L の対角列だとします。d に対応するパスも同じく d と表すと、すぐ上の対称性から、 d の補列 p もまたパスであり、したがって L に所属します。カントールは、d の補列 p は L に所属しないと言っているが、実は所属する。カントールは間違っていた というわけです。

カントールの論法 vs ハドソンの論法

ハドソンさんの論法は、論点先取になるのかな？

カントールの主張は￢( N $\cong$ {0, 1}^N ) なので、これをしりぞけたいなら、その否定（二重否定の法則をOKとして）N $\cong$ {0, 1}^N を仮定すれば、カントールの定理は（当該の仮定から）間違っていると言えます。

僕の推測ですが、ハドソンさんは、無限バイナリツリー B と、そのパスの集合 Path(B) を混同はしてないまでも、なんか似たものだと思っていたのでしょう。B の絵を見ると可算っぽいです。だから、B のパスの集合も可算であり、L と（集合として）同型だと思ったのではないでしょうか（ま、推測ですがね）。

*1:この記事が過去記事になったときのための注釈：2020年4月、世界は新型コロナウィルス禍にみまわれています。