この記事は、後で書く予定の記事から参照されることを意図しています。2つの不動点なし対合に対して、ある種の結合(オペラッド結合と呼ぶのですが)を定義して、それが再び不動点なし対合になることを示します。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\cat}[1]{\mathcal{#1}}
%\newcommand{\twoto}{\Rightarrow }
\newcommand{\In}{\text{ in } }
%\newcommand{\Imp}{ \Rightarrow }
%\newcommand{\Iff}{\Leftrightarrow }
%\newcommand{\hyp}{\text{-} }
%\newcommand{\op}{\mathrm{op} }
\newcommand{\id}{\mathrm{id} }
%\newcommand{\B}{\partial } % boundary
%\newcommand{\mbf}[1]{\mathbf{#1}}
\newcommand{\pto}{ \supseteq\!\to }
\newcommand{\u}[1]{\underline{#1}}
\require{color} % 緑色
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }%
\newcommand{\For}{\Keyword{For } }%
\newcommand{\Define}{\Keyword{Define } }%
\newcommand{\Subject}{\Keyword{Subject } }%
\newcommand{\Where}{\Keyword{Where } }
%\newcommand{\Let}{\Keyword{Let } }
`$
内容:
状況設定
$`A, B, C`$ は有限集合で、互いに共通部分がないとします。
$`\quad A \cap B = \emptyset \\
\quad A \cap C = \emptyset \\
\quad B \cap C = \emptyset
`$
共通部分がない集号達の場合、直和を作っても合併しても同じ(集合として同型)なので、合併も $`A + B`$ のように書きます。
次のような2つの関数を考えます。
$`\quad f: A + B \to A + B \In{\bf Set} \\
\quad g: B + C \to B + C \In{\bf Set}
`$
記法の簡略化のために、
$`\quad AB := A + B\\
\quad BC := B + C
`$
と置きます。
$`f, g`$ は単なる自己写像〈endomorphic map〉ではなくて、不動点なし対合だとします。
$`\quad f;f = \id_{AB} \,\land\, \forall x\in AB.\, f(x)\ne x\\
\quad g;g = \id_{BC} \,\land\, \forall y\in BC.\, g(y)\ne y
`$
対合であることから $`f = f^{-1}, g = g^{-1}`$ は出ます。$`f, g`$ は可逆写像です。
ランド・オア・ホップ
ランド・オア・ホップ〈land or hop〉は、$`f: AB \to AB`$ と $`g: BC \to BC`$ から新しい関数 $`h`$ を作るときに使うアルゴリズムのこと(僕の造語)です。
前節の $`f, g`$ が不動点なし対合という仮定は、この節ではいったん忘れて、$`f, g`$ は単に写像だとします。その場合、新しく作られる関数 $`h`$ は部分関数(値が未定義であることを許す関数)かも知れません。そのことを次のように書きます。
$`\quad h: AC \pto AC\\
\Where AC = A + C
`$
ランド・オア・ホップのアルゴリズムを説明します。
$`x\in A`$ に対して、$`ABC = A + B + C`$ 内の点列〈要素列〉を作ります。
$`\quad x = x_0, x_1, \cdots, x_N`$
$`N`$ は1以上の自然数です。場合により、点列は無限に続くかも知れません。
$`\quad x = x_0, x_1, x_ 2, \cdots`$
点列を作る手順は:
- $`x_1 = f(x_0)`$ とする。
- $`x_1 \not\in B`$ (同じことだが $`x_1 \in A`$)ならば、$`N = 1`$ で終了。
- $`x_1 \in B`$ ならば、 $`x_2 = g(x_1)`$ とする。
- $`x_2 \not\in B`$ (同じことだが $`x_2 \in C`$)ならば、$`N = 2`$ で終了。
- $`x_2 \in B`$ ならば、 $`x_3 = f(x_2)`$ とする。
- 以下同様。$`x_i`$ の $`i`$ と $`N`$ の値は変わるが、手順2から繰り返し。
関数 $`\tilde{f} : A \to AC`$ は次のように定義します。
- $`x\in A`$ に対して、上記のランド・オア・ホップのアルゴリズムが $`N`$ ステップで終了したときは、 $`\tilde{f}(x) = x_N`$ 。
- そうでないとき(無限に続くとき)は、 $`\tilde{f} = \bot`$ (未定義)。
$`\tilde{g} : C \to AC`$ も同様に定義します。
問題の新しい部分関数 $`h`$ は、
$`\quad h := [\tilde{f}, \tilde{g}] : AC \pto AC`$
ここで、$`[\tilde{f}, \tilde{g}]`$ は部分関数のコペアです。具体的には:
$`[\tilde{f}, \tilde{g}](t) := \\
\quad \text{if }t\in A \text{ then } \tilde{f}(t)\\
\quad \text{if }t\in C \text{ then } \tilde{g}(t)
`$
次の例では、$`h`$ は完全に未定義な関数になります。
$`\quad A := \{a\}\\
\quad B := \{b\}\\
\quad C := \{c\}\\
\quad f := (a \mapsto b, b\mapsto b)\\
\quad g := (c \mapsto b, b\mapsto b)
`$
ランド・オア・ホップで全域関数
この節では、当初の設定「$`f, g`$ は不動点なし対合」を復活させます。この条件(の一部)があるとき、ランド・オア・ホップのアルゴリズムで定義される関数 $`h`$ が全域関数、つまり未定義なところがない普通の関数になることを示します。
$`\tilde{f}: A \to AC`$ が全域関数になることを示しましょう。もし、全域でないとするなら、とある $`x\in A`$ に対して次のようなランド・オア・ホップの無限点列が存在します。
$`\quad x = x_0, x_1, x_2, \cdots`$
ランド・オア・ホップのアルゴリズムから、$`x_1, x_2, \cdots`$ は集合 $`B`$ 内の無限点列です。$`B`$ は有限集合なので、無限点列は循環します。$`f`$ も $`g`$ も不動点を持たないので、循環点列は、長さ2以上のサイクルとなります。そのようなサイクルは2種類考えられます。
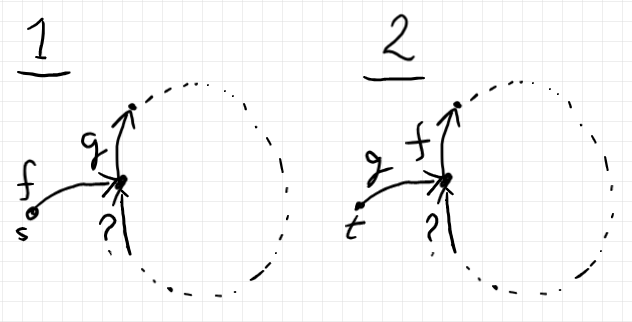
場合1のとき、$`s`$ は当該サイクルに含まれない点で、$`f`$ によりサイクルに突入してグルグル回ります。疑問符の写像は $`f`$ か $`g`$ のどちらかです。$`g`$ だとすると、ランド・オア・ホップのアルゴリズムに反します($`g`$ の後に $`g`$ はあり得ない*1)。したがって、疑問符の写像は $`f`$ です。もしそうだとすると、異なるニ点の値が $`f(s)`$ となります。これは、$`f`$ が単射であることに反します。場合1のサイクルは存在しません。
場合2のサイクルも、ランド・オア・ホップのアルゴリズムと $`g`$ が単射であることから存在できません。
同様にして、$`\tilde{g}: C \to AC`$ が全域関数になることも示せます。$`h = [\tilde{f}, \tilde{g}]`$ だったので $`h`$ も全域関数です。
ランド・オア・ホップの点列が $`x = x_0, x_1, \cdots x_N`$ のとき、$`x`$ から出発して、$`x_N`$ にランドした〈着地した〉ということにします。中間で通った点 $`x_1, \cdots, x_{N - 1}`$ ではホップしたということにします。今の前提では、まったくホップしないでランドするか、有限回ホップしてからランドするのどちらかしか起きなくて、無限にホップし続けることはできないことが分かりました。
実はホップし続けることもある
ランド・オア・ホップのアルゴリズムでは、集合 $`B`$ 内にランドすることはできません。集合 $`B`$ に入ったら必ずホップして次の場所に移動します。前節で無限にホップし続けることはできないと言いました。
確かに、集合 $`A`$ または $`C`$ から出発した場合は無限のホップはできません。が、集合 $`B`$ 内から出発して無限にホップし続けることはあります。次の例を考えましょう。
$`\quad A := \{a1, a2\}\\
\quad B := \{b1, b2\}\\
\quad C := \{c1, c2\}\\
\quad f := (a1 \mapsto a2, a2\mapsto a1, b1\mapsto b2, b2\mapsto b1)\\
\quad g := (c1 \mapsto c2, c2\mapsto c1, b1\mapsto b2, b2\mapsto b1)
`$
$`f`$ も $`g`$ も不動点を持たない対合です。$`B`$ 上では $`f`$ と $`g`$ が一致します。
この例で、$`b1`$ から $`f`$ で($`g`$ でも同じ)出発すると、次の無限点列が生じます。
$`\quad b1, b2, b1, b2, \cdots`$
このサイクルは $`B`$ 内で生じてますが、$`A, C`$ からこのサイクルに到達不可能なので、ランド・オア・ホップのアルゴリズムにおいては、このサイクルは無視されます。
目的によっては、$`B`$ 内で生じたサイクルを無視できないことがある、と注意しておきます。
不動点なし対合と同値関係
集合 $`X`$ 上に対合 $`k: X \to X`$ があると、$`x \in X`$ と $`k(x) \in X`$ を同値とみなす同値関係を定義できます。その同値類は二元集合か単元集合です。対合 $`k`$ が不動点を持たないなら、すべての同値類が二元集合になります。つまり、次の2つの概念は同じことです。
- 集合 $`X`$ 上の、不動点を持たない対合
- 集合 $`X`$ 上の、すべての同値類が二元集合である同値関係
2つの不動点を持たない対合 $`f, g`$ からランド・オア・ホップのアルゴリズムで作った $`h`$ が再び不動点を持たない対合であることを示すには、$`h`$ が定義する同値関係の同値類が二元集合であることを示せばOKです。
$`t \mapsto h(t)`$ をランド・オア・ホップで定義するとき、何回ホップしているかにより、$`t\mapsto h(t)`$ のホップ数を定義します。ホップ数は、アルゴリズムありきで決まる自然数で、写像や要素だけで決まるものではありません。
自然数 $`i`$ に対して、$`A, C`$ の部分集合 $`A_i, C_i`$ を次のように定義します。
$`\quad A_i = \{x \in A \mid x\mapsto h(x) \text{ のホップ数が} i \} \\
\quad C_i = \{z \in C \mid z\mapsto h(z) \text{ のホップ数が} i \}
`$
これらの部分集合を列挙するとき、次のレイアウトで配置すると便利です。
$`\quad \begin{matrix}
A_0 & C_0 \\
A_1 & C_1 \\
A_2 & C_2 \\
\vdots & \vdots\\
A_n & C_n
\end{matrix}`$
ここで、$`n`$ は十分に大きな自然数で、次が成立するとします。
$`\quad A = \sum_{i = 0}^n A_i\\
\quad C = \sum_{i = 0}^n C_i
`$
それぞれの部分集合において $`h`$ がどのような写像で定義されるかを同じレイアウトで列挙すると次のようです。
$`\quad \begin{matrix}
f & g \\
f;g & g;f \\
f;g;f & g;f;g \\
\vdots & \vdots\\
f;\cdots;f & g;\cdots ; g
\end{matrix}`$
これらを眺めると次のことが分かります。
- $`A_0`$ 上に $`x \sim f(x)`$ として同値関係 $`\sim`$ が入る。
- $`C_0`$ 上に $`z \sim g(z)`$ として同値関係 $`\sim`$ が入る。
- $`A_1 + C_1`$ 上に $`x \sim g(f(x))`$ (同じことだが $`z \sim f(g(z))`$)として同値関係 $`\sim`$ が入る。
- $`A_2`$ 上に $`x \sim f(g(f(x) ))`$ として同値関係 $`\sim`$ が入る。
- $`C_2`$ 上に $`z \sim g(f(g(z) ))`$ として同値関係 $`\sim`$ が入る。
- 以下、同様。
各部分集合上に入る同値関係では、同値類が二元集合になっています。よって、部分集合達を寄せ集めた全体に入る同値関係も同値類が二元集合になります。
おわりに
この記事では、素朴に組み合わせ的な議論をしました。実際には絵図的〈pictorial | graphical | diagrammatic〉な意味があり、絵を描いたほうが直感的です。絵図的解釈はまたいずれ。
*1:たまたま、$`f`$ と $`g`$ の値が等しいことは起こり得ます。