ストリング図のテキスト化：ボックス＆ポート方式 - 檜山正幸のキマイラ飼育記 (はてなBlog)

[ストリング図のテキスト化は]大変なんです。大変でやる気になれないのですが、でもやらざるを得ないでしょう -- 低コストの情報伝達手段がテキスト化する以外にないので。

という事情で、テキスト化の方法をハッキリさせていくことにします。

目の前にあるストリング図をテキストとして書き下すには次の作業が必要です。

ストリング図のすべての構成素に名前（番号も含む）を付ける。
構成素のあいだの繋がり具合を何らかの形で書き出す。

ストリング図の構成素は「ノードとワイヤー」と考えるのが普通ですが、ここでは別な見方を紹介します。ストリング図の構成素は「ボックスとポート」だと考えます。ストリング図を、ボックス＆ポートの集まりと考えると、繋がり具合の記述が少し楽になります。$`%
\require{color}
\newcommand{\di}[1]{\textcolor{orange}{#1} } % dummy index % 使う
%`$

内容：

同値なグラフ
セマンティックラベルと識別ラベル
ノード＆ワイヤー方式
ボックスとポート
ボックス＆ポート方式
[追記] ETBダイアグラム

関連記事群のハブ記事：ストリング図と相性が良いテンソル計算 1/2

同値なグラフ

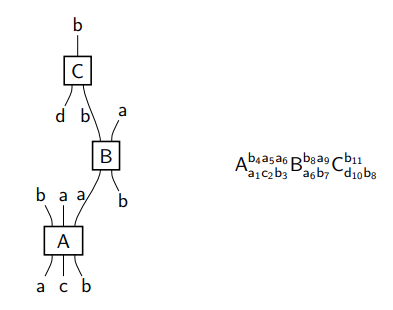
次の図は、スピヴァック〈David I. Spivak〉のスライド Wiring diagrams and state machines にあった絵の一部を抜き出して、構成素（ノードとワイヤー*1）に僕が名前（赤字）を付けたものです。

以下の2つのグラフ〈有向グラフ〉は、上記のストリング図と同じ情報を持つグラフです。

この記事では、二番目のグラフの方式を経由してテキスト化する方法を紹介します。

セマンティックラベルと識別ラベル

本論に入る前に大事な注意事項を述べます。ストリング図のラベルの話です、ラベルに関する無理解・誤解が多いので。

以下は以前の記事で出したアーディ〈Lucien Hardy〉による絵図とテキストの対応です。

ノード／ワイヤーが、大文字の A, B, C と小文字の a, b, c, d でラベルされています。テキストに出現する 1 から 11 の番号もワイヤーのラベルです（この絵には番号が書いてありませんが）。英字〈ラテン文字〉のラベルと番号のラベルでは目的が異なります。英字のラベルは意味的な情報を提供しますが、番号のラベルはワイヤーを識別するだけです。

意味的な情報を提供するラベルをセマンティックラベル〈semantic label〉、識別用のラベルは識別ラベル〈identification label〉と呼び区別することにします。

セマンティックラベルは、ワイヤーやノードが何を意味するかを示します。解釈の環境が集合圏なら、ワイヤーには集合の名前がラベルされ、ノードには写像の名前がラベルされます。解釈の環境がテンソルの圏なら、ワイヤーには自然数（または有限集合の名前）がラベルされ、ノードにはテンソルの名前がラベルされます。異なるワイヤーが同じ対象、異なるノードが同じ射を表すことはあるので、同一のラベルが異なる場所で何度も使われても問題にはなりません。

一方で、識別ラベルはワイヤー／ノードを識別するもので、意味とは関係ありません。同じラベルを違うワイヤー／ノードに付けることは出来ません。ワイヤー用ラベルとノード用ラベルを別な名前空間〈記号空間〉とすれば、同じ名前を使えますが、その場合の「同じ」はローカル名が同じだけで、完全修飾名〈fully qualified name〉は違います。完全修飾名で考えれば、やはり「同じ名前は使えない」のです。異なるワイヤー／ノードには異なる名前を付ける必要があります。

セマンティックラベルと識別ラベルを混同すると話がワヤクチャになるのでキチンと区別してください。我々が普通に見るラベルはセマンティックラベルです。テキスト化するときに識別ラベルが必要になります。たまたまセマンティックラベルによりワイヤー／ノードを識別できるときは、セマンティックラベルを識別ラベルに流用するときがあります。これはあくまで「たまたま」「流用」であって、役割としてのセマンティックラベルと識別ラベルは別物です。

ノード＆ワイヤー方式

この記事の主題は、識別ラベリング方式としての“ボックス＆ポート方式”ですが、よく知られている“ノード＆ワイヤー方式”を復習しておきましょう。

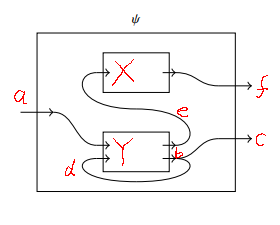
ノード＆ワイヤー方式は、ノードとワイヤーに識別ラベルを付けます。セマンティックラベルと区別するために番号を使います。ノード識別ラベルは n1, n2, ... 、ワイヤー識別ラベルは w1, w2, ... という通し番号にします。冒頭に挙げたストリング図を例題として再掲します。

ラベルを次のようにリネーム、または新たにネーミングします。

X → n1 （穴だが、ノード扱いしてもいい）
Y → n2 （穴だが、ノード扱いしてもいい）
分岐ノード → n3
a → w1
b → w2
c → w3
d → w4
e → w5
f → w6

味も素っ気もないですが、識別ラベルはセマンティックラベルではないので味も素っ気もなくてよいのです。

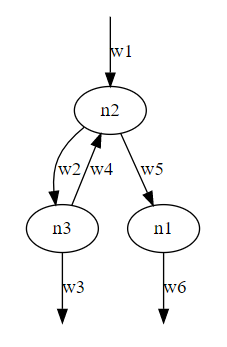
上記の識別ラベルと、ノードとワイヤーの繋がり具合を指定して、グラフ描画ソフトウェア Graphviz で有向グラフを描いてみます。それが下図です（これも再掲）。

2つの絵は、印象が違いますが、問題は印象ではなくて構造です。構造の記述としてグラフの接続行列〈incidence matrix〉を書いてみます。ワイヤーは有向辺なので、根本にマイナス符号、先端にはプラス符号を与えます。接続行列は次のように作ります；ノードと有向辺の根本／先端が接続していれば 1 を、そうでなければ 0 を行列成分にします。

$`\begin{array}{c|ccc}
&n1 &n2 &n3 \\
\hline
w1-& 0 & 0 & 0 \\
w1+& 0 & 1 & 0 \\
w2-& 0 & 1 & 0 \\
w2+& 0 & 0 & 1 \\
w3-& 0 & 0 & 1 \\
w3+& 0 & 0 & 0 \\
w4-& 0 & 0 & 1 \\
w4+& 0 & 1 & 0 \\
w5-& 0 & 1 & 0 \\
w5+& 1 & 0 & 0 \\
w6-& 1 & 0 & 0 \\
w6+& 0 & 0 & 0
\end{array}
%`$

ワイヤー w1 の根本 w1- はどのノードとも接続していません。ストリング図では開放辺〈オープンエッジ | ハーフエッジ | ルーズエッジ | フラグ | ダート〉を認めるのでこのような事が起こります。

上記の接続行列は絵を見ながら作りましたが、古典テンソル計算風のテキスト化（すぐ下）からでも、同じ接続行列は得られるはずです。テキストから接続行列への変換アルゴリズムを考えてみてください。

$`\quad n1_{\di{w5}}^{w6}\, n2_{w1\, \di{w4}}^{\di{w5}\, \di{w2}}\, n3_{\di{w2}}^{\di{w4}\, w3}`$

添字の色は余計な情報ですし、ノードの番号は出現位置で代用できるので、実は次のテキスト表現でもかまいません。

$`\quad {_{w5}^{w6}},\, {_{w1\, w4}^{w5\, w2}},\, {_{w2}^{w4\, w3}}`$

上下添字である必要もないし、接頭辞の w も不要です。本質的な情報は、以下の入れ子のリストで表現できます。

$`\quad ( (5), (6) ),\, ( (1, 4), (5, 2) ),\, ( (2), (4, 3))`$

ボックスとポート

次の論文から絵を拝借します。

Title: String diagrams for traced and compact categories are oriented 1-cobordisms
Authors: David I. Spivak, Patrick Schultz, Dylan Rupel
Submitted: 5 Aug 2015 (v1), 19 Sep 2016 (v3)
Pages: 53p
URL: https://arxiv.org/abs/1508.01069

以下の図はワイヤリング図です。ワイヤリング図は穴のあいたキャンバスに描いたストリング図で、キャンバスに描けるノードの種類を制限したものです。点線の四角はキャンバスの輪郭で、内部の四角は穴です。曲がったワイヤーが何であるかは、ワイヤリング図を解釈する環境となる圏により異なります。コンパクト閉圏なら曲がりに対応する射が存在します。トレース付きモノイド圏なら曲がりは仮想スパイダーです。

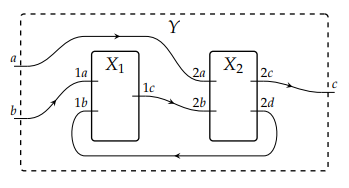
この図のラベルをよく見てください。ワイヤーにはラベルが付いてません。ワイヤーが四角形（キャンバス境界と穴の境界）を通過する場所にラベルが付いています。

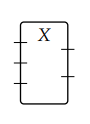
スピヴァック達は、キャンバス境界や穴の境界のような四角形をボックス〈box〉と呼んでいます。ボックスには、ワイヤーの通過点もマークされます。ワイヤーの通過点をポート〈port〉と呼びます。先のストリング図（ワイヤリング図）では、ポートにラベルが付いていたのです。ポート付きボックスを取り出すと次のようです（上の絵の一部を取り出したわけではなくて一般的事例として）。

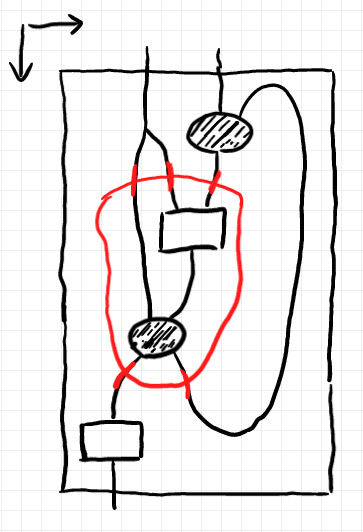
ボックスは、キャンバス境界や穴の境界よりもっと一般的な概念として捉えることができます。2次元キャンバス内の領域の境界をボックスと考えます。例えば、次の図の赤線の枠はボックスです。ボックスに付いているポートも赤で描いています。

すぐ上の図のボックスは四角くないですが、形が四角かどうかは問題ではありません。次の図では、ボックスに相当する枠は円で描かれています。

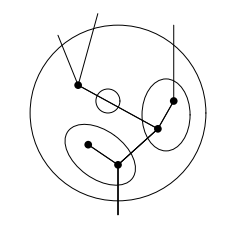
この図は次の論文からコピーしました。

Submitted: 7 Jun 2007 (v1), 21 Feb 2010 (v2)
Title: Polynomial functors and opetopes
Authors: Joachim Kock, André Joyal, Michael Batanin, Jean-François Mascari
Pages: 54p
URL: https://arxiv.org/abs/0706.1033

上記論文内では、ボックスに相当する概念をサークル〈円 | circle〉または球〈sphere〉と呼んでいます。もう一度言いますが、四角いか丸いかはどうでもいいハナシです。ボックスとサークルは同じ概念です*3。

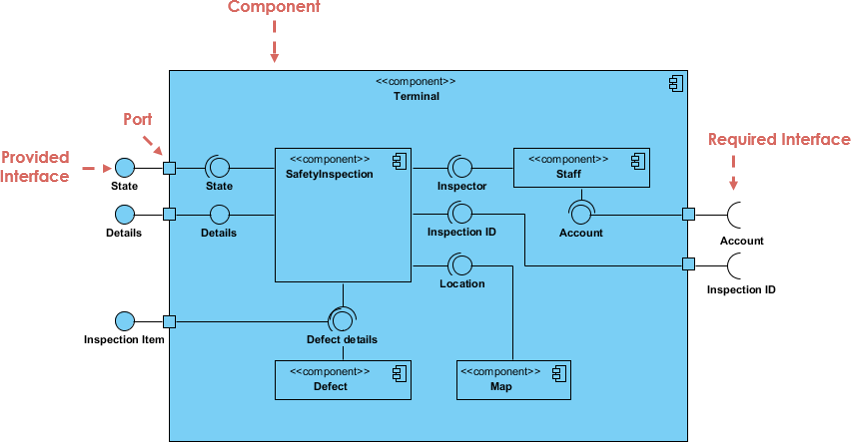
ちなみに、「ポート」という言葉は、スピヴァック達もコック達も使っていません。ソフトウェアコンポネントの図示の際に使われている言葉です。例えば、UML2のコンポネント図で「ポート」が使われています。

ボックス＆ポート方式

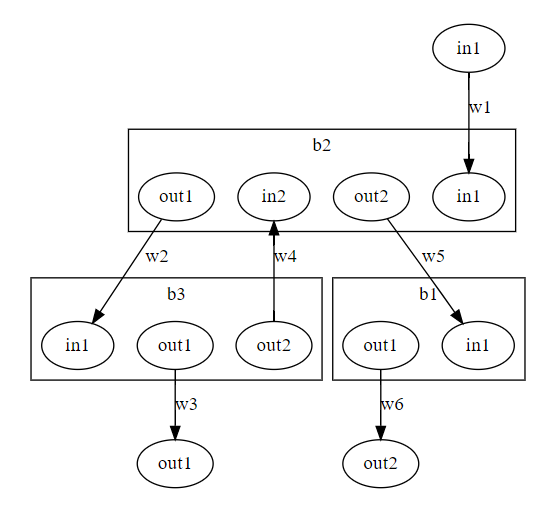
例題のストリング図をもう一度挙げます。

この図をボックスとポートの集まりとみなしてネーミングをやり直します。

キャンバスのボックス → b0
X のボックス → b1
Y のボックス → b2
分岐部分のボックス → b3
ボックス b0 のポート
1. 入力ポート： b0.in1
2. 出力ポート： b0.out1, b0.out2
ボックス b1 のポート
1. 入力ポート： b1.in1
2. 出力ポート： b1.out1
ボックス b2 のポート
1. 入力ポート： b2.in1, b2.in2
2. 出力ポート： b2.out1, b2.out2
ボックス b3 のポート
1. 入力ポート： b3.in1
2. 出力ポート： b3.out1, b3.out2

ボックスとポートだけに注目して描画すると次のようになります。

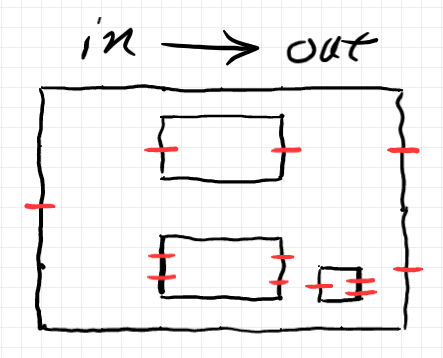
ポートはすべてで12個あります。ストリング図の繋がり具合は、ポートを頂点とする有向グラフで表現できます。その状況を Graphviz で描くと次のようです。外側のボックス b0 は描いてません。

12個の頂点（ポート）を繋ぐ有向辺達をデータとして記述するならば、隣接行列〈adjacency matrix〉が使えます。隣接行列はサイズが12×12の行列になりますが、これは疎行列（0が多い行列）です。0でない成分のインデックス（ポート識別ラベルのペア）を集合にすればいいでしょう。すると：

$`\quad \{
(\text{b0.in1}, \text{b2.in2}), (\text{b2.out1}, \text{b3.in1}), (\text{b3.out1}, \text{b0.out1}), \\
\quad (\text{b3.out2}, \text{b2.in2}), (\text{b2.out2}, \text{b1.in1}), (\text{b1,out1}, \text{b0.out2})
\}`$

この集合が繋がり具合を記述します。

ボックス＆ポート方式だと、キャンバスもポートを持つので、ワイヤーは（オープンエッジではなくて）通常の有向辺として記述できます。場合によっては、ノード＆ワイヤー方式より便利です。

いずれにしても、テキスト化の第一歩は識別ラベルを系統的に付けていくことなので、目的に応じてノード＆ワイヤー方式もボックス＆ポート方式も使えるようにしましょう。

[追記] ETBダイアグラム

僕が2004年12月に書いた記事（ブログ記事ではない）「ETBダイアグラム」があります。その当時、ソフトウェアに関する絵図としては、「ストリング図」という名称は一般的ではありませんでした。次のように書いています。

ある日、回路図とLEGOから、「電子ブロック」を連想した。そうだ、「電子ブロック・ダイアグラム」ならピッタリかもしれない。これが、「ETBダイアグラム」と呼びたい理由だが、別にこの呼称を普及させたいと思っているわけではい。“あのての図”を、それらしい呼び名で呼びたかっただけです。なにか一般的な呼称が定着すれば、それに従います。

ETBは"Electronics Toy Blocks"（電子ブロック）からです。「一般的な呼称」は「ストリング図」だったわけです。

当時のソフトウェア界隈で「ストリング図、ノード、ワイヤー」は一般的ではなかった（僕も使ってなかった）のですが、「ボックス、ポート」は使っていました。次のような絵を説明に使っています。