僕はストリング図が大好きです。ストリング図の利用・応用の範囲は広がっているようです。しかしながら現状においては、ストリング図の作成・公開・交換は容易ではないので、テキストに翻訳してコミュニケーションに使用することになります。テキスト化が好ましい手段でないのは重々承知ですが、現実的には致し方ありません。
ストリング図利用者は、ストリング図のテキストへのエンコード、テキストからストリング図へのデコードに習熟する必要があります。将来的には、ストリング図を直接使ってコミュニケーションが出来るようになると期待はしてます(「「コミュニケーションの多次元化」という革命に立ち会っているのだと思う」参照)が、現時点(21世紀初頭)ではテキスト・エンコード/デコードは(残念ながら)必須スキルです。$`%
\require{color}
\newcommand{\di}[1]{\textcolor{orange}{#1} } % dummy index % 使う
%`$
内容:
- 関連記事群のハブ記事: ストリング図と相性が良いテンソル計算 1/2
ワイヤーに識別子を付けて添字を使う
アーディ〈Lucien Hardy〉*1の論文(https://arxiv.org/pdf/1201.4390.pdf)から、彼が採用している記法を紹介します。
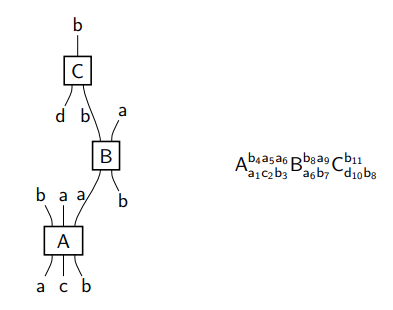
念のため、この図に関して説明しておきます。
- 描画方向は下から上、左から右です。僕〈檜山〉の習慣とは上下が逆です。
- 四角いノードは圏の射を表します。集合圏なら写像、関係圏なら関係、テンソルの圏ならテンソルです。ノードのラベルは大文字で、それは射の名前です。
- ワイヤーは圏の対象を表します*2。集合圏なら集合、関係圏でも集合、テンソルの圏なら自然数または有限集合です。ワイヤーのラベルは小文字で、それは対象の名前です。ワイヤーのラベルは、型〈タイプ〉、ソート、色〈カラー〉などとも呼ばれます。
左のストリング図は右のようにテキスト表現されます。テキスト表現の方法は:
- ノードのラベルを親文字とする。
- 親文字(大文字)の下付き添字として、射の域〈入力〉側情報、上付き添字として、射の余域〈出力〉側情報を書く。
- 添字の親文字(小文字)はワイヤーのラベル〈型 | ソート | 色〉とする。
- 添字の下付き添字(自然数値)として、ワイヤーの一意識別番号〈ID番号〉を付ける。
アーディの絵には一意識別番号が書いてありませんが、次のように、左から右/下から上に向かって 1 から 11 までの番号をふっています。
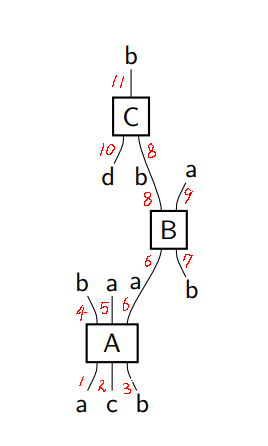
見れば分かるとは思いますが、老婆心からテキスト化の手順を書き下しておきます。
手順1: ワイヤーに番号〈ID〉を付ける。
手順2: 射(ノード)のプロファイルを読み取る。
- $`A:(a, c, b) \to (b, a, a)`$
- $`B:(a, b) \to (b, a)`$
- $`C:(d, b) \to (b)`$
手順3: プロファイルを上下の添字を使って書く。
- $`A_{a\, c\, b}^{b\, a\, a}`$
- $`B_{a\, b}^{b\, a}`$
- $`C_{d\, b}^{b}`$
手順4: 添字〈型 | ソート | 色〉の下付き添字としてワイヤー番号を書く。
- $`A_{a_1 c_2 b_3}^{b_4 a_5 a_6}`$
- $`B_{a_6 b_7}^{b_8 a_9}`$
- $`C_{d_{10} b_{8}}^{b_{11}}`$
手順5: 横に並べる。
$`\quad
A_{a_1 c_2 b_3}^{b_4 a_5 a_6} B_{a_6 b_7}^{b_8 a_9}
C_{d_{10} b_{8}}^{b_{11}}`$
クック〈Bob Coecke〉も、教材 http://www.cs.ox.ac.uk/ss2014/programme/Bob.pdf においてアーディと似た方法を採用しています。
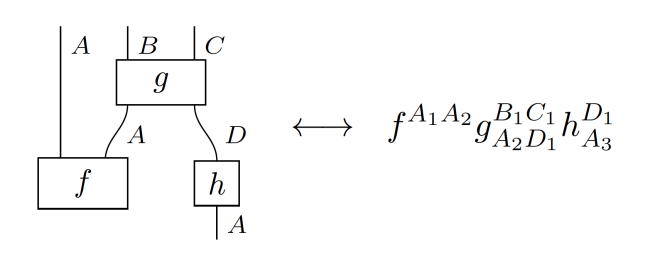
クックの場合は、ワイヤーに通し番号を付けるのではなくて、同じ型〈ソート | 色〉のワイヤーを区別する番号を付けます。上記の例では、型が $`B, C, D`$ のワイヤーは1本しかないので番号不要ですが、それでも番号 1 を付けています。
記述をより簡略化するために、ワイヤーに番号ではなくて名前〈識別子〉を付けます。次の規則に従いましょう。
- 型〈ソート | 色〉の名前(ラベル)が大文字なので、対応する小文字を添字にして、番号の代わりにダッシュ〈プライム〉を付けて区別する。
この規則でテキスト化すると:
$`\quad f^{a\, a'}\,g_{a'\, d}^{b\, c}\,h_{a''}^{d}`$
古典テンソル計算(「ストリング図と相性が良いテンソル計算 1/2 // 古典テンソル計算」参照)では、このような規則が使われることがあります。ただし、ダッシュで識別するよりは、特定の型〈ソート | 色〉に所属する添字用文字を前もって約束して使うことが多いです。明示的約束ならいいのですが、たいていは暗黙の約束です。
「ストリング図と相性が良いテンソル計算 1/2」とそこから参照されている関連記事達は、テンソル計算で出てくるストリング図のテキスト化とテキストによる計算を解説している記事群です。
ストリング図のテンプレート計算
次は、スピヴァック〈David I. Spivak〉のスライド https://math.mit.edu/~dspivak/informatics/talks/WD-IntroductoryTalk.pdf からコピーした絵です。
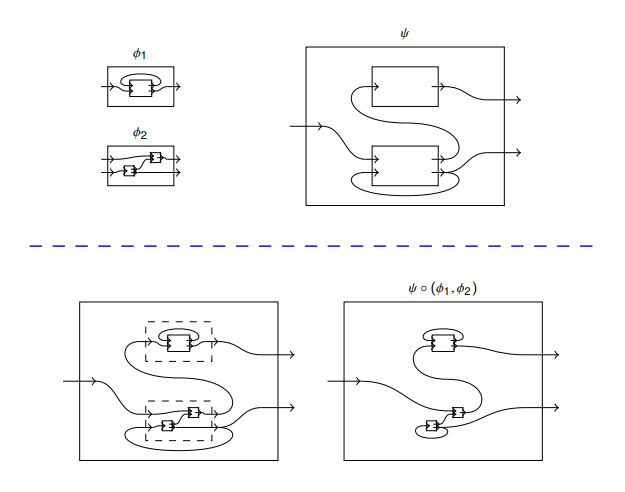
この絵に出てくる内側の箱は穴です。穴があいたキャンバス(外側の四角形はキャンバスの輪郭)にストリング図を描いているわけです。このような絵をスピヴァックはワイヤリング図〈wiring diagram〉と呼んでますが、僕が過去記事でストリング図テンプレート〈string diagram template〉と呼んでいたものと同じです*3。
スピヴァックの絵は、穴が空いたストリング図に対するオペラッド結合〈複圏の結合〉を説明しています。これは要するに、穴に、別な(同じこともある)ストリング図をはめ込むことです。上段はオペラッド結合をする前の状態、下段左はオペラッド結合ではめ込んでいますが、もとの穴が点線で描いてあります。下段右は穴の痕跡を消し去った最終結果です。
このようなはめ込み操作〈オペラッド結合 | 複圏の結合〉の説明は、絵図を使えばさほど難しくはありません。が、テキストだけで記述・説明・計算は出来るでしょうか? もちろん出来るんですが、容易に出来るでしょうか?
スピヴァックの絵の上段右の穴あきストリング図だけを記述するなら、前節の方法が適用できます。今の場合、ワイヤーの型〈ソート | 色〉は全部同じと仮定しているので、ワイヤーを識別する番号または名前を付けていきます。英字小文字の名前〈識別子〉としましょう。それと、穴にも名前が必要なので、こちらは英字大文字で名付けます。例えば次のように。
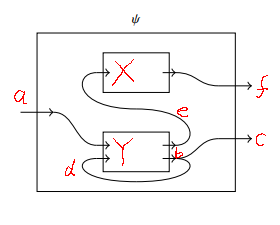
古典テンソル計算と同じ規則で上下添字を使ってテキスト化すると次のようになります。
$`\quad \psi = X_{e}^{f}\, Y_{a\, d}^{e\, b}\, \delta_{b}^{d\, c}`$
$`\delta`$ はクロネッカーのデルタですが、コピーを表すために下付き添字1つ/上付き添字2つです。
繋がり具合が分かりやすいように、古典テンソル計算における「アインシュタインの総和規則」のダミーインデックスである添字は色を変えてみます。
$`\quad \psi = X_{\di{e}}^{f}\, Y_{a\, \di{d}}^{\di{e}\, \di{b}}\, \delta_{\di{b}}^{\di{d}\, c}`$
さて、このようなテキスト表示(別なテキスト表示法でもいいですが)を使って、オペラッド結合の記述や計算もしたいのですが、どうでしょうか? 僕はやる前に気力が萎えています。
クック〈Bob Coecke〉のような先鋭的絵図主義者*4ならば、「そもそもテキスト化なんてやる必要がない!」と言いそうですが、僕の現実的な問題として、次の選択肢からの選択が必要です。
- テキスト化はしないで、毎回(なんらかの方法で)絵を描く。
- テキスト化の規則を確立して、テキストで記述する。
どっちもイヤだ! もっと良い第三の選択肢があるのでしょうか。あって欲しい。