ストリング図と相性が良いテンソル計算 1/2 - 檜山正幸のキマイラ飼育記 (はてなBlog)

ストリング図とテンソル計算については、以下の過去記事で述べました。

ストリング図とテンソル計算：クソバカ丁寧編

上記過去記事では、律儀に愚直にテンソル計算する方法を説明しました。もっと素早く計算する方法があることは記しておきました。

ここまでのプロセスは過剰に丁寧な記述・計算です。うまくサボることにより、もっと素早く記述・計算する方法があります。上下の添字を巧みにあやつる“インデックス・ジャグリング”としての古典テンソル計算は、サボるテクニックを洗練させたものです

“インデックス・ジャグリング”としての古典テンソル計算は成熟した技法ですが、わかりやすくはないし、ストリング図との相性が良くありません。この記事（1/2）と引き続く記事（2/2）では、ストリング図との対応を分かりやすい形にした“インデックス・ジャグリング”を紹介します。「ストリング図とテンソル計算：クソバカ丁寧編」の続きですが、この記事だけでも読めるように一部の内容は繰り返し述べています。

「ストリング図とテンソル計算：クソバカ丁寧編」と本記事／引き続く記事により、ストリング図とテンソル計算は不自由なく扱えるようになることを目指します。$`\newcommand{\Idx}[2]{
{\scriptsize \begin{pmatrix} #1 \\ \downarrow\\ #2\end{pmatrix} } }
\newcommand{\IdxDU}[2]{ % index down-to-up
{\scriptsize \begin{pmatrix} #2 \\ \uparrow\\ #1\end{pmatrix} } }
\newcommand{\conc}{\mathop{\#}}
\newcommand{\bs}[1]{\boldsymbol{#1}}
\require{color}
\newcommand{\di}[1]{\textcolor{orange}{#1} } % dummy index
\newcommand{\dii}[1]{\textcolor{skyblue}{#1} }
\newcommand{\C}{\mathop{;}} % composition
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }%
\newcommand{\For}{\Keyword{For } }%
\newcommand{\Define}{\Keyword{Define } }%
\newcommand{\When}{\Keyword{When } }%
\newcommand{\Then}{\Keyword{Then } }%
%`$

内容：

行列の書き方
テンソルの書き方
テンソル積
結合
例題
古典テンソル計算

関連記事：

行列の書き方

行列は、主に線形写像を表現するために使われ、次のような書き方をします。

$`\quad A = (a_{ji})`$

もとの意味（線形写像）を離れて行列自体を見てみれば、それは実数値関数です。

$`\quad A : I\times J \to {\bf R}`$

関数を表す標準的記法であるラムダ記法で書くなら：

$`\quad A = \lambda\, (i, j)\in I\times J. A(i, j)`$

関数である $`A`$ に引数〈arguments〉$`i, \, j`$ を渡す記法は色々あります。

$`A(i, j)`$
$`A[i, j]`$
$`A_i^j`$
$`A_{ji}`$
$`A(j \mid i)`$

約束さえ決めておけば、どんな書き方をしようとも自由なので、次のような書き方も使っていいとします。書き方は違えど、すべて同じ意味です。

$`A(i \to j)`$
$`A(j \leftarrow i)`$
$`A\Idx{i}{j}`$
$`A\IdxDU{i}{j}`$

ここでは、$`A\Idx{i}{j}`$ を主に使います。この書き方を選ぶのは、上から下に向かって描くストリング図との視覚的類似性からです。

行列を「数を四角形に並べたもの」として考えるときは、$`A\Idx{i}{j}`$ のインデックス $`i`$ が横方向に走るインデックス〈列の番号〉、$`j`$ が縦方向に走るインデックス〈行の番号〉です。今の文脈では「インデックス」と「引数」は同義語です。縦ベクトル $`V`$ 、横ベクトル $`H`$ の成分は次の形に書けます。

$`V\Idx{*}{j}`$
$`H\Idx{i}{*}`$

ここで、アスタリスク $`*`$ は、典型的な単元集合 $`{\bf 1}`$ の唯一の要素を表すリテラル定数です。

$`\quad {\bf 1} = \{*\}`$

なお、$`* = (), {\bf 1} = \{()\}`$ と定義しておくと計算上便利になります。

実数値関数としては $`A:I\times J \to {\bf R}`$ である行列の“行列としてのプロファイル”（行列の圏における域と余域）は、$`I \to J`$ となります。実数値関数としてのプロファイル $`I\times J \to {\bf R} `$ と行列としてのプロファイル $`I \to J`$ は別物です（考えている圏が違うので）。

$`A:I \to J`$ （行列として）
$`V:{\bf 1} \to J`$ （行列として）
$`H:I \to {\bf 1}`$ （行列として）
$`A:I \times J \to {\bf R}`$ （関数として）
$`V:{\bf 1} \times J \to {\bf R}`$ （関数として）
$`H:I \times {\bf 1}\to {\bf R}`$ （関数として）

ラムダ記法とまったく同じ意味で、次のような書き方も使います。

$`
\quad A = \lambda\, (i, j)\in I\times J.\, A\Idx{i}{j} = A\Idx{i}{j}^{i\in I}_{j\in J} = A\Idx{i\in I}{j\in J}\\
\:\\
\quad V = \lambda\, j\in J.\, V\Idx{*}{j} = V\Idx{*}{j}_{j\in J} = V\Idx{*}{j\in J}\\
\:\\
\quad H = \lambda\, i\in I.\, H\Idx{i}{*} = H\Idx{i}{*}^{i\in I}= H\Idx{i\in I}{*}
`$

もっと具体的に、$`A`$ が2列3行の行列なら：

$`
\quad A = \lambda\, (i, j)\in \{1, 2\}\times \{1, 2, 3\}.\, A\Idx{i}{j}
= A\Idx{i}{j}^{i\in \{1, 2\}}_{j\in \{1, 2, 3\}} = A\Idx{i\in \{1, 2\}}{j\in \{1, 2, 3\}}
`$

だいぶ面積を使ってしまいますが、成分を四角形に並べたものとして書き下すと以下のとおり。

$`\quad A =
\begin{bmatrix}
A\Idx{1}{1} & A\Idx{2}{1} \\
A\Idx{1}{2} & A\Idx{2}{2} \\
A\Idx{1}{3} & A\Idx{2}{3}
\end{bmatrix}
`$

$`A\Idx{i}{j}`$ という成分表記は、成分を四角形に並べるより、片方向の完全二部グラフ(下)の有向辺に実数値が乗っているという解釈（メンタルモデル）のほうがシックリくるでしょう。

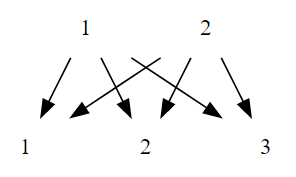
例えば、$`\Idx{2}{1}`$ という有向辺に乗る実数値が $`A\Idx{2}{1}`$ です。有向辺に実数値が乗っているという解釈は、テンソル（次節）でも使い続けられる良いメンタルモデルです。

テンソルの書き方

テンソル〈tensor〉（色々な意味があるが、ここで扱うテンソル）は、行列のインデックス（引数と同じ意味）としてタプルも許したものです。例えば、$`(x, y)\in X\times Y,\, (s, t, u)\in S\times T\times U`$ をインデックスとするテンソル $`B`$ は次の形です。

$`\quad B = B\Idx{(x, y)}{(s, t, u)}^{(x, y)\in X\times Y}_{(s, t, u)\in S\times T\times U}`$

入れ子の括弧がうるさいので、内側の括弧は省略することにして成分を書くと：

$`\quad B\Idx{x, y}{s, t, u}`$

インデックスの集合は必ずしも番号である必要はありません。番号に限定すると、応用上は不便です。例えば、血圧 $`\text{High}, \text{Normal},\text{Low}`$ 、喫煙習慣 $`\text{Smoking}, \text{NoSmoking}`$ の人がとある病気になっているか $`\text{Yes}, \text{No}`$ の統計的データを $`D`$ とすると、次のように書けます。

$`\quad D = D\Idx{b, s}{d}^{b\in \{\text{High}, \text{Normal},\text{Low}\}, s \in \{\text{Smoking}, \text{NoSmoking}\}}_{d\in \{\text{Yes}, \text{No}\} }`$

インデックスであるタプルを一文字で表現するときもあります。例えば、$`\vec{p} = (x, y), \vec{q} = (s, t, u)`$ と置けば：

$`\quad B\Idx{x, y}{s, t, u} = B\Idx{(x, y)}{(s, t, u)} = B\Idx{\vec{p}}{\vec{q}}`$

今はタプルであることを強調して $`\vec{p}, \vec{q}`$ を使いましたが、改めて $`\vec{p}`$ を $`p`$ 、$`\vec{q}`$ を $`q`$ と置けば：

$`\quad B\Idx{x, y}{s, t, u} = B\Idx{p}{q}`$

インデックスの集合も明示すれば：

$`\quad B = B\Idx{p}{q}^{p\in X\times Y}_{q \in S\times T\times U}`$

色々な状況と色々な書き方があることを理解して柔軟に対応してください。

すぐ上に出てきたテンソル $`B`$ の関数としてのプロファイルは

$`\quad B :(X\times Y)\times (S\times T\times U) \to {\bf R}`$

ですが、テンソルとしてのプロファイルは

$`\quad B :(X, Y)\to (S, T, U)`$

と決めます。矢印の前後は“集合のリスト”です。行列のプロファイルの場合も長さ1または長さ0のリストだったと解釈すると辻褄が合います。

$`A:(I) \to (J)`$
$`V:() \to (J)`$
$`H:(I) \to ()`$

プロファイルも上から下に書けば、ストリング図の描画方向と揃います。

$`\quad B :\begin{matrix} (X, Y)\\ \downarrow\\ (S, T, U)\end{matrix}\\
\:\\
\quad A: \begin{matrix}(I) \\ \downarrow\\ (J)\end{matrix}\\
\:\\
\quad V: \begin{matrix}() \\ \downarrow\\ (J)\end{matrix}\\
\:\\
\quad H: \begin{matrix}(I) \\ \downarrow\\ ()\end{matrix}
`$

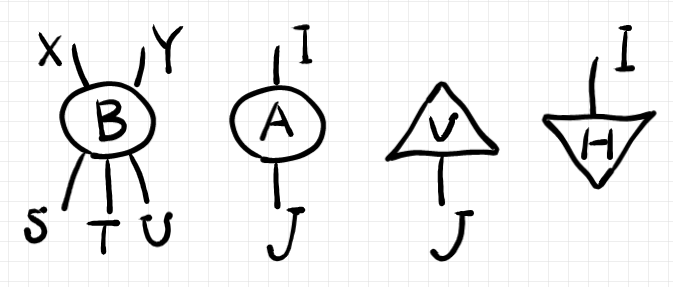
我々は、横に書く（描く）か／縦に書く（描く）かの違い程度でけっこう困惑したり混乱したり、あるいは了解したり納得したりするものです。概念的本質にはまったく影響しない単なる書き方（描き方）の違いに過ぎないのですが*1。

テンソル積

2つのテンソル $`A, B`$ のテンソル積〈tensor product〉は $`A\otimes B`$ と書きます。プロファイルには次の関係があります。

$`\When\\
\quad A: \begin{matrix}\vec{X} \\ \downarrow \\ \vec{Y}\end{matrix}\,,\:
B:\begin{matrix}\vec{S} \\ \downarrow \\ \vec{T}\end{matrix} \\
\Then\\
\quad A\otimes B: \begin{matrix} \vec{X} \conc \vec{S}\\ \downarrow\\ \vec{Y} \conc \vec{T}\end{matrix}
`$

ここで、$`\vec{X}`$ と矢印を付けているのは、集合のリストかも知れないことを強調してです。例えば、$`\vec{X} = (X_1, X_2, \cdots, X_n)`$ 。記号 $`\conc`$ はリストの連接〈concatenation〉を表します。リストの連接もテンソル積の記号で書くなら、次のように統一感があって気持ちいいかも知れません。

$`\quad A\otimes B: \begin{matrix} \vec{X} \otimes \vec{S}\\ \downarrow\\ \vec{Y} \otimes \vec{T}\end{matrix}
`$

集合のリストであってもいつでも矢印を付けるとは限らないので、そこらへんは臨機応変に考えてください。

テンソル積 $`A\otimes B`$ の具体的な（成分による）定義は以下のとおり。

$`\For A = A\Idx{\vec{x}}{\vec{y}}^{\vec{x}\in \prod(\vec{X})}_{\vec{y} \in \prod(\vec{Y})}\\
\:\\
\For B = B\Idx{\vec{s}}{\vec{t}}^{\vec{s}\in \prod(\vec{S})}_{\vec{t} \in \prod(\vec{T}) }\\
\:\\
\Define (A\otimes B)\Idx{\vec{x}\conc\vec{s}}{\vec{y}\conc\vec{t}} :=
A\Idx{\vec{x}}{\vec{y}} B\Idx{\vec{s}}{\vec{t}}
`$

ここで、$`\prod(\vec{X})`$ は、集合のリストである $`\vec{X}`$ の総直積を表し、$`\vec{x}`$ はその要素であるタプルです。例えば：

$`\When\\
\quad \vec{X} = (X_1, X_2, \cdots, X_n)\\
\quad \prod(\vec{X}) = \prod( (X_1, X_2, \cdots, X_n)) = X_1\times X_2 \times \cdots \times X_n\\
\quad \vec{x} = (x_1, x_2, \cdots, x_n)\\
\Then\\
\quad \vec{x} \in \prod(\vec{X})\\
\iff (x_1, x_2, \cdots, x_n) \in X_1 \times X_2 \times \cdots X_n`$

$`\vec{x}\conc\vec{s}`$ はタプルの連接です。例えば：

$`\When\\
\quad \vec{x} = (x_1, x_2, \cdots, x_n)\\
\quad \vec{s} = (s_1, s_2, \cdots, x_l)\\
\Then\\
\quad \vec{x}\conc\vec{s} = (x_1, x_2, \cdots, x_n)\conc(s_1, s_2, \cdots, x_l)\\
\qquad = (x_1, x_2, \cdots, x_n, s_1, s_2, \cdots, x_l)
`$

タプルの連接は次のどれで書いてもいいとします。

$`\vec{x}\conc \vec{y}`$
$`\vec{x}\, \vec{y}`$
$`\vec{x},\vec{y}`$

丁寧に書くと記号が煩雑になるので、単純なケースを簡潔に書けば次のようです。

$`\Define (A\otimes B)\Idx{x\, s}{y\,t} :=
A\Idx{x}{y} B\Idx{s}{t}
`$

これは次のストリング図に対応します。

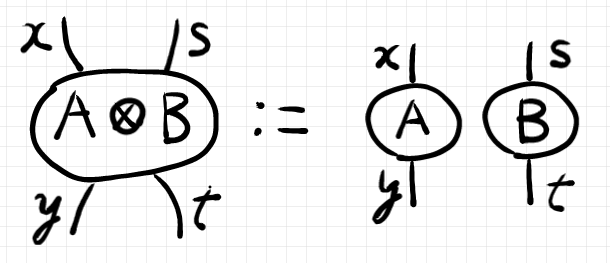
結合

2つのテンソル $`A, B`$ の結合〈composition | 合成〉は $`A\C B`$ と書きます。プロファイルには次の関係があります。以下、前節の最後の定義と同様に簡潔な記法で書きます。

$`\When\\
\quad A: \begin{matrix}X \\ \downarrow \\ Y\end{matrix}\,,\:
B:\begin{matrix}Y \\ \downarrow \\ Z\end{matrix} \\
\Then\\
\quad A\C B: \begin{matrix} X \\ \downarrow\\ Z \end{matrix}
`$

結合 $`A\C B`$ の具体的な（成分による）定義は次のようです。

$`\For A = A\Idx{x}{y}^{x\in X}_{y \in Y}\\
\:\\
\For B = B\Idx{y}{z}^{y\in Y}_{z \in Z }\\
\:\\
\Define (A\C B)\Idx{x}{z} :=
{\displaystyle \sum_{y\in Y}} A\Idx{x}{y}B\Idx{y}{z}
`$

さてここで、古典テンソル計算で「最も重要なテクニック〈トリック〉」とも言える、総和記号の省略規則〈アインシュタインの総和規約 | Einstein summation convention〉を導入します。

同じインデックスが上下に出現しているときは、そのインデックスに渡って和を取るものとして、総和記号は省略する。

総和記号は省略しますが、和を取るためのダミー・インデックスは色を変えて分かりやすくすることにします。総和記号を省略すると：

$`\Define (A\C B)\Idx{x}{z} :=
A\Idx{x}{\di{y}}B\Idx{\di{y}}{z}
`$

$`\di{y}`$ が和を取るためのダミー・インデックスで、総和記号は省略されています。これは次のストリング図に対応します。

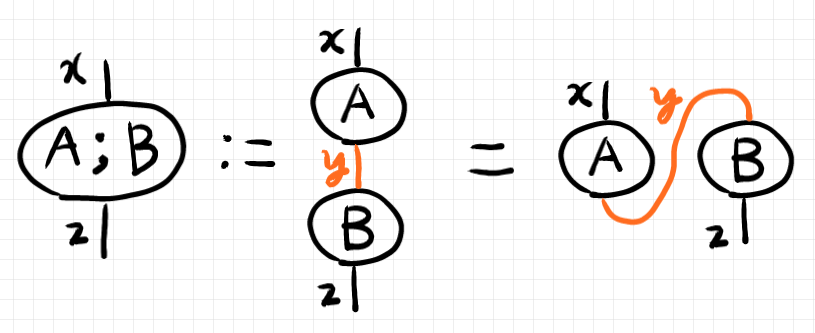
例題

次のような3つのテンソルを考えます。

$`
\quad P = P\Idx{*}{x}_{x\in X}\\
\:\\
\quad F = F\Idx{x}{y}^{x\in X}_{y\in Y}\\
\:\\
\quad G = G\Idx{x, y}{z}^{x\in X, y\in Y}_{z\in Z}
`$

$`(P \otimes F)\C G`$ の成分表示を求めます。$`(P \otimes F)\C G`$ をストリング図で描けば次のようです。

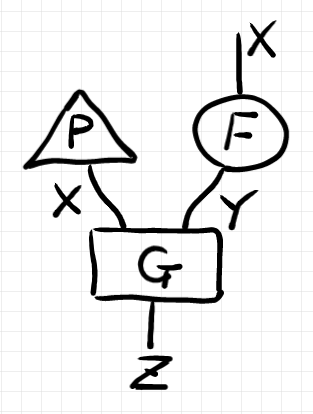
まず、$`P \otimes F`$ の成分は次のように書けます。

$`\quad (P \otimes F)\Idx{x}{x', y} = P\Idx{*}{x'} F\Idx{x}{y}`$

ここで、$`x`$ とは別な文字 $`x'`$ を導入しているのは、$`P\Idx{*}{x} F\Idx{x}{y}`$ と書くと $`x`$ に関して総和を取ることになってしまうからです(すぐ下参照)。

$`\quad P\Idx{*}{x} F\Idx{x}{y}\\
\:\\
= P\Idx{*}{\di{x}} F\Idx{\di{x}}{y}\\
\:\\
= {\displaystyle \sum_{x\in X}}P\Idx{*}{x} F\Idx{x}{y}`$

次に、$`(P \otimes F)\C G`$ の成分を書き下します。今度は、インデックスを同じ文字にすることによって総和を取ります。

$`\quad ( (P \otimes F)\C G)\Idx{x}{z} = \left(P\Idx{*}{\di{x'}} F\Idx{x}{\di{y}} \right) G\Idx{\di{x'}, \di{y}}{z}`$

括弧は省略して単に

$`\quad P\Idx{*}{\di{x'}} F\Idx{x}{\di{y}} G\Idx{\di{x'}, \di{y}}{z}`$

でもかまいません。このテキスト記法のレイアウトに似せて描いたストリング図は次のようです。

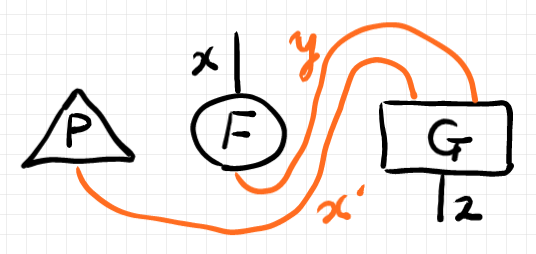
総和記号を明示的に書くなら：

$`\quad {\displaystyle \sum_{x'\in X, y\in Y}} P\Idx{*}{x'} F\Idx{x}{y} G\Idx{x', y}{z}`$

古典テンソル計算

この記事で導入した記法と、標準的な古典テンソル計算の記法の違いを説明しておきます。

古典テンソル計算でも上下のインデックスを使いますが、この記事とは上下が逆です。インデックスの書き方はシンプルで、テンソルとテンソルの成分を区別しません。インデックスの集合は暗黙化され明示されません。前節の例の3つのテンソルは、古典テンソル計算では次のように書きます。

$`
\quad P = P^x\\
\quad F = F_x^y\\
\quad G = G_{x y}^{z}
`$

結合は反図式順なので、次のようになります。

$`\quad ( G \circ (P \otimes F))_x^z = G_{x' y}^z P^{x'} F_x^y`$

総和記号を明示的に書くなら：

$`\quad {\displaystyle \sum_{x'\in X, y\in Y}} G_{x' y}^z P^{x'} F_x^y`$

非常にコンパクトに書けるので素早く筆記できるメリットがあります。が、いきなりこの記法を出されると解釈に苦しむのではないでしょうか。ストリング図との対応に慣れた後なら、速記法としての古典テンソル計算記法は便利だと思います。

幾つもの書き方で計算してみると、最終的には「書き方なんてどうでもいい」という“悟り”が得られるでしょう。

続き：ストリング図と相性が良いテンソル計算 2/2

*1:認知的な観点から言えば、“単なる書き方（描き方）の違い”は重要で、それにより了解・納得の難易度が大きな影響を受けることになります。