ここで言うテンソルは、圏論的に言えば、モノイド圏やトレース付きモノイド圏の射のことです。幾つかのインデックス〈添字〉が付いた配列みたいなモノと思ってもいいです。絵に描くと、脚〈legs〉が出た“テンソルボックス”達をワイヤーで繋いだ図形になります。脚がたくさんあったり、複雑なワイヤリングをすることもあります。
テンソルの計算法則の絵をまとめたものがないかと探したら、意外に見つからない。なので、手描きで描いてみました。トレース(ワイヤーをループ状にする操作)は含まれていませんが、他の演算と法則は絵にしています。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\hyp}{\text{-} }
\newcommand{\id}{\mathrm{id} }
\newcommand{\DA}{ \!\downarrow }
\newcommand{\UA}{ \!\uparrow }
`$
内容:
関連する過去記事:
テンソルの結合〈合成〉
テンソル(射や複射や多射)の結合〈合成 | composition〉は縦方向、上から下に描きます。結合法則〈associative law〉、左単位法則〈left unit law〉、右単位法則〈right unit law〉は以下のとおり。黒丸〈ドット〉は恒等〈identity〉です。
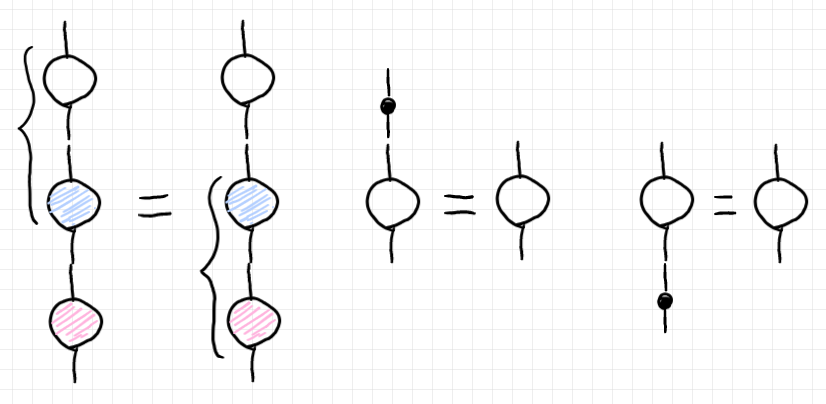
テンソル〈射/複射/多射〉のプロファイルを以下のように設定します。
$`\quad f: A \to B\\
\quad g: B \to C\\
\quad h: C \to D
`$
この設定で、計算法則をテキストで書き下すと:
$`\quad (f;g); h = f;(g;h)\\
\quad \id_A; f = f\\
\quad f; \id_B = f`$
反図式順結合記号〈anti-diagrammatic order composition symbol〉'$`\circ`$' を使うと:
$`\quad h\circ (g \circ f) = (h\circ g) \circ f\\
\quad f \circ \id_A = f\\
\quad \id_B\circ f = f`$
図式順か反図式順かで、「左単位法則」「右単位法則」が何を指すかが変わってしまうことに注意してください(ショーモナイ話だけど)。
変数〈インデックス | 添字〉を次のように導入します。束縛変数も列挙します。
$`\quad a, a' : A\\
\quad b,b' : B\\
\quad c : C\\
\quad d : D
`$
たくさんの変数を使うときにカンマだけでは記述不可能になるので、区切り記号をカンマではなくて矢印を使うことにして、変数と総和記号を使って計算法則を記述すると:
$`\quad \sum_{c\in C}(\sum_{b\in B}f(a \to b)\, g(b \to c))\, h(c\to d)\\
\quad = \sum_{b\in B} f(a \to b)\, (\sum_{c\in C} g(b \to c)\, h(c\to d) )\\
\quad \sum_{a' \in A}\delta(a \to a')\, f(a' \to b) = f(a\to b)\\
\quad \sum_{b' \in B}f(a \to b)\, \delta(b' \to b) = f(a\to b)
`$
$`\delta(\hyp \to \hyp)`$ は恒等に対応するデルタテンソルです。
たくさんの変数を使う例を挙げておきます。記法を揃えるために、対象(集合と思ってよい)のテンソル積にも(実際は '$`\times`$' であったとしても) '$`\otimes`$' を使います。
$`\quad (a_1, a_2, a_3), ({a'}_1, {a'}_2, {a'}_3) : A_1\otimes A_2 \otimes A_3 \:(A = A_1\otimes A_2 \otimes A_3)\\
\quad b, b' : B\\
\quad (c_1, c_2) : C_1 \otimes C_2 \:(C = C_1 \otimes C_2)\\
\quad d : D\\
\:\\
\quad \sum_{(c_1, c_2) \in C}(\sum_{b\in B}f(a_1, a_2, a_3 \to b)\, g(b \to c_1, c_2))\, h(c_1, c_2 \to d)\\
\quad = \sum_{b\in B} f(a_1, a_2, a_3 \to b)\, (\sum_{(c_1, c_2)\in C} g(b \to c_1, c_2)\, h(c_1, c_2\to d) )\\
\quad \sum_{({a'}_1, {a'}_2, {a'}_3 )\in A}\delta(a_1, a_2, a_3 \to {a'}_1, {a'}_2, {a'}_3)\, f({a'}_1, {a'}_2, {a'}_3 \to b)\\
\quad = f(a_1, a_2, a_3 \to b)\\
\quad \sum_{b' \in B}f(a_1, a_2, a_3 \to b')\, \delta(b' \to b) = f(a_1, a_2, a_3 \to b)
`$
ここで、書き方を次のように変えます。
$`\quad f\UA_a^b = f(a \to b)`$
そして、反図式順の方向(右から左)に合わせると、計算法則は次のようになります。
$`\quad \sum_{c\in C} h\UA_c^d\, (\sum_{b\in B} g\UA_b^c \, f\UA_a^b )\\
\quad = \sum_{b\in B} (\sum_{c\in C} h\UA_c^d\, g\UA_b^c )\, f\UA_a^b\\
\quad \sum_{a' \in A} f\UA_{a'}^b \, \delta\UA_a^{a'} = f\UA_a^b\\
\quad \sum_{b' \in B} \delta\UA_{b'}^b\, f\UA_a^{b'} = f\UA_a^b`$
伝統的テンソル計算の書き方は、'$`\uparrow`$' は付かず、総和記号を省略します。
$`\quad h_c^d\, ( g_b^c \, f_a^b ) = ( h_c^d\, g_b^c )\, f_a^b\\
\quad f_{a'}^b \, \delta_a^{a'} = f_a^b\\
\quad \delta_{b'}^b\, f_a^{b'} = f_a^b`$
たくさんの変数を使う場合なら次のようです。
$`\quad h_{c_1\, c_2}^d\, ( g_b^{c_1\, c_2} \, f_{a_1\, a_2\, a_3}^b ) = ( h_{c_1\, c_2}^d\, g_b^{c_1\, c_2} )\, f_{a_1\, a_2\, a_3}^b\\
\quad f_{ {a'}_1\, {a'}_2\, {a'}_3}^b \, \delta_{a_1\, a_2\, a_3}^{{a'}_1\, {a'}_2\, {a'}_3} = f_{a_1\, a_2\, a_3}^b\\
\quad \delta_{b'}^b\, f_{a_1\, a_2\, a_3}^{b'} = f_{a_1\, a_2\, a_3}^b`$
テンソルのテンソル積
テンソルのテンソル積は横方向、左から右に描きます。テンソル積に関する結合法則、左単位法則、右単位法則は以下のとおり。“点線に黒丸”は単位対象〈unit object〉の恒等*1で、$`\id_I`$ と書きます。その実体はスカラーのイチです*2。
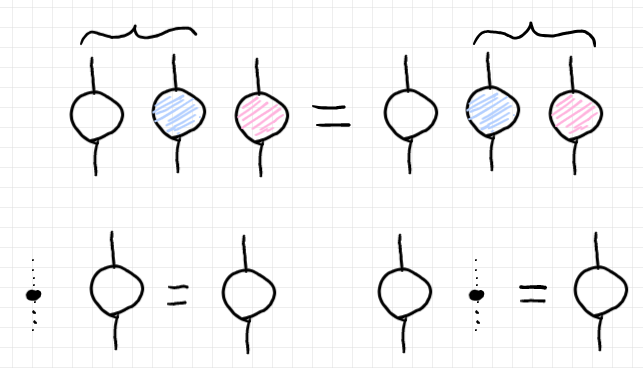
テンソルのプロファイルは以下のように設定します。
$`\quad f: A \to B\\
\quad g: C \to D\\
\quad h: X \to Y
`$
計算法則*3をテキストで書き下すと:
$`\quad (f\otimes g)\otimes h = f\otimes (g\otimes h)\\
\quad \id_I \otimes f = f\\
\quad f\otimes \id_I = f`$
変数を次のように導入します。
$`\quad a : A\\
\quad b : B\\
\quad c : C\\
\quad d : D\\
\quad x : X\\
\quad y : Y
`$
変数を使って計算法則を記述すると:
$`\quad (f(a \to b)\, g(c \to d))\, h(x \to y) =
f(a \to b)\, (g(c \to d)\, h(x \to y) )\\
\quad 1\, f(a\to b) = f(a \to b)\\
\quad f(a\to b)\, 1 = f(a \to b)
`$
書き方を次のように変えます。
$`\quad f\UA_a^b = f(a \to b)`$
計算法則は次のようになります。
$`\quad (f\UA_a^b\, g\UA_c^d)\, h\UA_x^y = f\UA_a^b\, (g\UA_c^d\, h\UA_x^y )\\
\quad 1\, f\UA_a^b = f\UA_a^b\\
\quad f\UA_a^b\,1 = f\UA_a^b
`$
伝統的テンソル計算の書き方なら:
$`\quad (f_a^b\, g_c^d)\, h_x^y = f_a^b\, (g_c^d\, h_x^y )\\
\quad 1\, f_a^b = f_a^b\\
\quad f_a^b\,1 = f_a^b\
`$
法則を変数を使って成分ごとに記述すると、テンソル積の法則はスカラーに関する法則に帰着します。
交替法則
テンソルの結合とテンソル積に関する交替法則〈interchange law〉は以下のとおり。横割り計算と縦割り計算の結果が等しいことを主張します。右側の法則は交替法則と関係無いように見えますが、圏論的には仲間(双関手性)の法則です。
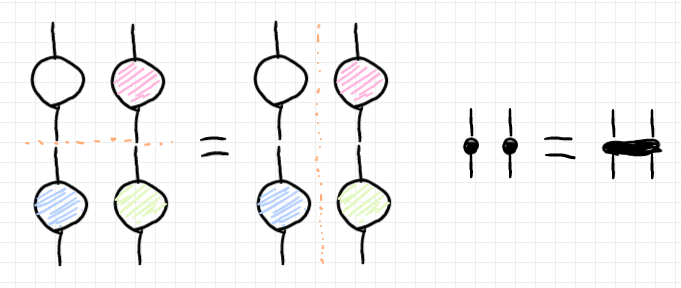
テンソルのプロファイルは以下のように設定します。
$`\quad f: A \to B\\
\quad g: B \to C\\
\quad h: X \to Y \\
\quad k: Y \to Z
`$
計算法則をテキストで書き下すと:
$`\quad (f \otimes h);(g \otimes k ) = (f ; g) \otimes (h ; k)\\
\quad \id_A \otimes \id_B = \id_{A\otimes B}
`$
変数を次のように導入します。
$`\quad a, a' : A\\
\quad b, b' : B\\
\quad c : C\\
\quad x : X\\
\quad y : Y\\
\quad z : Z
`$
変数を使って計算法則を記述すると:
$`\quad \sum_{(b, y) \in B\otimes Y} ( f(a \to b)\, h(x\to y)) (g(b\to c) \, k(y\to z) ) \\
\quad = (\sum_{b\in B} f(a \to b) \, g(b \to c) ) (\sum_{y\in Y} h(x \to y) \, k(y \to z))\\
\quad \delta(a \to a')\, \delta(b \to b') = \delta( a, b \to a', b' )
`$
書き方を次のように変えます。
$`\quad f\UA_a^b = f(a \to b)`$
計算法則は次のようになります。
$`\quad \sum_{(b, y) \in B\otimes Y} (g\UA_b^c \, k\UA_y^z ) ( f\UA_a^b \, h\UA_x^y ) \\
\quad = (\sum_{b\in B} g\UA_b^c \, f\UA_a^b ) (\sum_{y\in Y} k\UA_y^z \, h\UA_x^y)\\
\quad \delta\UA_a^{a'} \delta\UA_b^{b'} = \delta\UA_{a,b}^{a', b'}
`$
伝統的テンソル計算の書き方なら:
$`\quad (g_b^c \, k_y^z ) ( f_a^b \, h_x^y ) = ( g_b^c \, f_a^b ) ( k_y^z \, h_x^y)\\
\quad \delta_a^{a'} \delta_b^{b'} = \delta_{a\,b}^{a'\, b'}
`$
エレベーター法則
交替法則から出る定理なのですが、次の法則(エレベーター法則)は便利に使えます。
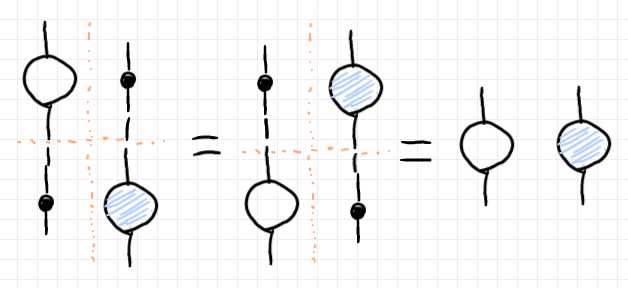
テンソルのプロファイルは以下のように設定します。
$`\quad f: A \to B\\
\quad g: C \to D
`$
計算法則をテキストで書き下すと:
$`\quad (f \otimes \id_C);(\id_B \otimes g ) = (\id_A \otimes g) ; (f \otimes \id_D) = f\otimes g
`$
縦割り計算の形で書くと自明な等式になります。
$`\quad (f ; \id_B)\otimes (\id_C ; g) = (\id_A ; f)\otimes (g ; \id_D) = f\otimes g
`$
変数を次のように導入します。
$`\quad a, a' : A\\
\quad b, b' : B\\
\quad c, c' : C\\
\quad d, d' : D
`$
変数を使って計算法則を記述すると:
$`\quad \sum_{(b', c')\in B\otimes C} (f(a \to b') \, \delta(c \to c') ) (\delta(b' \to b) \, g(c'\to d) ) \\
\quad = \sum_{(a', d')\in A\otimes D}(\delta(a \to a') \, g(c \to d')) (f(a' \to b) \, \delta(d' \to d))\\
\quad = f(a \to b)\, g(c\to d)
`$
書き方を次のように変えます。
$`\quad f\UA_a^b = f(a \to b)`$
計算法則は次のようになります。
$`\quad \sum_{(b', c')\in B\otimes C} (\delta\UA_{b'}^b \, g\UA_{c'}^d )( f\UA_a^{b'} \, \delta\UA_c^{c'} ) \\
\quad = \sum_{(a', d')\in A\otimes D} (f\UA_{a'}^b \, \delta\UA_{d'}^d) (\delta\UA_a^{a'} \, g\UA_c^{d'})\\
\quad = f\UA_a^b\, g\UA_c^d
`$
伝統的テンソル計算の書き方なら:
$`\quad (\delta_{b'}^b \, g_{c'}^d )( f_a^{b'} \, \delta_c^{c'} )
= (f_{a'}^b \, \delta_{d'}^d) (\delta_a^{a'} \, g_c^{d'}) = f_a^b\, g_c^d
`$
入れ子の図とワイヤーのバンチ・分離
ストリング図のなかのひとつのテンソルボックスが、内部にまたストリング図を持っていることがあります。これはまた、ストリング図の一部分を境界線で囲って、ひとつのボックスのように取り扱っているとも言えます。そのようなとき、ストリング図は入れ子の図になっています。
ストリング図のなかの一本のワイヤーが、実は複数のワイヤーの束〈たば〉であることがあります。複数のワイヤーを明示的にバンチして〈一括して〉束ねる状況を描けば以下のようです。
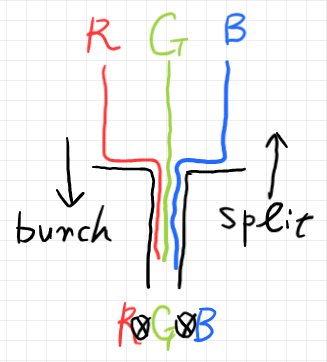
上から下だとバンチ〈一括〉で、下から上に見れば一本のワイヤーを複数のワイヤーに分解・分離しています。
毎度毎度色を付けたりリアルなケーブル(ワイヤーの束)を描くのは面倒なので、次のように描いてもいいとします。
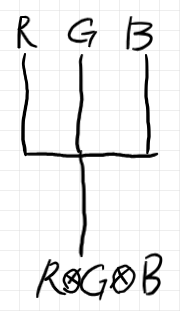
バンチ〈一括〉と分離のプロファイルは次のようです。
$`\quad (R, G, B) \to (R\otimes G\otimes B)\\
\quad (R\otimes G\otimes B) \to (R, B, B)
`$
変数のバンチは、複数の変数達を単一の変数に置き換えることです。バンチされた変数の成分を取り出せば、もとの個別変数が再現します。
$`\quad r: R,\; g:G,\; b:B\\
\quad (r, g, b) \in R\otimes G\otimes B\\
\quad x \in X \: (X := R\otimes G\otimes B)\\
\quad x_1: R,\; x_2:G,\; x_3:B
`$
恒等を取り除く
恒等(絵では黒いドット)は取り除いてかまいません。
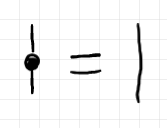
例えば、次のような等式が成立します。

テンソルのプロファイルと変数の名前を決めて、等式をテキストに書き下すと次のようになります。
$`\quad f : (A, B, C) \to (D, E)\\
\quad a: A\\
\quad b, b': B\\
\quad c: C\\
\quad d: D\\
\quad e: E\\
\:\\
\quad \delta(b \to b')\, f(a, b', c \to d, e) = f(a, b, c \to d, e)\\
\text{or}\\
\quad \delta_b^{b'}\, f_{a\, b'\, c}^{d\, e} = f_{a\, b\, c }^{d\, e}\\
`$
$`\delta`$ を消していますが、そのとき変数名の書き換え〈リネーム | リラベル〉が生じます。
次の絵も、同様に恒等のドットを取り除いています。
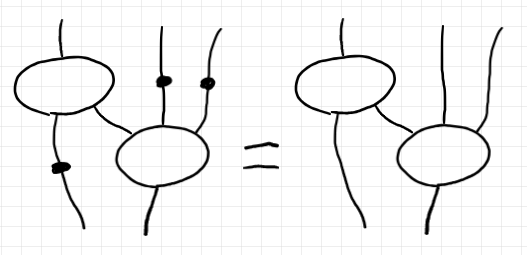
これもテキストに書き下してみます。
$`\quad f : (A) \to (B, C)\\
\quad g : (C, X, Y) \to Z\\
\quad a:A\\
\quad b, b':B\\
\quad c:C \\
\quad x, x':X\\
\quad y, y':Y\\
\quad z:Z\\
\:\\
\quad \sum_{(b', c, x', y')\in B\otimes C\otimes X\otimes Y}
(f(a \to b', c)\, \delta(x \to x')\, \delta(y \to y') )
(\delta(b'\to b)\, g(c, x', y' \to z))\\
\quad = \sum_{c \in C}f(a, b\to c )\, g(c, x, y \to z)\\
\text{or}\\
\quad (f_a^{b'\, c}\, \delta_x^{x'}\, \delta_y^{y'} )
(\delta_{b'}^b\, g_{c\, x'\, y'}^z)\\
\quad = f_{a\, b}^c\, g_{c\, x\, y}^z
`$
慣れれば、ストリング図を見てチャッチャと簡略なテキストに書き下せます。素早い書き取りよりは、計算プロセスをクソバカ丁寧に追いかけたい人は次の記事を参照してください(過去記事ではワイヤーベンディングも扱っています)。
まとめ(絵の寄せ集め)
テンソルの結合〈composition〉の法則達

テンソルのテンソル積〈tensor product〉法則達
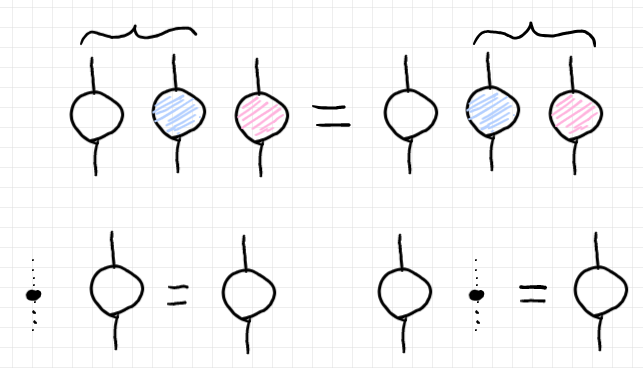
テンソルの結合とテンソル積の両方に関わる法則達


*1:点線は描かなくてもかまいません。むしろ、単位対象は描かないほうが整合的でスッキリします。
*2:圏論的なスカラーとは、単位対象の自己射のことです。
*3:テンソル積〈モノイド積〉の associator, unitor は省略します。厳密モノイド圏で考えていると思ってください。
*4:記事: http://www.aim-ele.co.jp/tech/metal-tech15/ 画像: http://www.aim-ele.co.jp/tech/metal-tech15/images/hifuku.jpg
