状態遷移系やオートマトンをレンズで記述しようとすると、どうも“痒い”ところがあります。テレオロジー圏に、双対的な同語反復射を追加した圏を構成すると、状態遷移系/オートマトンの記述には都合が良さそうです。
思い付いただけで、あまり確認・吟味はしてませんが、とりあえず備忘のためにメモ書きを残しておきます。$`\newcommand{\cat}[1]{\mathcal{#1} }
\newcommand{\op}{\mathrm{op}}
\newcommand{\id}{\mathrm{id}}
\newcommand{\In}{\text{ in }}
\newcommand{\lact}{\mathop{\bullet} }
\newcommand{\J}{\mathrm{J} }
\newcommand{\Iff}{\Leftrightarrow }
\require{color}
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }%
\newcommand{\For}{\Keyword{For } }%
\newcommand{\Where}{\Keyword{Where } }%
%`$
内容:
テレオロジー圏
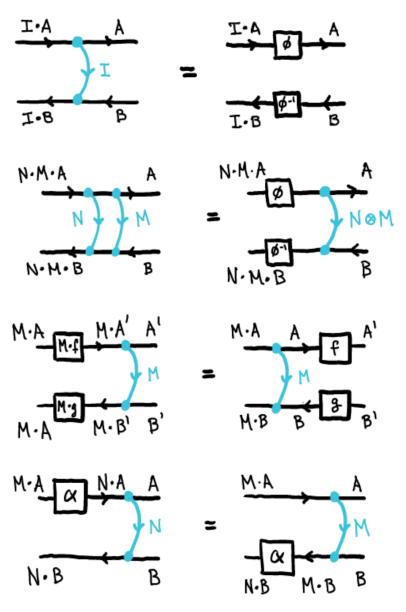
テレオロジー圏〈teleological category〉については、次の過去記事で述べています。
テレオロジー圏はヘッジーズ〈Jules Hedges〉*1によって導入されましたが、ここではロマン〈Mario Roman〉の定義を採用します。レンズやオプティックについて、ある程度の知識は仮定します -- これについては、次の記事からはじまるシリーズで解説しています。
以下の記号は「圏論的レンズ 4: テレオロジー圏」と同じ意味で使います。
- 対称モノイド圏 $`\cat{M}=(\cat{M},\otimes,I,\alpha,\lambda,\rho, \sigma)`$ (記号の乱用)
- 圏 $`\cat{C}`$
- 左モノイド作用 $`(\lact) : \cat{M}\times \cat{C} \to \cat{C}`$
- 圏 $`\cat{T}`$
埋め込み関手 $`\iota`$ は考えずに、$`\cat{C}\times \cat{C}^\op`$ は 圏 $`\cat{T}`$ の広い部分圏〈wide subcategory〉だと仮定します。
$`\quad \cat{C}\times \cat{C}^\op \subseteq \cat{T}\\
\quad |\cat{C}\times \cat{C}^\op| = | \cat{T} |
%`$
部分圏の包含関手を $`\J`$ とします($`\iota`$ と $`\J`$ は事実上同じと思ってかまいません)。
$`\quad \J : \cat{C}\times \cat{C}^\op \to \cat{T} \In {\bf CAT}`$
$`\cat{C}\times \cat{C}^\op`$ の対象や射を表すために、ブラケットで囲んだペアを使うことにします。
$`\quad [f_1, f_2] : [A_1, A_2] \to [B_1, B_2] \In \cat{C}\times \cat{C}^\op\\
\Iff\\
\quad f_1 : A_1 \to B_1 \In \cat{C}\\
\quad f_2 : B_2 \to A_2 \In \cat{C}
%`$
第一成分と第二成分の向きが逆であることに注意してください。このことを強調して、$`\cat{C}\times \cat{C}^\op`$ の対象や射を順逆ペア〈forward-backward pair〉と呼びましょう。ブラケットが順逆ペアの目印です。
さらに、記号の乱用で $`A = [A, A'], f = [f, f']`$ のように書きます。順逆ペアとその第一成分(順方向)に同じ記号を使い、第二成分(逆方向)はダッシュ〈プライム〉を付ける約束です。
$`\quad f : A \to B \In \cat{C}\times \cat{C}^\op\\
\Iff\\
\quad f : A \to B \In \cat{C} \:\:(f,A,B \text{ はオーバーロード})\\
\quad f' : B' \to A' \In \cat{C}
%`$
記号の乱用がたいていそうであるように、この記法は便利ですが、誤認や混乱のリスクはあります。注意してください。
同語反復射の族は次の形に書きます。
$`\For M \in |\cat{M}|\\
\For A = [A, A']\in |\cat{C}\times \cat{C}^\op|\\
\quad \varepsilon^M_A = \varepsilon^M_{[A, A']} : [M\lact A, M\lact A']\to [A, A'] \In \cat{T}
%`$
$`\varepsilon`$ を使ったのは、同語反復射がコンパクト閉圏の余単位に少し似ているからです。添字を上下に分けたのは、そのほうが法則の記述がスッキリするからです。
以上でテレオロジー圏を構成する素材はすべて揃いました。法則〈等式的公理〉は絵〈ストリング図〉で示すのが分かりやすいでしょう。
同語反復射は次のように描きます。
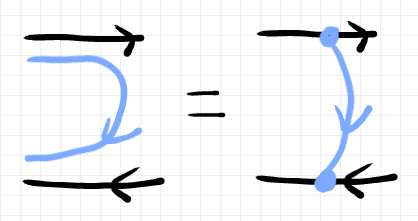
ストリング図上段の右向きワイヤーは $`\cat{C}`$ の射、下段の左向きワイヤーは $`\cat{C}^\op`$ の射、水色のワイヤーは $`\cat{M}`$ の射で曲がっています。上記イコールの右辺はロマンの描画法です。
上段の $`M\lact A`$ に関しては、図の「下から上」の方向がテキストの「左から右」です。下段の $`M\lact A'`$ に関しては、図の「上から下」の方向がテキストの「左から右」です。$`\cat{C}`$ の射の進行方向に向かって右手側がテキストの「左」です(苦笑)。このテの約束ごとの不整合は避けようがない(必ず生じる)ので、各自でアドホックに調整して納得してください。
さて、テレオロジー圏の法則ですが、「圏論的レンズ 4: テレオロジー圏 // テレオロジー圏の定義」の該当箇所を下に引用します。より詳しい説明は元の過去記事を読んでください。
ロマンは、ヘッジズのオリジナルとはだいぶ違った形の定義を提案しています。
- Title: Composing optics
- Author: Mario Roman
- Date: February 6, 2020
- Pages: 21p
- URL: https://www.ioc.ee/~mroman/data/notes/composingoptics.pdf
同語反復射には次の4つの公理〈法則〉を要求します(ロマン論文 p.15 からコピー)。
図のなかのラベルがオーバーロードされて(同じ文字が違う意味で使われて)いてわかりにくいですね。3番目の等式の左辺下側のラベル $`M\lact A`$ は $`M\lact B`$ の間違いです。
トレース付きモノイド圏の法則
以下は、長谷川真人さんの "Recursion from Cyclic Sharing: Traced Monoidal Categories and Models of Cyclic Lambda Calculi (1997)" からコピーした絵です。長谷川さんの描画方向は、射の向きが左から右、モノイド積の方向は下から上です。2010年の記事「トレース付き対称モノイド圏とはこんなモノ」、「トレース付きモノイド圏の新しい定義」において引用しました。
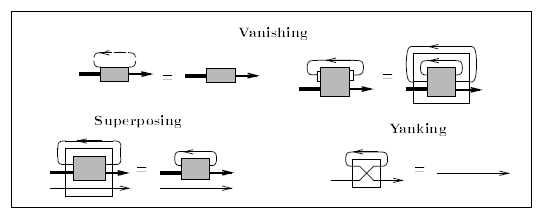
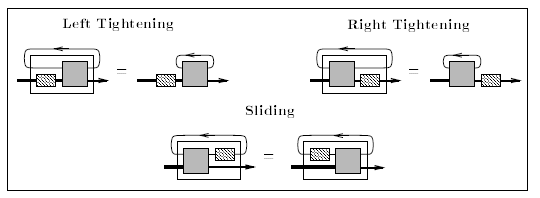
トレース付きモノイド圏の法則(公理)は、バニシング、スーパーポージング、ヤンキング、左右のタイトニング、スライディングです。2つの法則を、どちらもバニシングと呼んでいるので、片方(右側のほう)をバンドリング〈bundling〉としましょう。
これらの法則を列挙すると:
- バニシング〈Vanishing〉
- バンドリング〈Bundling〉
- スーパーポージング〈Superposing〉
- ヤンキング〈Yanking〉
- 左タイトニング〈Left Tightening〉
- 右タイトニング〈Right Tightening〉
- スライディング〈Sliding〉
トレース付きモノイド圏の法則をここに引き合いに出したのは、テレオロジー圏の法則に名前を付けたいからです。
前節のテレオロジー圏の法則を上から順に次の名前で呼びます。
- 右バニシング
- 右バンドリング
- 右タイトニング
- 右スライディング
「右」は、ロマン達が使っている描画の約束における「右」であり、必然的な意味はありません! 右しかないなら「右」と付ける必要はないのですが、次節で「左」法則を導入します。
両側テレオロジー圏
通常のテレオロジー圏(ヘッジーズ/ロマンの意味のテレオロジー圏)に、双対的な同語反復射を追加した圏として両側テレオロジー圏〈two-sided teleological category〉を定義しましょう。
追加する素材は余同語反復射〈cotautological morphism〉の族です。次の形で書きます。
$`\For X \in |\cat{M}|\\
\For A = [A, A'] \in |\cat{C}\times \cat{C}^\op|\\
\quad \eta^X_A = \eta^X_{[A, A']} : [A, A'] \to [X\lact A, X\lact A'] \In \cat{T}
%`$
$`\eta`$ を使ったのは、コンパクト閉圏の単位に似ているからです。
余同語反復射に関して、テレオロジー圏の法則の“左バージョン”を要求します。
- 左バニシング
- 左バンドリング
- 左タイトニング
- 左スライディング
さらに、同語反復射(右で曲がる)と余同語反復射(左で曲がる)の関係として、次の法則も要求します。
- 上ヤンキング〈Upside Yanking〉
- 下ヤンキング〈Downside Yanking〉
- オーバーラッピング〈Overlapping〉
- ループムービング〈Loop Moving〉
追加の法則を絵で描くと次のようです。
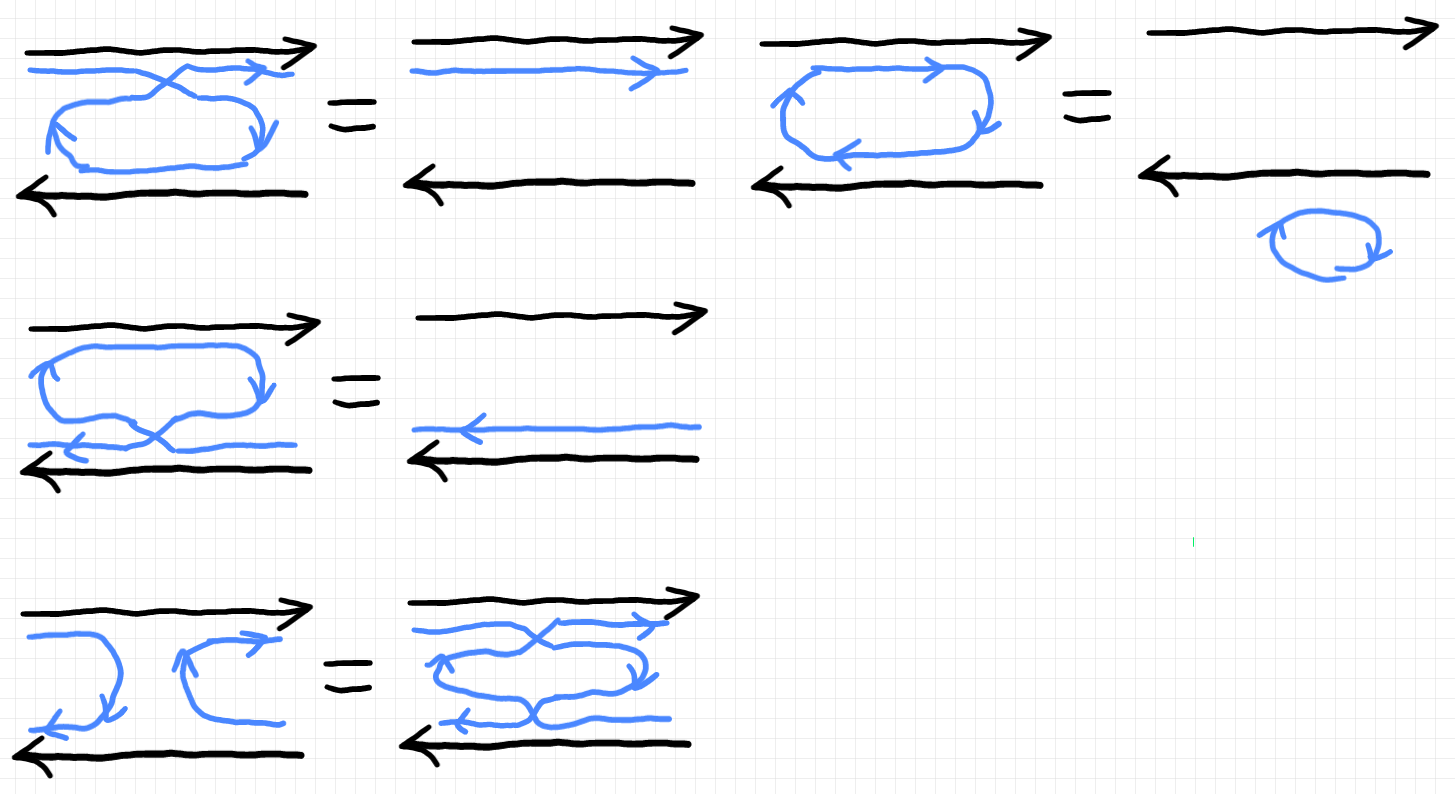
これらの法則は現時点では作業仮説で、「だいたい、こんなもんだろ」で設定しています。
- 上下のヤンキングは、トレース付きモノイド圏のヤンキングと同じです。
- オーバーラッピングは、同語反復射と余同語反復射を互いに交差・貫入させてよいと言っています。
- ループムービングは、ループはどこに移動してもよいと言っています。しかし、$`\cat{C}`$ がモノイド圏でないと、ループの移動先の概念がハッキリしません。とりあえず、「ループを消してもよい」の形で使うことにします。
- しかし、テンパリー/リーブ圏のケース(例えば「テンパリー/リーブ圏とカウフマンのスケイン関係式」)などを考える、ループを単純に消してよいかは疑問です。
- トレース付きモノイド圏からヤンキング公理を除いた圏はフィードバック付きモノイド圏〈monoidal category with feedback〉と呼ばれます。場合によってヤンキング公理は強すぎるかも知れません。
- 必要な法則〈公理〉を見逃している可能性もあります。
- $`\cat{M} = \cat{C}`$ のケースでは、両側テレオロジー圏は自己双対コンパクト閉圏とよく似た構造になります。テレオロジー圏とコンパクト閉圏には、親族的関連性があるのでしょう。
- テレオロジー圏では(入力と出力のあいだの)依存性を扱えません。双圏や二重圏を使って依存性を導入する手法があるので、その手法に沿ってテレオロジー圏/両側テレオロジー圏を拡張できるかも知れません(よく知らんけど)。
プレオートマトン
$`\cat{C} = (\cat{C}, \otimes , I, \sigma)`$ (記号の乱用、詳細省略)を対称モノイド圏とします。$`\cat{C}`$ は $`\cat{C}`$ 自身にモノイド作用するので、左アクテゴリーとみなします。左アクテゴリーとみなした $`\cat{C}`$ をベースとする両側テレオロジー圏を $`\cat{T}`$ とします。
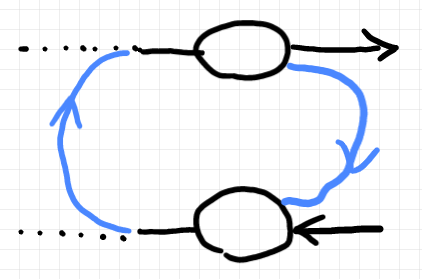
$`\cat{T}`$ のなかで次の4つの射を考えます。
- $`\eta^S_{[I, I]} : [I, I] \to [S\otimes I, S\otimes I] \In \cat{T}`$
- $`\J([\rho_S, \rho_S^{-1}]) : [S\otimes I, S\otimes I] \to [S, S]\In \cat{T}`$
- $`\J([f, f']): [S, S] \to [M\otimes A, M\otimes A'] \In \cat{T}`$
- $`\varepsilon^M_{[A, A']} : [M\otimes A, M\otimes A'] \to [A, A'] \In \cat{T}`$
これらを、この順で結合した射が($`\cat{T}`$ のなかの)基本プレオートマトン〈{basic | elementary} preautomaton〉です。これは、集合圏におけるプレオートマトン(オートマトンから初期状態を忘れた構造)に対応する $`\cat{T}`$ 内の構造です。
オートマトンの用語をそのまま使って、次のように呼びましょう。
- 対象 $`A \in |\cat{C}|`$ を出力アルファベット対象〈output alphabet object〉
- 対象 $`S \in |\cat{C}|`$ を状態空間対象〈state space object〉
- 対象 $`A' \in |\cat{C}|`$ を入力アルファベット対象〈input alphabet object〉
基本プレオートマトンの内部メカニズムを表現する射 $`\J([f, f']);\varepsilon^M_{[A, A']}`$ はオプティックの形をしています。圏 $`\cat{C}`$ がデカルト・モノイド圏ならば、レンズの形に書き換えることができます(「圏論的レンズ 訂正と補足: 具象レンズ=具象オプティック」参照)。
基本プレオートマトンに限らず、プロファイルが $`[I, I]\to [A, A']`$ である $`\cat{T}`$ の射を($`\cat{T}`$ のなかの)プレオートマトン〈preautomaton〉と呼びましょう。応用場面により、エージェント〈agent〉、ピボット〈pivot〉のような呼び名がふさわしいかも知れません。$`[I, I]\to [A, A']`$ は圏 $`\cat{T}`$ のポインティング射なので、対象 $`[A, A']`$ の“点”がプレオートマトンだとも言えます。
ミーリ-型とムーア型: 言い訳
状態遷移系/オートマトン/順序機械には、ミーリ-型〈Mealy-type〉とムーア型〈Moore-type〉があります。ミーリー型の遷移系は、状態遷移にともなって出力を行います。一方のムーア型の遷移系では、出力は遷移とは無関係で、状態に対して出力(観測値)が決まります。
事例としてミーリー型遷移系を扱ったのですが、僕が勘違いして、入力値〈入力ラベル〉と遷移後状態から出力値が決まる事例を作ってしまいました。通常、ミーリー型遷移系は入力値と遷移前状態から出力値が決まります。事例を作り直すのが面倒(絵もあるから)なので、以下ではそのままの事例を載せます。
事例を修正しなくてもそれほど問題ないだろう、という理由(言い訳ともいう)を述べておきます。まず、ミーリー型遷移系を次の3種に分けます。
- 一般ミーリー型遷移系: 出力値が、入力値、遷移の事前状態、事後状態により決定される。
- 事前ミーリー型遷移系: 出力値が、入力値、遷移の事前状態により決定される。
- 事後ミーリー型遷移系: 出力値が、入力値、遷移の事後状態により決定される。
通常のミーリー型遷移系は事前ミーリー型遷移系です。この記事で扱う事例は事後ミーリー型遷移系です。一般ミーリー型遷移系は両者を包摂します。
事前/事後のような時間的タイミングを調整するには、遷移系に履歴(過去の記憶)を持たせればいいので、次節で過去1回分の履歴を持つ遷移系〈プレオートマトン〉の作り方を説明します。
履歴付きプレオートマトン
圏 $`\cat{C}`$ はデカルト・モノイド圏だとして、$`\cat{C}`$ をベースとする両側テレオロジー圏 $`\cat{T}`$ において、以下のような簡単な基本プレオートマトンを考えましょう。
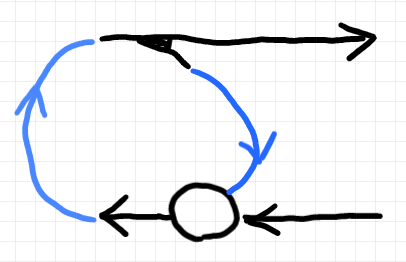
「簡単」と言いましたが、実は十分な一般性を持ちます。上段右側に観測射〈put射〉を結合すれば、レンズの形式になります。圏 $`\cat{C}`$ がデカルト圏なら、レンズとオプティックは同じことです(「圏論的レンズ 訂正と補足: 具象レンズ=具象オプティック」参照)。したがって、上の基本プレオートマトンは、レンズ/オプティックから作られるプレオートマトンの遷移部〈put射〉になっています。
与えられた基本プレオートマトンを、以下のように書き換えます。紫色のワイヤリングが、過去1回分の履歴を表現します。上段右側に結合される観測射は、紫色の過去の状態を(必要なら)参照することができます。
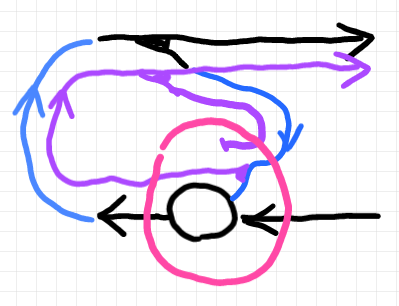
ピンクで囲った部分が新しい遷移部ですが、やっていることは元と変わりません。現状態(青)をコピーして履歴のワイヤーに流しています。新しい遷移部(ピンク) $`q`$ は、元の遷移部(黒) $`p`$ を使って次のように書けます。$`S`$ が状態空間、$`A'`$ が入力です。結合律子〈associator〉を使ったワイヤー操作は煩雑になるので省略しています。
$`\quad q := (\id_S \otimes \Delta_S \otimes \id_{A'}) ; (\pi^2_{S, S} ; p)`$
事後ミーリ-型からムーア型へ
引き続き圏 $`\cat{C}`$ はデカルト・モノイド圏だとして、$`\cat{C}`$ をベースとする両側テレオロジー圏 $`\cat{T}`$ 内の事後ミーリー型プレオートマトンとムーア型プレオートマトンを図示すると次のようになります。
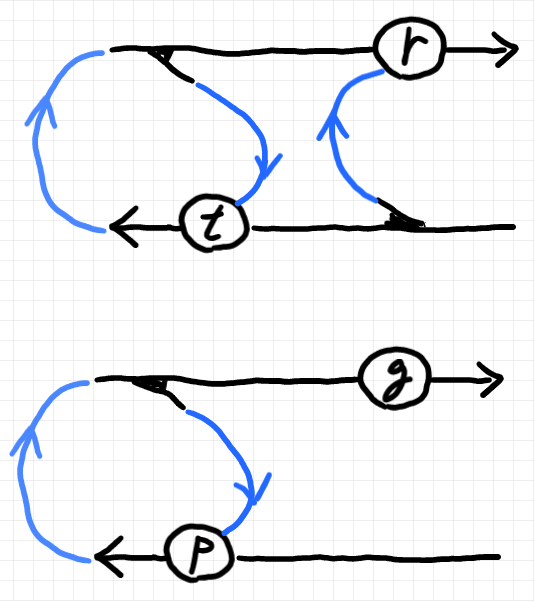
上のほうが事後ミーリー型で、$`r`$ がレスポンス射〈response morphism〉で $`t`$ が遷移射〈transition morphism〉です。下はムーア型ですが、これは余同語反復射付きのレンズと同じです。$`g`$ はget射〈get morphism〉、$`p`$ はput射〈put morphism〉です。
テキストで表記するのは面倒ですが、バラして書いてみます。事後ミーリー型プレオートマトンは以下の射の結合になります。1から3が左半分、4から6が右半分です。
- $`\eta^S_{[I, I]} : [I, I] \to [S\otimes I, S\otimes I]`$
- $`\J([\rho_{S}, \rho_{S}^{-1}]) : [S\otimes I, S\otimes I] \to [S, S]`$
- $`\J([\Delta_S, t]) : [S, S] \to [S\otimes S, S\otimes A']`$
- $`\varepsilon^S_{[S, A']} : [S\otimes S, S\otimes A'] \to [S, A']`$
- $`\eta^{A'}_{[S, A']} : [S, A'] \to [A'\otimes S, A'\otimes A']`$
- $`\J([r, \Delta_{A'}]) : [A'\otimes S, A'\otimes A'] \to [A, A']`$
そして、ムーア型プレオートマトンは以下の射の結合になります。
- $`\eta^S_{[I, I]} : [I, I] \to [S\otimes I, S\otimes I]`$
- $`\J([\rho_{S}, \rho_{S}^{-1}]) : [S\otimes I, S\otimes I] \to [S, S]`$
- $`\J(\Delta_S, p]) : [S, S] \to [S\otimes S, S\otimes A']`$
- $`\varepsilon^S_{[S, A']} : [S\otimes S, S\otimes A'] \to [S, A']`$
- $`\J([g, \id_{A'}]) : [S, A'] \to [A, A']`$
事後ミーリー型プレオートマトンは、ムーア型プレオートマトンでエミュレート出来ます。ストリング図で確認してみましょう。与えられた事後ミーリー型プレオートマトンのストリング図を変形して、ムーア型プレオートマトンのストリング図を構成します。新しくできたムーア型プレオートマトンの状態空間対象は $`A'\otimes S`$ になります。
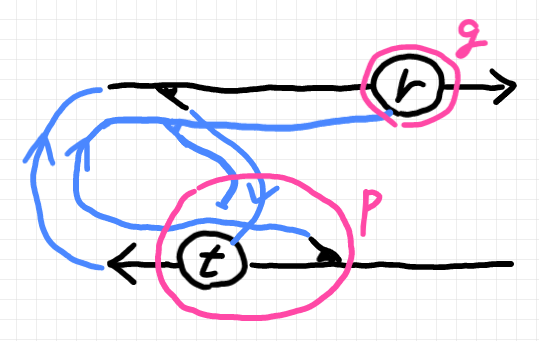
ムーア型プレオートマトンのget射とput射(ピンクで囲っている)は次のようです。
$`\quad g := r : A'\otimes S \to A \In \cat{C}\\
\quad p := (\pi^2_{A', S} \otimes \Delta_{A'} ); (\sigma_{S, A'}\otimes \id_{A'}); (\id_{A'} \otimes t) : (A'\otimes S)\otimes A' \to A'\otimes S \In \cat{C}
%`$
$`\cat{C}`$ が集合圏のときは、変数を使ってもっと具体的な表示が得られます。
事後ミーリー型プレオートマトンからムーア型プレオートマトンに変形する際に使われた法則〈変形規則〉は次のものです。
- オーバーラッピング
- 左タイトニング
- 右スライディング
他にデカルト・モノイド圏の法則は使っています。
「事後ミーリー型プレオートマトンは、ムーア型プレオートマトンでエミュレート出来る」ことは、集合圏では当たり前ですが、デカルト圏ベースの両側テレオロジー圏内でも同じ議論が通用することは、両側テレオロジー圏が意味を持ちそうな状況証拠と言えるでしょう。
*1:以前「ヘッジズ」と表記していましたが、「ジ」の後にアクセントがあるので、それを表すために「ヘッジーズ」にします。音を伸ばすというより、「ジ」を強く言います。