昨日、テレオロジー圏を拡張する話をしました。拡張した“両側テレオロジー圏”という概念に、どの程度の意義があるかハッキリとはわからないのですが、もとにしたテレオロジー圏という概念は、けっこう安定したものだろうと思います。そう思う理由は、テレオロジー圏の公理には、自然変換・対角自然変換として文字通り“自然な”解釈があるからです。
どうやらテレオロジー圏は、サイズランクも次元も高い世界に居る代数系のようです。テレオロジー圏がうまく扱えれば、大規模高次な代数系を扱う手法が見えてくるかも知れません。$`\newcommand{\cat}[1]{\mathcal{#1} }
\newcommand{\mrm}[1]{\mathrm{#1} }
\newcommand{\op}{\mathrm{op}}
\newcommand{\id}{\mathrm{id}}
\newcommand{\In}{\text{ in }}
\newcommand{\lact}{\mathop{\bullet} }
\newcommand{\J}{\mathrm{J} }
\newcommand{\twoto}{\Rightarrow}
\newcommand{\IXI} {\mathrm{I\!X\!I} }
\require{color}
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }%
\newcommand{\For}{\Keyword{For } }%
%`$
内容:
テレオロジー圏の公理
テレオロジー圏に対するセッティングは昨日の記事「両側テレオロジー圏とプレオートマトン」と同じとします。ただし、両側テレオロジー圏を作る気がないなら、モノイド圏 $`\cat{M}`$ の対称性はなくてもかまいません。出てくる素材は以下のものです。
- モノイド圏 $`\cat{M} = (\cat{M}, \otimes, I)`$ (対称とは限らない)
- 圏 $`\cat{C}`$
- 左モノイド作用 $`(\lact): \cat{M}\times \cat{C} \to \cat{C}`$
- 広い部分圏の包含関手 $`\J : \cat{C}\times \cat{C}^\op \to \cat{T}\: (|\cat{C}\times \cat{C}^\op| = |\cat{T}| )`$
- 同語反復射の族 $`\varepsilon^-_{[-, -]}`$
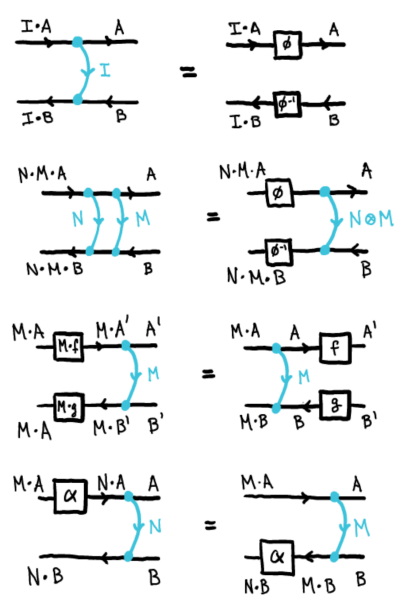
テレオロジー圏の公理とは、同語反復射の族に関する等式的法則です。昨日の記事でも引用しましたが、「圏論的レンズ 4: テレオロジー圏 // テレオロジー圏の定義」から図を再掲します。より詳しくは、もとの過去記事を読んでみてください。
同語反復射には次の4つの公理〈法則〉を要求します(ロマン論文 p.15 からコピー)。
図のなかのラベルがオーバーロードされて(同じ文字が違う意味で使われて)いてわかりにくいですね。3番目の等式の左辺下側のラベル $`M\lact A`$ は $`M\lact B`$ の間違いです。
トレース付きモノイド圏に倣って、4つの法則を次のように呼びます。
- バニシング〈Vanishing〉
- バンドリング〈Bundling〉
- タイトニング〈Tightening〉
- スライディング〈Sliding〉
左作用の拡張
左作用 $`(\lact)`$ を $`\cat{C}\times \cat{C}^\op`$ に拡張します。拡張した左作用の中置演算子記号は '$`\odot`$' とします。
$`\quad (\odot) = (- \odot [-, -]) : \cat{M}\times (\cat{C}\times \cat{C}^\op) \to (\cat{C}\times \cat{C}^\op) \In {\bf CAT}
%`$
$`(\odot)`$ の定義は次のようです。
$`\For M \in |\cat{M}|\\
\For [A, A'] \in |\cat{C}\times \cat{C}^\op|\\
\quad M \odot [A, A'] := [M\lact A, M\lact A'] \;\in |\cat{C}\times \cat{C}^\op|\\
\:\\
\For v: M \to X \In \cat{M}\\
\For [f, f']: [A, A'] \to [B, B'] \In \cat{C}\times \cat{C}^\op\\
\quad v \odot [f, f'] := [v\lact f, v\lact f'] \\
\quad : [ M\lact A, M\lact A'] \to [ X\lact A, X\lact A'] \In \cat{C}\times \cat{C}^\op\\
\text{i.e.}\\
\quad : M\odot [ A, A'] \to X \odot [ A, A'] \In \cat{C}\times \cat{C}^\op
%`$
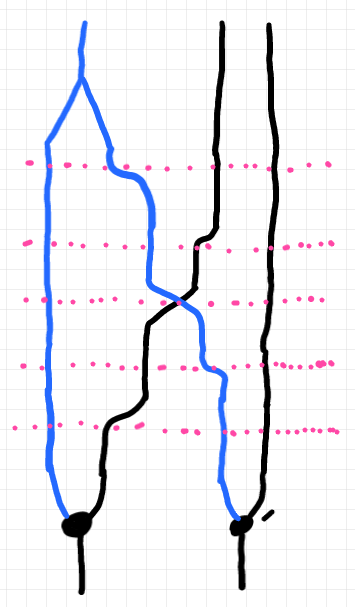
$`(\odot)`$ が双関手になることは確認する必要がありますが、それはルーチンワークです。$`(\odot)`$ の定義は、以下のように理解するといいでしょう。'$`*`$' は関手の図式順結合記号です。'$`\IXI`$' はひとつの記号文字だと思ってください(後述)。
$`\quad (\odot) := (\Delta_{\cat{M}} \times \mrm{Id}_{(\cat{C}\times \cat{C}^\op)}) *\IXI * ( (\lact) \times (\lact') )\\
\qquad : \cat{M}\times (\cat{C}\times \cat{C}^\op) \to(\cat{C}\times \cat{C}^\op)
\In {\bf CAT}
`$
ここで、$`(\lact')`$ は反対圏に働くモノイド作用、$`\IXI`$ は $`{\bf CAT}`$ の結合律子と対称〈スワップ〉のインスタンスの組み合わせです -- 象形文字のつもりですが、絵を描いたほうがハッキリしますね。以下の絵では、上から下が関手の結合方向(横結合が縦方向)、左から右が圏・関手の直積の方向です。ピンクの点線達が関手 $`\IXI`$ を構成します。$`\IXI`$ は、真ん中の二本のワイヤー($`\cat{M}`$ と $`\cat{C}`$)を入れ替える操作です。
この定義において、$`(\lact') : \cat{M}\times \cat{C}^\op \to \cat{C}^\op`$ が $`(\lact)`$ とは違った作用であることが注意点です。$`;'`$ を $`\cat{C}^\op`$ の結合だとして、例えば次のように計算します。$`(-)^\op`$ は、明示的に対象・射を反対圏のものだとみなすことを表します -- 通常は暗黙的にみなしが行われます。
$`\For M \in |\cat{M}|\\
\For f:A \to B, g: B\to C \In \cat{C}\\
\text{i.e.}\\
\For g: C\to B, f:B \to A \In \cat{C}^\op\\
\quad M \lact' (g \,;' f) : M\lact C \to M \lact A \In \cat{C}^\op \\
= (M \lact' g) \,;' (M \lact' f) : M\lact C \to M \lact A \In \cat{C}^\op \\
= \left( (M \lact f) ; (M \lact g): M\lact A \to M\lact C \In \cat{C} \right)^\op : M\lact C \to M \lact A\In \cat{C}^\op
%`$
射の向きはややこしいですねぇ。通常使われているストリング図表現では、$`\lact, \lact', \odot`$ の関係がうまく処理されるように工夫されています。
自然性としてのタイトニング
テレオロジー圏の $`\varepsilon^M_{[-, -]}`$ は次のような射の族になります。
$`\quad \varepsilon^M_{[-, -]} : \J(M\odot [-, -]) \to \J([-, -]) \In \cat{T}`$
以下の可換図式(を含む命題)が成立するなら、$`\varepsilon^M`$ は自然変換になります。
$`\require{AMScd}
\forall\, [f, f']: [A, A']\to [B, B'] \In \cat{C}\times \cat{C}^\op \,.\\
\quad \begin{CD}
\J(M \odot [A, A']) @>{\varepsilon^M_{[A, A']}}>> \J([A, A']) \\
@V{\J(\id_M \odot[f, f'])}VV @V{\J([f, f'])}VV\\
\J(M\odot [B, B']) @>{\varepsilon^M_{[B, B']}}>> \J([B, B']) \\
\end{CD}\\
\text{commutative in }\cat{T}
%`$
定義にしたがってストリング図を描いてみると、上の自然性の条件はタイトニング法則になっています。つまり、タイトニング法則は、$`\varepsilon^M`$ が次のような自然変換になることを主張しています。
$`\For M\in |\cat{M}|.\\
\quad \varepsilon^M :: \J(M\odot[-,-]) \twoto \J([-,-]) : \cat{C}\times \cat{C}^\op \to \cat{T} \In {\bf CAT}
%`$
この形を見ると、$`\varepsilon`$ は“総称自然変換”とでも呼ぶべき存在だと思えます。この事情をもう少しハッキリさせましょう。
記法を簡潔にするために、
$`\quad \cat{D} := \cat{C}\times\cat{C}^\op\\
\quad (M\odot) := (M\odot [-, -])
`$ とします。自然変換の集合は $`\mrm{Nat}(-, - : \cdots)`$ の形で書きます。'$`: \cdots`$' の部分は省略することもあります。
自然変換の集合達は、$`\cat{M}`$ の対象をインデックス〈パラメータ〉とするインデックス〈パラメータ〉付き集合族〈{indexed | parameterized} family of sets〉とみなせます。
$`\quad |\cat{M}| \ni M \mapsto \mrm{Nat}( (M\odot)* \J , \J : \cat{D}\to \cat{T}) \In {\bf SET}
%`$
この集合族に対して、依存型理論のパイ型を作ります(パイ構成)。パイ型は、シグマ型のセクションの集合でした。
$`\quad \prod_{M\in |\cat{M}| } \mrm{Nat}( (M\odot)* \J , \J)
= \mrm{Sect}\left(\sum_{M\in |\cat{M}| } \mrm{Nat}( (M\odot)* \J , \J) \overset{\pi}{\longrightarrow} |\cat{M}| \right)
%`$
テレオロジー圏の $`\varepsilon`$ はこのパイ型の要素になっています。
$`\quad \varepsilon \in \prod_{M\in |\cat{M}| } \mrm{Nat}( (M\odot)* \J , \J)
%`$
通常の総称関数〈多相関数〉は、関数集合族のパイ型の要素でしたから、自然変換集合族のパイ型の要素である $`\varepsilon`$ を総称自然変換と呼んでも悪くはないでしょう。総称パラメータ域は $`|\cat{M}|`$ です。
モノイド単位とバニシング
左モノイド作用に関する左単位律子〈left unitor〉を、モノイド積の左単位律子とオーバーロードして $`\lambda`$ で表します。
$`\quad \lambda :: (I\lact -) \twoto \mrm{Id}_{\cat{C}} : \cat{C} \to \cat{C} \In {\bf CAT}`$
より具体的な形は:
$`\For A \in |\cat{C}|\\
\quad \lambda_A : I\lact A \to A \In \cat{C}`$
左作用の左単位律子を使って次のような自然変換(ラムダの太字)を構成できます。
$`\quad \boldsymbol{\lambda} :: (I\odot [-,-]) \twoto [-, -] : \cat{C}\times \cat{C}^\op \to \cat{C}\times \cat{C}^\op \In {\bf CAT}`$
あるいは、
$`\quad \boldsymbol{\lambda} :: (I\odot [-,-]) \twoto \mrm{Id}_{\cat{C}\times \cat{C}^\op} : \cat{C}\times \cat{C}^\op \to \cat{C}\times \cat{C}^\op \In {\bf CAT}`$
その定義は:
$`\For [A, A'] \in |\cat{C}\times \cat{C}^\op |\\
\quad \boldsymbol{\lambda}_{[A, A']} := [\lambda_A, \lambda_{A'}^{-1}] \\
\quad : [I\lact A, I\lact A'] \to [A, A'] \In \cat{C}\times \cat{C}^\op \\
\text{i.e.}\\
\quad : (I\odot [ A, A']) \to [A, A'] \In \cat{C}\times \cat{C}^\op
`$
これが自然変換になることは容易に確認できます。
バニシング法則は、次の等式と同じです。自然変換の世界の等式だったのです。
$`\quad \varepsilon^I = \boldsymbol{\lambda} * \J \; :: J(I\odot [-, -]) \twoto \J([-, -]) : \cat{C}\times \cat{C}^\op \to \cat{T}\In {\bf CAT}`$
もっと簡潔に書くと:
$`\quad \varepsilon^I = \boldsymbol{\lambda}* \J \; :: (I\odot) * \J \twoto \J : \cat{D} \to \cat{T}\In {\bf CAT}`$
これを、圏の2-圏のストリング図として描くと次のようになります。この絵の縦方向は縦結合で、横方向は横結合です。
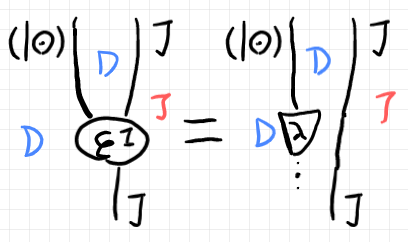
自然変換のあいだの等式は、圏の2-圏の3-射なので、3-射として書いてみると次のようです。
$`\quad \text{Vanishing} \\
\qquad ::: \varepsilon^I \equiv\!> \boldsymbol{\lambda} * \J \\
\qquad :: (I\odot) * \J \twoto \J \\
\qquad : \cat{D} \to \cat{T}\\
\quad \In {\bf CAT}`$
大規模高次な代数系を記述するには、構成素としての総称自然変換や、等式的法則としての3-射などが必要そうだと見当が付きます。
モノイド積とバンドリング
左モノイド作用に関する結合律子〈associator〉を、モノイド積の結合律子とオーバーロードして $`\alpha`$ で表します。
$`\For M, N\in |\cat{M}|\\
\quad \alpha^{M, N} :: ( (M\otimes N)\lact -) \twoto M\lact (N\lact - ) : \cat{C} \to \cat{C}
\In {\bf CAT}
%`$
より具体的な形は:
$`\For M, N\in |\cat{M}|\\
\For A\in |\cat{C}|\\
\quad \alpha^{M, N}_{A}: (M\otimes N)\lact A \to M\lact (N\lact A ) \In \cat{C}
%`$
左作用の結合律子を使って次のような自然変換の族(アルファの太字)を構成できます。
$`\For M, N\in |\cat{M}|\\
\quad \boldsymbol{\alpha}^{M, N} :: ( (M\otimes N)\odot) \twoto (N\odot) * (M\odot) : \cat{C}\times \cat{C}^\op \to \cat{C}\times \cat{C}^\op \In {\bf CAT}`$
ここで:
$`\quad ( (M\otimes N)\odot) : \cat{C}\times \cat{C}^\op \to \cat{C}\times \cat{C}^\op \In {\bf CAT}\\
\quad (N\odot) : \cat{C}\times \cat{C}^\op \to \cat{C}\times \cat{C}^\op \In {\bf CAT}\\
\quad (M\odot) : \cat{C}\times \cat{C}^\op \to \cat{C}\times \cat{C}^\op \In {\bf CAT}
`$
$`\boldsymbol{\alpha}^{M, N}`$ の定義は:
$`\For M, N\in |\cat{M}|\\
\For [A, A'] \in |\cat{C}\times \cat{C}^\op |\\
\quad \boldsymbol{\alpha}^{M,N}_{[A, A']} := [\alpha^{M,N}_A, {\alpha^{M,N}_{A'}}^{-1}] \\
\quad : [(M\otimes N)\lact A, (M\otimes N)\lact A'] \to
[ M\lact (N \lact A), M\lact ( N\lact A')] \In \cat{C}\times \cat{C}^\op
`$
バンドリング法則は次の等式を主張しています。すぐ後に圏の2-圏での絵も示します。
$`\For M, N\in |\cat{M}|\\
\quad \varepsilon^{M\otimes N} =
(\boldsymbol{\alpha}^{M,N} * J) ; ( (N\odot) * \varepsilon^M) ; \varepsilon^N \\
\qquad :: ( (M\otimes N) \odot ) * \J \twoto \J \\
\qquad : \cat{C}\times \cat{C}^\op \to \cat{T}\\
\quad \In {\bf CAT}
%`$
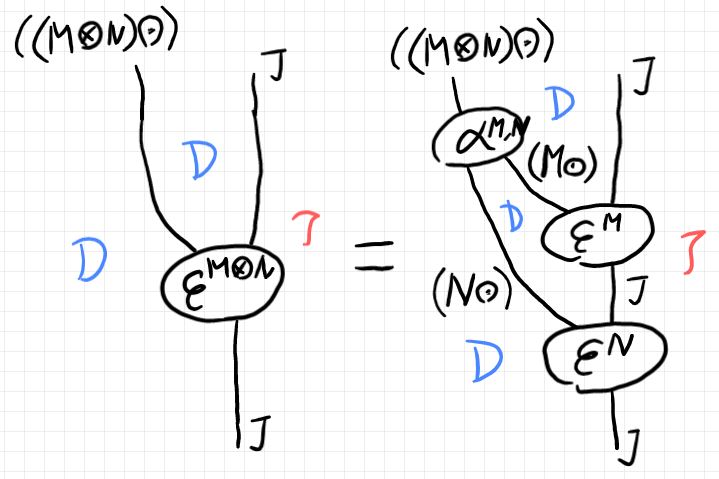
等式的法則を3-射として書いてみると次のようです。
$`\quad \text{Bundling}_{M, N} \\
\qquad ::: \varepsilon^{M\otimes N} \equiv\!> (\boldsymbol{\alpha}^{M,N} * J) ; ( (N\odot) * \varepsilon^M) ; \varepsilon^N \\
\qquad :: ( (M\otimes N) \odot ) *\J\twoto \J \\
\qquad : \cat{D} \to \cat{T}\\
\quad \In {\bf CAT}`$
バニシングとバンドリングを並べて書いてみると、大規模高次な指標〈signature〉な感じがします。
$`\quad \text{Vanishing} \\
\qquad ::: \varepsilon^I \equiv\!> \boldsymbol{\lambda} \\
\qquad :: (I\odot) * \J \twoto \J \\
\qquad : \cat{D} \to \cat{T}\\
\quad \In {\bf CAT}\\
\:\\
\For M, N\in |\cat{M}|\\
\quad \text{Bundling}_{M, N} \\
\qquad ::: \varepsilon^{M\otimes N} \equiv\!> (\boldsymbol{\alpha}^{M,N} * J) ; ( (N\odot) * \varepsilon^M) ; \varepsilon^N \\
\qquad :: ( (M\otimes N) \odot ) * \J \twoto \J \\
\qquad : \cat{D} \to \cat{T}\\
\quad \In {\bf CAT}`$
対角自然性としてのスライディング
$`[A, A'] \in |\cat{C}\times \cat{C}^\op|`$ に対して、$`\mrm{G}_{[A, A']}`$ という関手(反変・共変双関手)を定義します。既に約束したように、 $`\cat{D} := \cat{C}\times\cat{C}^\op`$ とします。
$`\quad \mrm{G}_{[A, A']} : \cat{M}\times \cat{M}^\op \to \cat{D} \In {\bf CAT}`$
$`\mrm{G}_{[A, A']}`$ の定義は次のとおり。$`\cat{M}\times \cat{M}^\op`$ の対象・要素もブラケットで囲ったペアで表します。
$`\For [M, N]\in |\cat{M}\times \cat{M}^\op|\\
\quad \mrm{G}_{[A, A']}([M, N]) := [M\lact A, N\lact A'] \;\in |\cat{D}|\\
\For [v, w] : [M, N] \to [X, Y] \In \cat{M}^\op\times \cat{M}\\
\quad \mrm{G}_{[A, A']}([v, w]) := [v\lact \id_A, w\lact \id_{A'}]\\
\quad : [M\lact A, N\lact A'] \to [X\lact A, Y\lact A'] \In \cat{D}\\
\text{i.e.}\\
\quad : \mrm{G}_{[A, A']}([M, N]) \to \mrm{G}_{[A, A']}([X, Y]) \In \cat{D}
`$
この $`\mrm{G}_{[A, A']}`$ をベースに考えると、テレオロジー圏の $`\varepsilon`$ は次のような族になります。
$`\quad \varepsilon^M_{[A, A']} : \J(\mrm{G}_{[A, A']}([M, M]) ) \to \J([A, A']) \In \cat{T}`$
形をそろえるために、$`\mrm{K}_{[A, A']}`$ を次のような関手とします。
$`\quad \mrm{K}_{[A, A']} : \cat{M}\times \cat{M}^\op \to \cat{D} \In {\bf CAT}\\
\;\\
\For [M, N]\in |\cat{M}\times \cat{M}^\op|\\
\quad \mrm{K}_{[A, A']}([M, N]) := [A, A'] \;\in |\cat{D}|\\
\For [v, w] : [M, N] \to [X, Y] \In \cat{M}^\op\times \cat{M}\\
\quad \mrm{K}_{[A, A']}([v, w]) := [\id_A, \id_{A'}]\\
\quad : \mrm{K}_{[A, A']}([M, N]) \to \mrm{K}_{[A, A']}([X, Y]) \In \cat{D}
`$
次の形に書き換えることができます。
$`\quad \varepsilon^M_{[A, A']} : \J(\mrm{G}_{[A, A']}([M, M]) ) \to \J(K_{[A, A']}([M, M]))
\In \cat{T}`$
$`M`$ を動かした全体が自然変換になるかというと、そうはなりません。が、対角自然変換になります。対角自然変換を、矢印 '$`\overset{\bullet}{\twoto}`$' で表すと:
$`\quad \varepsilon_{[A, A']} :: \mrm{G}_{[A, A']} * \J \overset{\bullet}{\twoto} K_{[A, A']} * \J : \cat{M}\times\cat{M}^\op \to \cat{D}`$
対角自然変換〈dinatural transformation〉の定義については、nLab項目 "dinatural transformation" などを参照してください。
以上のセッティングで、テレオロジー圏のスライディング法則は、$`\varepsilon_{[A, A']}`$ の対角自然性を主張しています。
上下の添字を持った $`\varepsilon^M_{[A, A']}`$ は上付き添字を固定して自然変換になり、下付き添字を固定して対角自然変換になります。そして、上付き添字はモノイド圏 $`\cat{M}`$ のモノイド積と協調します。
おわりに
まとめると、テレオロジー圏の $`\varepsilon^-_{[-, -]}`$ は次の性質を持ちます。
- 上付き添字を固定して自然変換
- 下付き添字を固定して対角自然変換
- 上付き添字はモノイド積と協調する
このような事実を、スッキリと短く書く記述方法はないものでしょうか? ロマン〈Mario Roman〉のストリング図は確かに便利ですが、大規模高次な代数系を直接的に表現する記法・描画法が欲しいところです。