昨日の記事「カリー vs. カン、双対 vs. 随伴」を使った事例として、表題の定理を示してみます。$`\newcommand{\mrm}[1]{ \mathrm{#1} }
\newcommand{\In}{\text{ in }}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\hyp}{\text{-} }
%\newcommand{\id}{\mathrm{id} }
\newcommand{\twoto}{\Rightarrow }
`$
内容:
セットアップ
「左随伴関手は左カン拡張を保存する。〈Left adjoint functors preserve left Kan extensions.〉」は、ペレスの次の論文の Proposition 1.6 として出てきます。もちろん、他でも目にすることはあるでしょう。
- [Per16-]
- Title: Coends and the tensor product of C-modules
- Author: Marco A. Pérez
- Submitted: 9 Aug 2016 (v1), 4 Oct 2016 (v3)
- Pages: 37p
- URL: https://arxiv.org/abs/1608.02828
$`(K, F, G, \alpha)`$ は左カン拡張を定義する構造だとします。$`\mrm{lun}`$ は左拡張実行2-射(「カリー vs. カン、双対 vs. 随伴」参照)です。
- $`\cat{C}, \cat{D}, \cat{E}`$ は圏(2-圏 $`{\bf Cat}`$ の対象)
- $`K:\cat{C} \to \cat{D} \In {\bf Cat}`$
- $`F:\cat{C} \to \cat{E} \In {\bf Cat}`$
- $`G := {_K F} = \mrm{Lan}_K F :\cat{D} \to \cat{E} \In {\bf Cat}`$
- $`\alpha := \mrm{lun} = \mrm{lun}_{K, F} :: F \twoto K * {_K F} : \cat{C} \to \cat{E} \In {\bf Cat}`$
この状況をストリング図で描けば次のようになります。オレンジ色は別名を付けたことを示します。
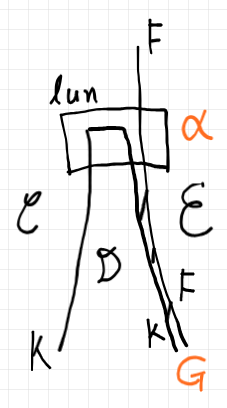
この構造から定義される左拡張カン化〈left extension Kanning〉を、象形文字 $`{_\vee \hyp}`$ で表します(ハイフンはプレースホルダー)。$`\beta \mapsto \mrm{lun} \,; (K * \beta)`$ で定義される反左拡張カン化〈left extension unKanning | 左拡張反カン化〉は、象形文字 $`{^\sqcap \hyp}`$ で表します。
$`P \dashv Q`$ は随伴系とします。
- $`P:\cat{E} \to \cat{F} \In {\bf Cat}`$
- $`Q:\cat{F} \to \cat{E} \In {\bf Cat}`$
- $`\eta :: \mrm{Id}_\cat{E} \twoto P*Q : \cat{E} \to \cat{E} \In {\bf Cat}`$
- $`\varepsilon:: Q*P \twoto \mrm{Id}_\cat{F} : \cat{F} \to \cat{F} \In {\bf Cat}`$
この状況をストリング図で描けば次のようになります。
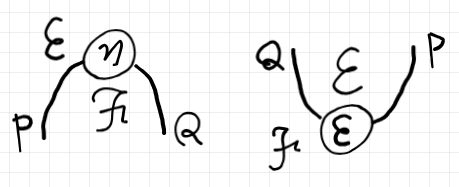
この随伴系から定義される、単位と余単位を結合するオペレータ〈コンビネータ〉を、象形文字 $`{\hyp ^\cap}, {\hyp _\cup}`$ で表します(「カリー vs. カン、双対 vs. 随伴」参照)。
一般に、関手 $`H:\cat{E} \to \cat{F}`$ が左カン拡張(の構造)$`(K, F, G, \alpha)`$ を保存する〈preserve〉とは、$`H`$ をポスト横結合した $`(K, F*H, G*H, \alpha*H)`$ が再び左カン拡張となることです。$`(K, F*H, G*H, \alpha*H)`$ が左カン拡張であることを示すには、新しい左拡張カン化 $`{_{\vee'} \hyp}`$ と反左拡張カン化 $`{^{\sqcap'} \hyp}`$ を定義して、互いに逆になることを確認すればOKです。
左拡張カン化の構成
もとの左拡張の構造に、随伴系の左関手である $`P`$ をポスト横結合した構造は次のようになります。$`F' := F*P`$、$`\mrm{lun'} := \mrm{lun}*P`$ と別名を付けています。
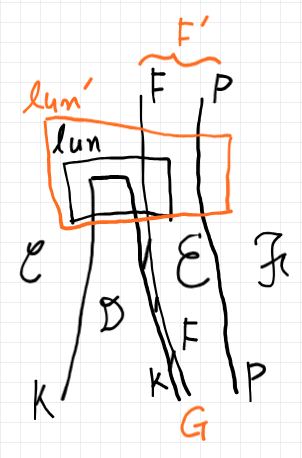
これが、カン(形容詞)とは限らない“$`K`$ に沿った左拡張”の構造を定義するのは確実です。形容詞としての「カン」は、「圏論的な普遍性を持つ」という意味です。
$`\quad \mrm{lun'} :: F' \twoto K*(G*P) : \cat{C} \to \cat{E} \In {\bf Cat}`$
上記の左拡張の構造がカンであるためには、次の形をした任意の2-射〈自然変換〉 $`\beta`$ に対して左拡張カン化が必要です。
$`\quad \beta :: F' \twoto K* G' :\cat{C} \to \cat{F} \In {\bf Cat}\\
\quad \text{where }\: F' = F*P
`$
必要とされる新しい左拡張カン化と、$`\mrm{lun'} = \mrm{lun} * P`$ から作られる新しい反左拡張カン化は次のようなものです。
$`\quad \mrm{Nat}(F', K* G') \ni \beta \mapsto {_{\vee'} \beta} \in \mrm{Nat}({_K F'}, G')\\
\quad \mrm{Nat}(G*P, G') \ni \gamma \mapsto {^{\sqcap'} \gamma} \in \mrm{Nat}(F', K*G')
`$
ここで、$`{_K F'}`$ も新しい左カン拡張で次のように定義されます。
$`\quad {_K F'} = {_K (F*P)} := ({_K F})*P`$
あるいは:
$`\quad \mrm{Lan'}_K F' = \mrm{Lan'}_K (F*P) := (\mrm{Lan}_K F)*P`$
さて、$`\beta \in \mrm{Nat}(F', K* G')`$ に対する新しい左拡張カン化 $`{_{\vee'} \beta}`$ は次のように定義します。
$`\quad {_{\vee'} \beta} := ({_\vee (\beta^\cap)})_\cup`$
$`{_\vee \hyp}`$ はもとの左拡張カン化、$`{\hyp^\cap}, {\hyp_\cup}`$ は随伴系から決まるオペレータです(「カリー vs. カン、双対 vs. 随伴」参照)。絵で描けば次のようです。
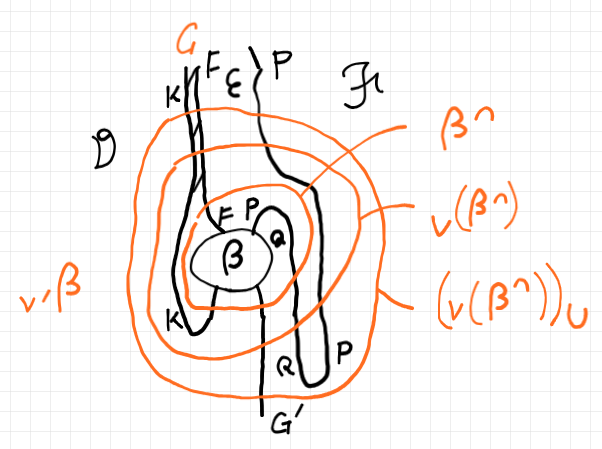
$`\gamma \in \mrm{Nat}(G*P, G')`$ に対する新しい反左拡張カン化の定義は次です。
$`\quad {^{\sqcap'} \gamma} := \mrm{lun'} \, ; (K* \gamma)\\
\quad \text{where }\: \mrm{lun'} := \mrm{lun} * P :: F' \twoto K*(G*P)
`$
これで、$`{_{\vee'} \hyp}, {^{\sqcap'} \hyp}`$ (それと、新しい左カン拡張 $`\mrm{Lan'}_K`$ も)定義できたので、次の等式が成立すれば目的は達成されます。
$`\quad {^{\sqcap'}({_{\vee'} \beta})} = \beta\\
\quad {_{\vee'}({^{\sqcap'} \gamma})} = \gamma
`$
あとは、定義に基づいて計算すればいいだけです。しかし、計算の途中のブックキーピング〈帳簿管理〉的作業が面倒です。ストリング図が助けになります。例えば $`{^{\sqcap'}({_{\vee'} \beta})}`$ の計算は、以下の図の上下のパーツをワイヤーで繋いで、それからワイヤーストレッチングを実行すればいいわけです。
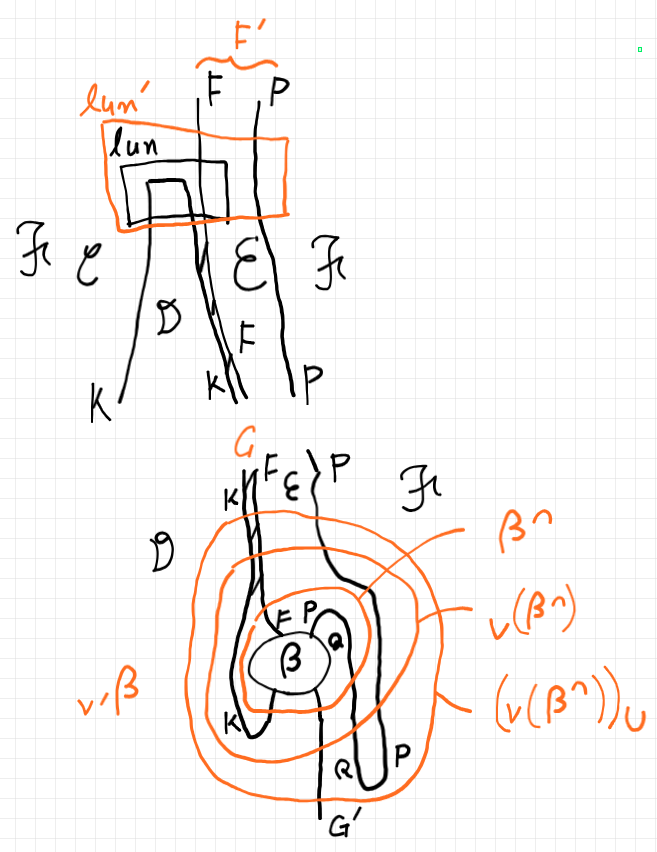
もとの左カン拡張の普遍性(ラムダ計算のベータ等式に相当)で $`K`$ のワイヤーがストレッチされ、随伴系のニョロニョロ等式で $`P, Q`$ のニョロニョロがストレッチされて $`\beta`$ だけが残るので、$`{^{\sqcap'}({_{\vee'} \beta})} = \beta`$ が示せます。$`{_{\vee'}({^{\sqcap'} \gamma})} = \gamma`$ もストリング図を眺めながら示せます。