カン拡張の左右について何度も書いています。
これだけ左右を話題にしていながら、今でも僕はカン拡張の左右で混乱します。これはいったい何なんだろう? と、もう一度考えてみました。
わかった! 混乱の原因はラムダ計算とのアナロジーだ。僕にとって、ラムダ計算は馴染み深いものです。なので、カン拡張を考える場合も(無意識に)ラムダ計算とのアナロジーを使ってしまいます。が、ラムダ計算の左右とカン拡張の左右では、用法が全然違うのです。「左右が逆」ならまだ補正が効くのですが、「左右が違った目的で使われる」ので戸惑ってしまうのです。
これは、言葉遣いの問題に過ぎません。が、言葉で引っかかると理解や思考が阻害されることがあります。そんなとき僕は、「悪さをする言霊のせいだ」と言ったり書いたりしていました。言霊恐ろしや。
- このブログ内の 言霊 の検索結果
この記事で、カン拡張とラムダ計算のアナロジーと、形容詞「左-右」がどう使われているかを説明します。$`\newcommand{\mrm}[1]{ \mathrm{#1} }
\newcommand{\In}{\text{ in }}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\hyp}{\text{-} }
\newcommand{\id}{\mathrm{id} }
\newcommand{\twoto}{\Rightarrow }
`$
内容:
二分法と形容詞
なにかを二種類に分類することや、分類の基準・手法を二分法〈dichotomy〉といいます。二つに分けられたモノ達のクラスをなんらかの形容詞を付けて呼びことが多いでしょう。二つのクラスを「左ナントカ」「右ナントカ」と呼び分けるなら、使用する形容詞も含めて左-右・二分法ということにします。左-右・二分法以外に、上-下・二分法、東-西・二分法、正-負・二文法なんかもあります。
「二分法」を拡張解釈して、モノが2つしかないときでも、それらを区別するときは二分法ということにします。随伴関手ペアを「左」と「右」で呼び分けるのは左-右・二分法です。ときに、片一方が形容詞なしのことがあります。「カリー化と反カリー化」とか「極限と余極限」とかは、片一方が形容詞なしです。こんなときは、形容詞なしのほうを「正」だとして、正-反・二分法とか正-余・二分法ということにします。
ラムダ計算を双対的ケースまで拡張すると、4つに分類できます。そのとき、左-右・二分法と正-余・二分法が使われます。例えば、指数対象〈exponential object〉は次のように呼び分けます。
| 左 | 右 | |
|---|---|---|
| 正 | 1. 左指数対象 | 2. 右指数対象 |
| 余 | 3. 左余指数対象 | 4. 右余指数対象 |
カン拡張も双対的ケースまで含めると、やはり4つに分類できます。そのとき、拡張-持ち上げ・二分法と左-右・二分法が使われます。
| 拡張 | 持ち上げ | |
|---|---|---|
| 右 | 1. 右カン拡張 | 2. 右カン持ち上げ |
| 左 | 3. 左カン拡張 | 4. 左カン持ち上げ |
ラムダ計算とカン拡張のアナロジーでは、同じ番号が付いた概念が対応します。
- 左指数対象 ←→ 右カン拡張
- 右指数対象 ←→ 右カン持ち上げ
- 左余指数対象 ←→ 左カン拡張
- 右余指数対象 ←→ 左カン持ち上げ
どちらか一方だけなら頑張っておぼえれば済みますが、両方を扱うと、二分法の基準が違うのでこんがらがってしまうのです。
言葉・呼び名をおぼえるのはやめて、できるだけ絵図と象形文字で理解することにします。この記事の最後に、絵図・象形文字と言葉・呼び名の対応表を示します。致し方ないから対応表は暗記することにして、理解や思考の手段に言葉・呼び名は使わないことにします。言霊が悪さするので。
そうは言っても、コミュニケーション手段として言葉・呼び名を使わざるを得ないので、この記事は言葉・呼び名を使って書いています。書いている僕は、カン拡張に関する拡張-持ち上げ・二分法と左-右・二分法は、完全に符丁〈識別ラベル〉だとして扱っています。
モノイド圏におけるラムダ計算
$`\cat{C} = (\cat{C}, \otimes, I)`$ (記号の乱用)を、対称とは限らないモノイド圏とします。$`\cat{C}`$ の特定の対象 $`T`$ に対して、$`T`$ を左から(モノイド積の意味で)掛け算する関手を次のように書きます。
$`\quad (T\otimes \hyp) = T^\otimes(\hyp) : \cat{C} \to \cat{C} \In {\bf CAT}`$
この関手を次のように呼びます。
- $`T`$ による左掛け算関手〈left multiplication functor〉
- $`T`$ による左テンソリング関手〈left tensoring functor〉
- $`T`$ による左{モノイド}?スタンピング関手〈left {monoidal}? stamping functor〉
$`T`$ による左掛け算関手の右随伴関手を、$`T`$ による左指数関手〈left exponential functor〉と呼びます。左指数関手の値である対象を左指数対象〈left exponential object〉と呼びます。「指数」と「内部ホム〈internal hom〉」は完全に同義語として使います。したがって:
- 左指数関手 = 左内部ホム関手〈left internal hom functor〉
- 左指数対象 = 左内部ホム対象〈left internal hom object〉
左指数対象=左内部ホム対象を次のように書きます。
$`\quad {^T A} = \mrm{lhom}(T, A) \;\in |\cat{C}|`$
型理論やプログラミング言語では、左(または右)指数対象を矢印 $`\to`$ を使って表しますが、圏論の文脈で矢印を使うと混乱のもとなので、斜め矢印にします。
$`\quad T\searrow A = {^T A} = \mrm{lhom}(T, A) \;\in |\cat{C}|`$
$`T`$ による左指数関手は次のように書けます。
$`\quad (T\searrow \hyp) = {^T \hyp} = \mrm{lhom}(T, \hyp) : \cat{C}\to\cat{C}\In {\bf CAT}`$
以上の定義から、次のような、随伴ペアに伴うホムセット同型が成立します。
$`\quad \cat{C}(T^\otimes(B), A) \cong \cat{C}(B, \mrm{lhom}(T, A)) \;\In {\bf Set}`$
別な記法を使っても、内容は何も変わりません。
$`\quad \cat{C}(T \otimes B, A) \cong \cat{C}(B, {^T A}) \;\In {\bf Set}\\
\quad \cat{C}(T \otimes B, A) \cong \cat{C}(B, T\searrow A) \;\In {\bf Set}
`$
このホムセット同型を与える写像(左カリー化コンビネータ〈left currying combinator〉)を $`{^\cap \hyp}`$ と書きます。この記法は、絵図を模した象形文字です。対応する絵図は次節で説明します。
$`\quad {^\cap \hyp} : \cat{C}(T \otimes B, A) \to \cat{C}(B, {^T A}) \;\In {\bf Set}
`$
左カリー化コンビネータを名前で書くなら、次のようになります。
$`\quad \mrm{LCurry}_{T, B, A} : \cat{C}(T \otimes B, A) \to \cat{C}(B, {^T A}) \;\In {\bf Set}
`$
左カリー化コンビネータの逆写像は左反カリー化コンビネータ〈left uncurrying combinator〉で、象形文字で次のように書きます。
$`\quad {_\sqcup \hyp} : \cat{C}(B, {^T A}) \to \cat{C}(T \otimes B, A) \;\In {\bf Set}
`$
左反カリー化は今まで $`{_\cup \hyp}`$ と書いてましたが、8種類のカリー化(後述)を考えるときは具合が悪いので、反カリー化は角ばった記号を使います。
左カリー化と左反カリー化は互いに逆なので次が成立します。
$`\text{For } f \in \cat{C}(T\otimes B, A)\\
\quad {_\sqcup {^\cap f}} = f \\
\text{For } g \in \cat{C}(B, {^T A} )\\
\quad {^\cap {_\sqcup g}} = g
`$
これはラムダ計算の基本公式であるベータ等式とイータ等式〈エータ等式〉です。
左反カリー化 $`{_\sqcup \hyp}`$ は、左評価射〈left evaluation morphism〉 $`\mrm{lev}`$ により、次のように書けます。
$`\mrm{lev}_{T, A} : T\otimes {^T A} \to A \In \cat{C}\\
\text{For } g \in \cat{C}(B, {^T A} )\\
\quad {_\sqcup g} = \mrm{LUncurry}_{T, B, A}(g) := (\id_T \otimes g) ; \mrm{lev}_{T, A}
\; : T\otimes B \to A \In \cat{C}
`$
ラムダ計算の絵図
「右カン拡張の eval は run」や「カン拡張における上下左右: 入門の前に整理すべきこと」に、ラムダ計算とカン拡張を対応させた絵図(ストリング図)が載っています。ここでは、新しく導入した $`{_\sqcup \hyp}`$ が象形文字となるように、評価射を四角で描く描画法を紹介します。この描画法でベータ等式とイータ等式を描いてみます。
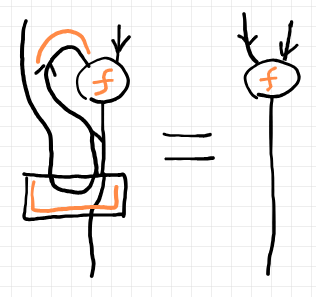
上図はベータ等式です。丸いキャップ $`\cap`$ がラムダ抽象〈カリー化〉を表します。角ばったカップ $`\sqcup`$ は評価射をポスト結合することを表します。なので、上の絵図等式は $`{_\sqcup{^\cap f}} = f`$ を表します。
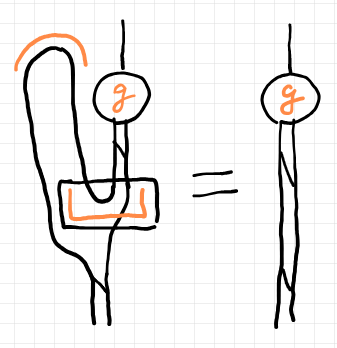
上図はイータ等式です。角ばったカップと丸いキャップの意味は同じです。上の絵図等式は $`{^\cap {_\sqcup g }} = g`$ を表します。
双対的なラムダ計算
前々節と同じ設定で話を続けます。
$`T`$ による左掛け算関手の左随伴関手を、$`T`$ による左余指数関手〈left coexponential functor〉と呼びます。左余指数関手の値である対象を左余指数対象〈left coexponential object〉と呼びます。「余指数」と「内部コホム〈internal cohom〉」は完全に同義語として使います。したがって:
- 左余指数関手 = 左内部コホム関手〈left internal cohom functor〉
- 左余指数対象 = 左内部コホム対象〈left internal cohom object〉
左余指数対象=左内部コホム対象を次のように書きます。
$`\quad {_T A} = \mrm{lcohom}(T, A) \;\in |\cat{C}|`$
次の斜め矢印も使います。斜め矢印の向きに何か意味があるわけではなくて、4種類の指数〈exponential〉を区別するために違う矢印を使っているだけです。
$`\quad T\nearrow A = {_T A} = \mrm{lcohom}(T, A) \;\in |\cat{C}|`$
$`T`$ による左余指数関手は次のように書けます。
$`\quad (T \nearrow \hyp ) = {_T \hyp} = \mrm{lcohom}(T, \hyp) : \cat{C}\to\cat{C}\In {\bf CAT}`$
以上の定義から、次のような、随伴ペアに伴うホムセット同型が成立します。
$`\quad \cat{C}(\mrm{lcohom}(T, A), B) \cong \cat{C}(A, T\otimes B) \;\In {\bf Set}`$
別な記法を使っても、内容は何も変わりません。
$`\quad \cat{C}( {_T A}, B) \cong \cat{C}(A, T\otimes B) \;\In {\bf Set}\\
\quad \cat{C}(T \nearrow A, B) \cong \cat{C}(A, T\otimes A) \;\In {\bf Set}
`$
このホムセット同型を与える写像(左余カリー化コンビネータ〈left cocurrying combinator〉)を $`{_\cup \hyp}`$ と書きます。この記法も象形文字です。
$`\quad {_\cup \hyp} : \cat{C}(A, T \otimes B) \to \cat{C}({_T, A}, B) \;\In {\bf Set}
`$
左余カリー化コンビネータを名前で書くなら、次のようになります。
$`\quad \mrm{LCocurry}_{A, T, B} : \cat{C}(A, T \otimes B) \to \cat{C}({_T A}, B) \;\In {\bf Set}
`$
左余カリー化コンビネータの逆写像は左反余カリー化コンビネータ〈left uncocurrying combinator〉で、象形文字で次のように書きます。
$`\quad {^\sqcap \hyp} : \cat{C}({_T A}, B) \to \cat{C}(A , T \otimes B) \;\In {\bf Set}
`$
左余カリー化と左反余カリー化は互いに逆なので次が成立します。
$`\text{For } f \in \cat{C}(A, T\otimes B)\\
\quad {^\sqcap {_\cup f}} = f \\
\text{For } g \in \cat{C}({_T A}, B )\\
\quad {_\cup {^\sqcap g}} = g
`$
これは余ベータ等式と余イータ等式〈余エータ等式〉と呼んでいいでしょう。
左反余カリー化 $`{^\sqcap \hyp}`$ は、左余評価射〈left coevaluation morphism〉 $`\mrm{lcoev}`$ により、次のように書けます。
$`\mrm{lcoev}_{A,T} : A \to T \otimes {_T A} \In \cat{C}\\
\text{For } g \in \cat{C}({_T A}, B )\\
\quad {^\sqcap g} = \mrm{LUncocurry}_{A, T, B}(g) := \mrm{lcoev}_{A, T} ; (\id_T \otimes g)
\; : A \to T\otimes B \In \cat{C}
`$
右の場合
左掛け算関手の左を右にした $`(\hyp \otimes T) = T_\otimes(\hyp)`$ は、次のように呼びます。
- $`T`$ による右掛け算関手〈right multiplication functor〉
- $`T`$ による右テンソリング関手〈right tensoring functor〉
- $`T`$ による右{モノイド}?スタンピング関手〈right {monoidal}? stamping functor〉
これに基づいて、次の概念・用語・記法を定義できます。
- 右指数関手〈right exponential functor〉
- 右指数対象〈right exponential object〉
- 右内部ホム関手〈right internal hom functor〉
- 右内部ホム対象〈right internal hom object〉
- $`A^T = \mrm{rhom}(A, T)`$
- $`A \swarrow T = \mrm{rhom}(A, T)`$
- 右カリー化コンビネータ〈right currying combinator〉
- $`\hyp^\cap`$
- $`\mrm{RCurry}_{B, T, A} : \cat{C}(B\otimes T, A) \to \cat{C}(B, A^T)\In {\bf Set}`$
- 右反カリー化コンビネータ〈right uncurrying combinator〉
- $`{\hyp_\sqcup}`$
- $`{f^\cap}_\sqcup = f`$ (右ベータ等式)
- $`{g_\sqcup}^\cap = g`$ (右イータ等式〈右エータ等式〉)
- 右評価射〈right evaluation morphism〉
- $`\mrm{rev}_{A, T} : A^T \otimes T \to A \In \cat{C}`$
右掛け算関手の左随伴関手である右余指数関手を考えると、次の概念・用語・記法を定義できます。
- 右余指数関手〈right coexponential functor〉
- 右余指数対象〈right coexponential object〉
- 右内部コホム関手〈right internal cohom functor〉
- 右内部コホム対象〈right internal cohom object〉
- $`A_T = \mrm{rcohom}(A, T)`$
- $`A \nwarrow T = \mrm{rcohom}(A, T)`$
- 右余カリー化コンビネータ〈right cocurrying combinator〉
- $`\hyp_\cap`$
- $`\mrm{RCocurry}_{A, B, T} : \cat{C}(A, B\otimes T) \to \cat{C}(A_T, B)\In {\bf Set}`$
- 右反余カリー化コンビネータ〈right uncocurrying combinator〉
- $`{\hyp^\sqcup}`$
- $`{f_\cup}^\sqcap = f`$ (右余ベータ等式)
- $`{g^\sqcap}_\cup = g`$ (右余イータ等式〈右余エータ等式〉)
- 右余評価射〈right coevaluation morphism〉
- $`\mrm{rcoev}_{A, T} : A \to A_T \otimes T \In \cat{C}`$
ラムダ計算の中心的概念であるカリー化には、左-右・二分法、正-反・二分法、正-余・二分法が適用されるので、$`2^3 = 8`$ 種類のカリー化があります。これらを、添字の位置として、左上、右上、左下、右下、記号の形として丸っこい・角ばった記号で区別しています。
- 左-正-正 カリー化: $`{^\cap \hyp}`$
- 左-反-正 カリー化: $`{_\sqcup \hyp}`$
- 左-正-余 カリー化: $`{_\cup \hyp}`$
- 左-反-余 カリー化: $`{^\sqcap \hyp}`$
- 右-正-正 カリー化: $`{\hyp^\cap}`$
- 右-反-正 カリー化: $`{\hyp_\sqcup}`$
- 右-正-余 カリー化: $`{\hyp_\cup}`$
- 右-反-余 カリー化: $`{\hyp^\sqcap}`$
関手圏における右カン拡張
モノイド圏の代わりに圏達の2-圏やホム圏〈関手圏〉で考えます。関手圏は圏になりますが、そのホムセットは自然変換の集合です。自然変換の集合を $`\mrm{Nat}(\hyp, \hyp)`$ と書きます。ただし、$`\mrm{Nat}`$ は単一特定の関手圏ホムセットを表すのではなくて、出現する幾つかの関手圏のホムセットのためにオーバーロードされる名前です。関手と自然変換の横結合の図式順演算子記号に $`*`$ を使います。演算子記号 $`*`$ の左側からプレ結合し、右側からポスト結合することになります。
先のモノイド圏のセッティングと、圏達の2-圏/関手圏でのセッティングで、次のような対応があります。
| $`{\bf モノイド圏}`$ | $`{\bf 圏達の}\text{2-}{\bf 圏/関手圏}`$ |
|---|---|
| $`対象\: T`$ | $`関手\: K:\cat{C} \to \cat{D}`$ |
| $`対象\: A`$ | $`関手\: F:\cat{C} \to \cat{E}`$ |
| $`対象\: B`$ | $`関手\: G:\cat{D} \to \cat{E}`$ |
| $`射\: f:T\otimes B \to A`$ | $`自然変換\: \alpha :: K * G \twoto F`$ |
| $`射\: g: B\to \mrm{lhom}(T, A)`$ | $`自然変換\: \beta :: G \twoto \mrm{Ran}_K F`$ |
もう一度注意しておくと、ラムダ計算の左-右・二分法が、カン拡張の拡張-持ち上げ・二分法になり、ラムダ計算の正-余・二分法が、カン拡張の右-左・二分法になります。したがって、ラムダ計算の左指数対象の話が右カン拡張の話に対応します。
| $`{\bf ラムダ計算}`$ | $`{\bf カン拡張}`$ |
|---|---|
| $`\mrm{lhom}(T, A)`$ | $`\mrm{Ran}_K F`$ |
| $`\mrm{rhom}(A, T)`$ | $`\mrm{Rift}_K F`$ |
| $`\mrm{lcohom}(T, A)`$ | $`\mrm{Lan}_K F`$ |
| $`\mrm{rcohom}(A, T)`$ | $`\mrm{Lift}_K F`$ |
関手圏の特定の対象(つまり関手) $`K`$ に対して、$`K`$ を左から結合〈プレ結合〉する関手を次のように書きます。
$`\quad (K * \hyp) = K^*(\hyp) : \cat{C} \to \cat{C} \In {\bf CAT}`$
この関手を次のように呼びます。形容詞「左」は記法や図法に影響されます。
- $`K`$ による左結合メタ関手〈left composition metafunctor〉
- $`K`$ によるプレ結合メタ関手〈pre-composition metafunctor〉
- $`K`$ による引き戻しメタ関手〈pullback metafunctor〉
一時的な言い方ですが、関手圏のあいだの関手を“メタ関手”と呼ぶことにします。関手を引数に受け取って関手を返す関手がメタ関手です。
$`K`$ によるプレ結合メタ関手の右随伴関手を、$`K`$ に沿った右カン拡張メタ関手〈right Kan extension metafunctor〉と呼びます。右カン拡張メタ関手の値である関手を右カン拡張〈right Kan extension〉と呼びます。
右カン拡張を次のように書きます。
$`\quad {^K F} = \mrm{Ran}_K F \;\in | [\cat{C}, \cat{E}] |`$
$`K`$ に沿った右カン拡張メタ関手は次のように書けます。
$`\quad {^K \hyp} = \mrm{Ran}_K \hyp : [\cat{C}, \cat{E}] \to [\cat{D}, \cat{E}] \In {\bf CAT}`$
以上の定義から、次のような、随伴ペアに伴うホムセット同型が成立します。
$`\quad \mrm{Nat}(K^*(G), F) \cong \mrm{Nat}(G, \mrm{Ran}_K F) \;\In {\bf Set}`$
別な記法を使っても、内容は何も変わりません。
$`\quad \mrm{Nat}(K * G, F) \cong \mrm{Nat}(G, {^K F}) \;\In {\bf Set}\\
\quad [\cat{C},\cat{E} ](K * G, F) \cong [\cat{D}, \cat{E}](G, \mrm{Ran}_K F) \;\In {\bf Set}
`$
このホムセット同型を与える写像に広く合意された名前はないようですが $`{^\cap \hyp}`$ と書きます。この記法は、ラムダ計算の場合と同様に絵図〈ストリング図〉を模したものです。
$`\quad {^\cap \hyp} : \mrm{Nat}(K * G, F) \to \mrm{Nat}(G, {^K F}) \;\In {\bf Set}
`$
$`{^\cap \hyp}`$ の逆写像は、象形文字で次のように書きます。
$`\quad {_\sqcup \hyp} : \mrm{Nat}(G, {^K F}) \to \mrm{Nat}(K * G, F) \;\In {\bf Set}
`$
$`{^\cap \hyp}`$ と $`{_\sqcup \hyp}`$ は互いに逆なので次が成立します。
$`\text{For } \alpha \in \mrm{Nat}(K * G, F)\\
\quad {_\sqcup {^\cap \alpha}} = \alpha \\
\text{For } \beta \in \mrm{Nat}(G, {^K F} )\\
\quad {^\cap {_\sqcup \beta}} = \beta
`$
これは右カン拡張のベータ等式とイータ等式〈エータ等式〉と呼んでもいいでしょう。
写像 $`{_\sqcup \hyp}`$ は、右実行自然変換〈right execution natural transformation〉 $`\mrm{run}`$ により、次のように書けます(「右カン拡張の eval は run」参照)。
$`\mrm{run}_{K, F} : K * {^K F} \twoto F \In {\bf CAT}\\
\text{For } \beta \in \mrm{Nat}(G, {^K F} )\\
\quad {_\sqcup \beta} := (\mrm{ID}_K * \beta) ; \mrm{run}_{K, F}
\; :: K * G \twoto F \In {\bf CAT}
`$
その他の場合
図と共に、ラムダ計算の左-右・二分法と正・余・二分法を青で書き、カン拡張の拡張-持ち上げ・二分法と右・左・二分法を赤で書きます。ラムダ計算の Left-, Right- と、カン拡張の Right-, Left- はこのような対応関係になります。なるほどややこしい。
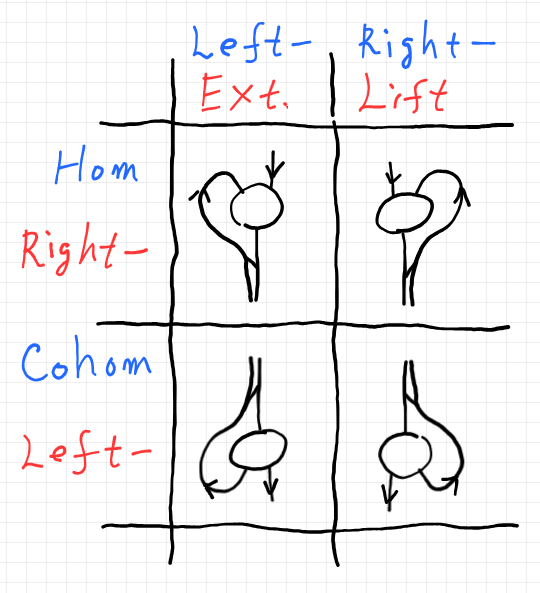
目ぼしい記号の対応は以下のようになります。
| $`{\bf ラムダ計算}`$ | $`{\bf カン拡張}`$ | $`{\bf 別記法}`$ |
|---|---|---|
| $`T^\otimes`$ | $`K^*`$ | |
| $`\mrm{lhom}(T, A)`$ | $`\mrm{Ran}_K F`$ | $`{^T A},\; T\searrow A`$ |
| $`{^\cap \hyp}`$ | $`{^\cap \hyp}`$ | |
| $`\mrm{lev}_{T, A}`$ | $`\mrm{run}_{K, F}`$ | |
| $`T_\otimes`$ | $`K_*`$ | |
| $`\mrm{lcohom}(T, A)`$ | $`\mrm{Lan}_K F`$ | $`{_T A},\; T\nearrow A`$ |
| $`{^\cup \hyp}`$ | $`{^\cup \hyp}`$ | |
| $`\mrm{lcoev}_{T, A}`$ | $`\mrm{lun}_{K, F}`$ | |
| $`\mrm{rhom}(A, T)`$ | $`\mrm{Rift}_K F`$ | $`{A^T},\; A \swarrow T`$ |
| $`{\hyp^\cap}`$ | $`{\hyp^\cap}`$ | |
| $`\mrm{rev}_{A, T}`$ | $`未定`$ | |
| $`\mrm{rcohom}(A, T)`$ | $`\mrm{Lift}_K F`$ | $`{A_T},\; A\nwarrow T`$ |
| $`{\hyp_\cup}`$ | $`{\hyp_\cup}`$ | |
| $`\mrm{rcoev}_{A, T}`$ | $`未定`$ |