「左加群は前層、右加群は余前層、双加群はプロ関手」で述べた事を敷衍して、左状態遷移系は前層、右状態遷移系は余前層、双状態遷移系はプロ関手であることを述べます。前層・余前層・プロ関手を、状態遷移系としても解釈できることになります。$`\newcommand{\mrm}[1]{ \mathrm{#1} }
\newcommand{\In}{\text{ in }}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\hyp}{\text{-} }
\newcommand{\id}{\mathrm{id} }
\newcommand{\twoto}{\Rightarrow }
\newcommand{\op}{\mathrm{op} }
\newcommand{\o}[1]{\overline{#1} }
\newcommand{\u}[1]{\underline{#1} }
\newcommand{\For}{\text{For } }
\newcommand{\Imp}{\Rightarrow }
\newcommand{\lact}{\triangleright }
\newcommand{\ract}{\triangleleft }
`$
内容:
捻じれ対のテキスト表示と図示
この節では、後で使う(たぶん、この記事以外からも参照する)記法と図法を準備します。
$`\cat{C}, \cat{D}`$ が圏のとき、$`\cat{C}^\op \times \cat{D}`$ や $`\cat{C}\times \cat{D}^\op`$ の射を、射の捻じれ対〈ねじれつい | twisted pair of morphisms〉と呼ぶことにします。
捻じれ対は色々な場面で登場しますが、図/テキストで表現するのが案外大変です。次のような情報を考えてみます。
- $`f: a \to b \In \cat{C}`$
- $`g: c \to d \In \cat{D}`$
$`f`$ を $`\cat{C}^\op`$ の射とみなしたものを第一成分、$`g`$ そのものを第ニ成分とする捻じれ対($`\cat{C}^\op \times \cat{D}`$ の射)をどう表したらいいでしょうか?
$`(f, g)`$ では $`\cat{C}\times \cat{D}`$ の射(通常の対)と区別がつきません。「反対圏/反変関手と、2-圏のストリング図 // 反対圏の対象と射のテキスト表示」で次のように書きました。
定義上は、$`\cat{C}`$ の対象・射と $`\cat{C}^\op`$ の対象・射はまったく同じです。
- $`\mrm{Obj}(\cat{C}) = \mrm{Obj}(\cat{C}^\op)`$
- $`\mrm{Mor}(\cat{C}) = \mrm{Mor}(\cat{C}^\op)`$
したがって、$`A\in |\cat{C}|`$ なら $`A\in |\cat{C}^\op|`$ です。しかし、注釈情報を添える意味で次の記法を使ってもいいでしょう。
- $`\cat{C}^\op`$ の対象としての $`A\in \mrm{Obj}(\cat{C}) = \mrm{Obj}(\cat{C}^\op)`$ は $`A^\uparrow`$ と書く。
- $`\cat{C}^\op`$ の射としての $`f\in \mrm{Mor}(\cat{C}) = \mrm{Mor}(\cat{C}^\op)`$ は $`f^\uparrow`$ と書く。
上向き矢印は注釈情報なので、なくてもいいし、取り去っても何も変わりません。それでも、反対圏や反変関手につきまとう混乱を避ける効果はあります。
反対圏の対象・射には、右肩に上向き矢印を添えるという記法です。印は何でもいいので、(上向き矢印ではなくて)上線〈overline〉を使うことにします。最近眺めた論文(タイトルは失念しました*1)で上線が使ってあって、具合が良さそうだったからです。
反対圏の射には上線を引く記法だと、先の情報は次のように書けます。
- $`f: a \to b \In \cat{C}`$
- $`\o{f}: \o{b} \to \o{a} \In \cat{C}^\op`$
- $`g: c \to d \In \cat{D}`$
- $`\o{g}: \o{d} \to \o{c} \In \cat{D}^\op`$
$`\cat{C}^\op \times \cat{D}`$ の射である捻じれ対は $`(\o{f}, g)`$ と書けます。ここで、$`f\in\mrm{Mor}(\cat{C})`$ 、 $`g\in \mrm{Mor}(\cat{D})`$ です。
次に捻じれ対の図示を考えます。まず、絵を描く2次元キャンバスに、描画方向として「射の順方向」と「ペアリング方向」を決めておきます。例えば、「射の順方向は上から下、ペアリング方向は左から右」のように。そして、次の約束をします。
- 射の捻じれ対 $`(\o{f}, g)`$ の $`\o{f}`$ は順方向と逆向きに(逆方向に)描く。
- 射の捻じれ対 $`(\o{f}, g)`$ の $`g`$ は順方向に描く。
- ペアリング方向に沿って、$`\o{f}`$ を最初に、$`g`$ を二番目に描く。
次は、捻じれ対 $`(\o{f}, g)`$ の図示の一例です。ドット&アロー図〈dots-and-arrows diagram〉とストリング図のハイブリッドで描いています。
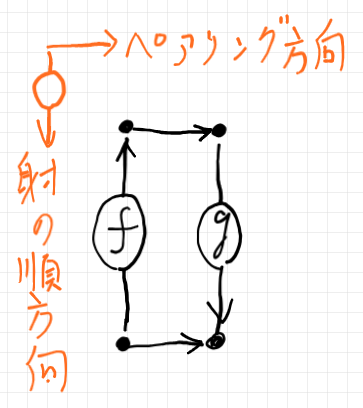
図では、反対圏の射は順方向と逆向きに(逆方向に)描くので上線を付けていません。しかし、描画方向が曖昧なときはラベルに上線を引いたほうが無難でしょう。対象のペアにもペアリング方向の矢印を描いています。ペアリング方向が明らかなときは矢印を省略してもかまいません。
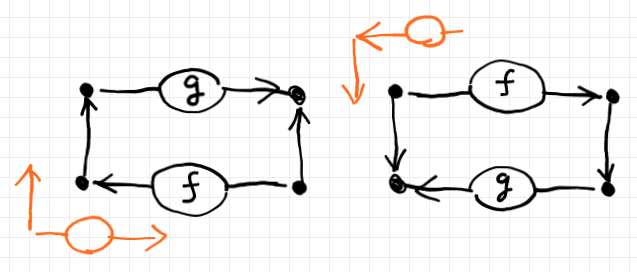
キャンバスの「射の順方向」と「ペアリング方向」はその場その場の約束で決めることにします。違った描画方向にすると、印象が変わるので注意してください。以下の左側は「順方向が左から右、ペアリング方向が下から上」で、右側は「順方向が右から左、ペアリング方向が上から下」です。
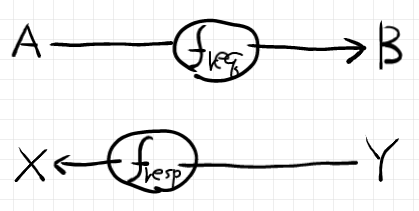
以下の過去記事に、射の捻じれ対が実際に使われている例があります。
以下の絵は、「圏論的レンズ 最初の一歩: ストリング図を中心に」で出した“退化したレンズ”の絵ですが、これも射の捻じれ対になっています。
反対圏を表す $`\hyp^\op`$ を関手にも使うことにします(この記事内では使ってませんが)。「層化ストリング図 // 裏返し反変関手」で導入した記法を使います。それは:
- $`\mrm{Rev}_\cat{C} : \cat{C} \to \cat{C}^\op`$ (ホントの反変関手)
- $`{\mrm{Rev}_\cat{C}}^{-1} = \mrm{Rev}_{\cat{C}^\op} : \cat{C}^\op \to \cat{C}`$ (ホントの反変関手)
$`F:\cat{C} \to \cat{D}`$ に対して、$`F^\op`$ を次のように定義します。アスタリスクは、関手の図式順結合記号です。
$`\quad
F^\op := {^\mrm{rev}F^{\mrm{rev}}} = \mrm{Rev}_{\cat{D}^\op} * F * \mrm{Rev}_\cat{D}
: \cat{C}^\op \to \cat{D}^\op
`$
例えば、プロ関手 $`P : \cat{C}^\op\times \cat{D} \to {\bf Set}`$ に対して $`\hyp ^\op`$ を作用させると:
$`\quad P^\op : \cat{C}\times \cat{D}^\op \to {\bf Set}^\op`$
余域の圏が集合圏の反対圏になるので、もはや通常のプロ関手ではありません。プロ関手の転置(引数の順番の入れ替え)$`P^\mrm{t}`$ とは別物です。
$`\quad P^\mrm{t} : \cat{D}\times \cat{C}^\op \to {\bf Set}`$
反対圏や反変関手はややこしいので注意しましょう(「反対圏と反変関手はややこしい」参照)。
状態遷移系
よくある状態遷移系の定義は、アルファベット(ラベルの集合)$`\Sigma`$(なぜか習慣として大文字シグマを使う)と状態の集合〈状態空間〉 $`S`$ *2があり、次のような遷移写像〈反応写像〉が備わっている構造です。
$`\quad \delta : \Sigma \times S \to S \In {\bf Set}`$
アルファベット $`\Sigma`$ から自由モノイド〈クリーネスター〉 $`\Sigma^*`$ を作って、遷移写像を次の形に拡張するのも普通です。
$`\quad \lambda : \Sigma^* \times S \to S \In {\bf Set}`$
ここで出てきた $`\lambda`$ は「ラムダ記法のラムダ」でもなければ「左単位律同型のラムダ」でもありません。左からのモノイド作用を表すラムダです。
アルファベットからの自由モノイドに限らず、任意のモノイドの左作用を考えるなら:
$`\quad \lambda : \u{M} \times S \to S \In {\bf Set}`$
ここで、$`M = (\u{M}, m, e)`$ はモノイドで、$`\u{M}`$ はモノイドの台集合です。
上記の形 $`(M, S, \lambda)`$ として状態遷移系を定義したときは、満たすべき法則〈公理〉は次のようになります。
- $`\forall a, b\in \u{M}.\forall s\in S.\, \lambda(a, \lambda(b, s)) = \lambda(m(a,b), s)`$
- $`\forall s\in S.\, \lambda(e, s) = e`$
$`\lambda`$ の中置演算子記号として '$`\lact`$' 、$`m`$ の中置演算子記号として '$`\cdot`$' を使うと、法則は次のように書けます。
- $`\forall a, b\in \u{M}.\forall s\in S.\, a \lact (b \lact s) = (a \cdot b)\lact s`$
- $`\forall s\in S.\, e\lact s = s`$
この法則を満たす構造 $`(M, S, \lambda)`$ を左状態遷移系〈left state transition system〉と呼びます。左刺激反応系〈左刺激応答系 | left stimuli-response system〉も左状態遷移系の同義語として使います。
- モノイド $`M`$ を、左状態遷移系の左刺激モノイド〈left stimuli monoid〉と呼ぶことにします。
- 集合 $`S`$ を、左状態遷移系の状態空間〈state space〉と呼びます。
- 写像 $`\lambda`$ を、左状態遷移系の左作用〈left action〉と呼びます。
左状態遷移系を $`A`$ で表したとき、次のように書きます。
$`\quad A = (\mrm{LStim}(A), A_\mrm{ss}, A_\mrm{lact})`$
書き方が統一性に欠けますが、こういうのは習慣やなりゆきがあるので目くじら立てないでください(「構造とその素材の書き表し方」参照)。
$`A, B`$ が2つの左状態遷移系のとき、これらのあいだの準同型写像 $`\varphi`$ は、左刺激モノイドのあいだのモノイド射と、状態空間のあいだの写像の組 $`\varphi = (\varphi_\mrm{LStim}, \varphi_\mrm{ss})`$ で次の図式を可換にするものです。
$`\require{AMScd}
\quad \begin{CD}
\u{\mrm{LStim}(A)}\times A_\mrm{ss} @>{A_\mrm{lact}}>> A_\mrm{ss}\\
@V{\varphi_\mrm{LStim} \times \varphi_\mrm{ss}}VV @VV{\varphi_\mrm{ss}}V\\
\u{\mrm{LStim}(B)}\times B_\mrm{ss} @>{B_\mrm{lact}}>> B_\mrm{ss}
\end{CD}\\
\quad\text{commutative in } {\bf Set}
`$
左状態遷移系を対象として、左状態遷移系の準同型写像を射とする左状態遷移系の圏〈category of left state transition systems〉が構成できます。これを $`{\bf LSTS}`$ と書きます。
モノイド $`M \in |{\bf Mon}|`$ を固定して、$`\mrm{LStim}(A) = M`$ であるような左状態遷移系だけを考えて、射は $`\varphi_\mrm{LStim} = \id_M`$ である準同型写像に限ると、これも圏になります。この圏は $`{\bf LSTS}(M)`$ と書きます。
モノイドの左作用の代わりに右作用を考えると右状態遷移系〈right state transition system〉を定義できます。右状態遷移系 $`B`$ は次のように書きます。
$`\quad B = (\mrm{RStim}(B), B_\mrm{ss}, B_\mrm{ract})`$
右状態遷移系の法則は、中置演算子記号 '$`\ract`$' を使って次のように書けます。$`N := \mrm{RStim}(B)`$ 、$`S := B_\mrm{ss}`$ としています。
- $`\forall a, b\in \u{N}.\forall s\in S.\, (s \ract a) \ract b = s \ract (a \cdot b)`$
- $`\forall s\in S.\, s \ract e = s`$
左状態遷移系と同様にして右状態遷移系の圏〈category of right transition systems〉 $`{\bf RSTS}`$ を構成できます。モノイド $`N`$ に対する $`{\bf RTST}(N)`$ も同様です。
双状態遷移系
両側状態遷移系〈two-sided state transition system〉または双状態遷移系〈{state}? bitransition system〉は、2つのモノイドがそれぞれ左から/右から作用する状態遷移系です。
双状態遷移系を $`C`$ で表したとき、次のように書きます。
$`\quad C = (\mrm{LStim}(C), \mrm{RStim}(C), C_\mrm{ss}, C_\mrm{bact})`$
ここで、$`C_\mrm{bact}`$ は双状態遷移系の双作用〈biaction〉と呼びます。
記法を簡略化するため、次のように置きましょう。
$`\quad M := \mrm{LStim}(C) \; \in |{\bf Mon}|\\
\quad N := \mrm{RStim}(C)\; \in |{\bf Mon}|\\
\quad S := C_\mrm{ss} \; \in |{\bf Set}|\\
\quad \beta := C_\mrm{bact} \;: \u{M}\times S\times \u{N} \to S \In {\bf Set}
`$
双状態遷移系が満たすべき法則〈公理〉は次のようになります。モノイド演算とモノイド単位は左右ともに $`\cdot`$ と $`e`$ を使っています。
- $`\forall a, a'\in \u{M}.\forall b, b'\in \u{N}.\forall s\in S.\, \beta(a, \beta(a', s, b'), b) = \beta( a \cdot a', s, b' \cdot b )`$
- $`\forall s\in S.\, \beta(e, s, e) = s`$
次の略記も使います。
$`\quad a \lact s \ract b := \beta(a, s, b)\\
\quad a \lact s := a \lact s \ract e \ := \beta(a, s, e)\\
\quad s \ract b := e \lact s \ract b \ := \beta(e, s, b)
`$
この略記で法則を書くと:
- $`\forall a, a'\in \u{M}.\forall b, b'\in \u{N}.\forall s\in S.\, a\lact (a' \lact s \ract b')\ract b = (a \cdot a')\lact s \ract (b' \cdot b)`$
- $`\forall s\in S.\, e\lact s \ract e = s`$
特定の $`b\in N`$ に対して、$`\lambda(\hyp, \hyp) := \beta(\hyp, \hyp, b)`$ と置くと、以下の左状態遷移系ができます。
$`\quad (M, S, \lambda) \; \in |{\bf LSTS}|`$
特定の $`a\in M`$ に対して、$`\rho(\hyp, \hyp) := \beta(a, \hyp, \hyp)`$ と置くと、以下の右状態遷移系ができます。
$`\quad (N, S, \rho) \; \in |{\bf RSTS}|`$
$`C, D`$ が2つの双状態遷移系のとき、これらのあいだの準同型写像 $`\psi`$ は、左刺激モノイドのあいだのモノイド射と、右刺激モノイドのあいだのモノイド射と、状態空間のあいだの写像の組 $`\psi = (\psi_\mrm{LStim}, \psi_\mrm{RStim}, \psi_\mrm{ss})`$ で次の図式を可換にするものです。
$`\require{AMScd}
\quad \begin{CD}
\u{\mrm{LStim}(C)}\times C_\mrm{ss}\times\u{\mrm{RStim}(C)} @>{C_\mrm{bact}}>> C_\mrm{ss}\\
@V{\psi_\mrm{LStim} \times \psi_\mrm{ss}\times \psi_{\mrm{RStim}}}VV @VV{\psi_\mrm{ss}}V\\
\u{\mrm{LStim}(D)}\times D_\mrm{ss}\times\u{\mrm{RStim}(D)} @>{D_\mrm{bact}}>> D_\mrm{ss}
\end{CD}\\
\quad\text{commutative in } {\bf Set}
`$
双状態遷移系を対象として、双状態遷移系の準同型写像を射とする双状態遷移系の圏〈category of {state}? bitransition systems〉が構成できます。これを $`{\bf BiSTS}`$ と書きます。
2つのモノイド $`M, N \in |{\bf Mon}|`$ を固定して、$`\mrm{LStim}(C) = M, \mrm{RStim}(C) = N`$ であるような左状態遷移系だけを考えて、射は $`\psi_\mrm{LStim} = \id_M, \psi_\mrm{RStim} = \id_N`$ である準同型写像に限ると、これも圏になります。この圏は $`{\bf BiSTS}(M, N)`$ と書きます。
関手としての状態遷移系
モノイド $`M`$ を、単一対象の圏と考えます。唯一つの対象は $`\star`$ とします。
$`\quad |M| = \mrm{Obj}(M) = \{\star\}\\
\quad \mrm{Mor}(M) = \u{M}\\
\quad M(\star, \star) = \u{M}\\
\quad \id_\star = e
`$
モノイド演算の記号 '$`\cdot`$' は射の結合の図式順演算子記号 '$`;`$' と同じとみなします。反図式順が多数派*3なので注意してください。
$`A`$ を、単一対象の圏と考えたモノイド $`M`$ から集合圏への反変関手(つまり前層)とします。
$`\quad A: M^\op \to {\bf Set} \In {\bf CAT}\\
\text{i.e. }A \in [M^\op, {\bf Set}]
`$
以下、関手の対象パートへの引数渡しにはブラケットを使い、射パートへの引数渡しには丸括弧を使うことにします。
$`\quad S := A_\mrm{obj}[\star] \;\in |{\bf Set}|\\
\For a \in M(\star, \star)\\
\quad A_\mrm{mor}(a) : S \to S \In {\bf Set}\\
\text{i.e. } A_\mrm{mor}(a) \in \mrm{Map}(S, S)
`$
この状況で、写像 $`\lambda`$ を次のように定義します。
$`\lambda : M(\star, \star) \times S \to S \In {\bf Set}\\
\For a \in M(\star, \star), s \in S\\
\quad \lambda(a, s) := A_\mrm{mor}(a)(s) \; \in S
`$
写像 $`\lambda`$ が左状態遷移系の左作用になることはすぐ分かります。計算例は:
$`\For a, b \in M(\star, \star), s \in S\\
\quad \lambda(a, \lambda(b, s)) \\
\quad = A_\mrm{mor}(a)(A_\mrm{mor}(b)(s))\\
\quad = (A_\mrm{mor}(a)\circ A_\mrm{mor}(b)) (s)\\
\quad = A_\mrm{mor}(a ; b) (s)\\
\quad = A_\mrm{mor}( a\cdot b) (s)\\
\quad = \lambda( a\cdot b, s)
`$
ここで、'$`\circ`$' は関数結合の反図式順記号で、'$`;`$' は圏の射の結合の図式順記号です。$`A`$ が反変関手なので、上のような計算ができます。
結局、前層(反変関手)$`A`$ は次の左状態遷移系を定義します。
$`\quad ( (M(\star, \star), ;, \id_\star), A_\mrm{obj}[\star], \lambda)`$
逆に、左状態遷移系が与えられると、それから前層を作れるので、“$`M`$ を左刺激モノイドとする左状態遷移系”と“$`M`$ 上の前層”を同一視します。そして、左状態遷移系と前層の折衷案的な記法で書くことにします。
$`\quad A = (M^\op, A_\mrm{ss}, A_\mrm{lact})`$
$`M`$ が関手の域である圏、$`\hyp^\op`$ で反変関手であることを示しています。$`A_\mrm{ss}`$ は関手の対象パート(状態空間相当)、$`A_\mrm{lact}`$ が関手の射パート(左作用相当)です。さらに次の略記を使用します。
$`\For a, b \in \u{M} = M(\star, \star)\\
\For s \in S = A_\mrm{ss}[\star]\\
\quad a\cdot b := a;b \\
\quad a\lact_{A} s = a\lact s := A_\mrm{lact}(a)(s)
`$
余前層(共変関手)と右状態遷移系も同様に同一視可能で、右状態遷移系と余前層の折衷案的な記法で書くことにします。
$`\quad B = (N, B_\mrm{ss}, B_\mrm{ract})`$
次の略記を使用します。
$`\For c, d \in \u{N} = N(\star, \star)\\
\For s \in S = B_\mrm{ss}[\star]\\
\quad c\cdot d := c;d \\
\quad s\ract_{B} c = s \ract c := B_\mrm{ract}(c)(s)
`$
プロ関手 $`C: M^\op \times N \to {\bf Set}`$ は双状態遷移系と同一視可能です。右状態遷移系とプロ関手の折衷案的な記法で書くことにします。
$`\quad C = (M^\op, N, C_\mrm{ss}, C_\mrm{bact})`$
次の略記を使用します。
$`\For a \in \u{M} = M(\star, \star)\\
\For c \in \u{N} = N(\star, \star)\\
\For s \in S = C_\mrm{ss}[\star]\\
\quad a \lact_C s \ract_{C} c = a \lact s \ract c := C_\mrm{bact}(a, c)(s)
`$
双状態遷移系としてのプロ関手
ここから先は、プロ関手〈profunctor〉を双状態遷移系とみなす話をします。プロ関手については、次の過去記事で述べています。
プロ関手の実体は次の形をした双関手〈二項関手〉です。
$`\quad P:\cat{C}^\op \times \cat{D} \to {\bf Set}\In {\bf CAT}`$
おおざっぱに言えば、「関手 : プロ関手 = 関数 : 関係」という“比例式”が成立します。上記双関手のプロ関手としての向きをどう決めるかは、人により違います。
$`\quad P : \cat{C} \to \cat{D} \In {\bf Prof}\\
\text{or}\\
\quad P : \cat{D} \to \cat{C} \In {\bf Prof}
`$
関手と違って、プロ関手は方向の逆転が容易なので、別にどっちでもかまいません。この記事では、プロ関手としての方向は特に使いません。
前層、余前層、プロ関手を状態遷移系と解釈できます。つまり、状態空間に左から、または右から、あるいは両側から刺激〈stimulus〉が作用する構造ですね。刺激達〈simuli〉はモノイドに限らず一般の圏を許します。状態空間は、単一の集合ではなくてインデックス付き集合〈indexed set〉になります。
インデックス付き集合のインデキシング集合〈indexing set〉は圏の対象集合ですが、インデックスらしい気分を出すために $`I := |\cat{C}|`$ と置きます。状態空間となるインデックス付き集合(ファミリーと言っても同じ)は次のようです。
$`\quad I \ni i \mapsto F_\mrm{ss}[i] \in |{\bf Set}|`$
$`F`$ が前層=左状態遷移系の場合ならば、左作用(の雰囲気)は次の図のようになります。
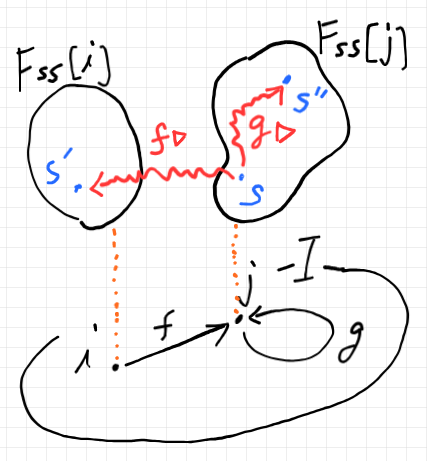
インデキシング集合 $`I = |\cat{C}|`$ の各点 $`i`$ に対して、個別の状態空間 $`F_\mrm{ss}[i]`$ が“ファイバーとして生えて”います。左刺激による状態遷移は、同じファイバーのなかに限らず、異なるファイバー間での遷移もありえます。
2つの異なるインデックス点 $`i, j`$ のあいだに射 $`f:i \to j \In \cat{C}`$ があると、$`f`$ から(反変的に)誘導された左作用 $`f\lact`$ は、ファイバー $`F_\mrm{ss}[j]`$ からファイバー $`F_\mrm{ss}[i]`$ への遷移を引き起こします。
$`\quad F_\mrm{ss}[j] \ni s \overset{f\lact}{\leadsto} s' \in F_\mrm{ss}[i]`$
ひとつのインデックス点 $`j`$ でループする自己射 $`g:j \to j \In \cat{C}`$ に対しては、左作用 $`g\lact`$ は、ひとつのファイバー $`F_\mrm{ss}[j]`$ 内の遷移を引き起こします。
$`\quad F_\mrm{ss}[j] \ni s \overset{g\lact}{\leadsto} s'' \in F_\mrm{ss}[j]`$
状態遷移をイメージした上の絵は、前層 $`F:\cat{C}^\op \to {\bf Set}`$ に対する要素の圏〈category of elements〉を描画したものです。上の絵で赤く描いた状態遷移の矢印は、要素の圏の射です。要素の圏はグロタンディーク構成によるファイバー付き圏〈{fibred | fibered} category〉の特別なもので、ファイバーが離散圏(事実上、単なる集合)であるものです。
グロタンディーク構成については、次の過去記事に説明があります。
プロ関手 $`P`$ の場合は、状態空間であるインデックス付き集合のインデキシング集合は次の形になります。
$`\quad |\cat{C}^\op\times \cat{D}| = |\cat{C}^\op| \times |\cat{D}|`$
もう、気分を出す必要はないでしょうから、$`|\cat{C}^\op| \times |\cat{D}|`$ のまま使います。インデックスは $`(\o{a}, d)`$ のようなペアになり、対応する状態空間のファイバーは $`P_\mrm{ss}[\o{a}, d]`$ です。反対圏の対象に上線を引いているのは念のためで、$`a`$ と $`\o{a}`$ は同一対象です。
2つのインデックスペアのあいだを結ぶ射は、最初の節で述べた捻じれ対になります。捻じれ対 $`(\o{f}, g)`$ から誘導された双作用〈両側作用〉は、捻じれ対の順方向($`g`$ の方向)に沿った状態遷移を引き起こします。次の絵のような“感じ”です。
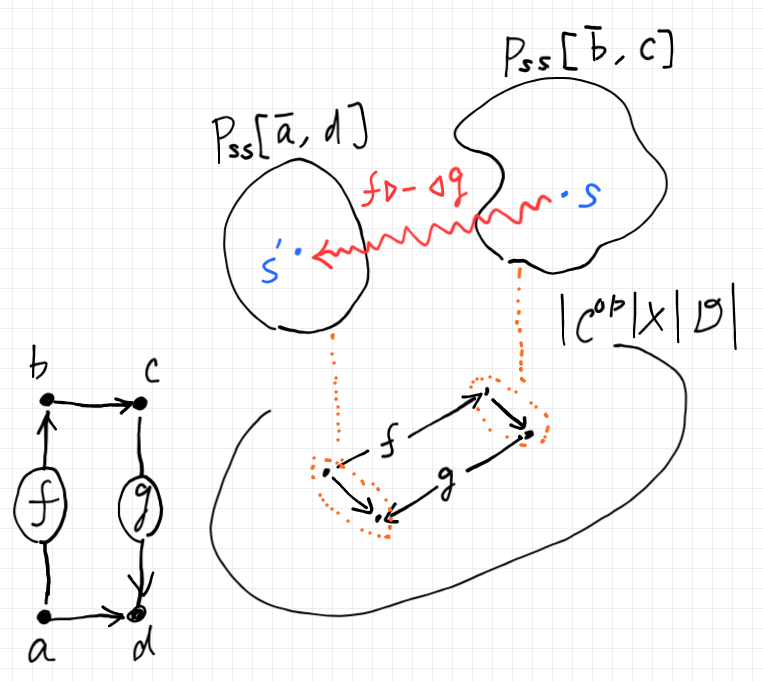
左から作用する $`f`$ は $`\cat{C}^\op`$ の射なので、$`\o{f}`$ と書いたほうが紛れはないですが、混乱の心配がなければ上線は省略してもいいでしょう。逆に、混乱してしまうときは上線を利用するといいです。
特定の状態点 $`s`$ からの状態遷移(絵のなかの赤いグニグニ矢印)は次のように書けます。
$`\quad P_\mrm{ss}[\o{b}, c] \ni s \overset{f\lact\hyp \ract g}{\leadsto} s' \in P_\mrm{ss}[\o{a}, d]`$
左状態遷移系と右状態遷移系のテンソル積
$`F:\cat{C}^\op \to {\bf Set}`$ が前層、$`G: \cat{C} \to {\bf Set}`$ が余前層とします。言い方を変えると、$`F`$ は左状態遷移系で $`G`$ は右状態遷移系です。$`F, G`$ は同じ刺激圏 $`\cat{C}`$ を共有します。
$`\quad F = (\cat{C}^\op, F_\mrm{ss}, F_\mrm{lact})\\
\quad G = (\cat{C}, G_\mrm{ss}, G_\mrm{ract})
`$
この状況で、$`F`$ と $`G`$ から新しい双状態遷移系を作ります。できた双状態遷移系を、$`F`$ と $`G`$ のテンソル積〈tensor product〉と呼び、次のように書きます。
$`\quad F \otimes G = F\otimes_\cat{C} G : \cat{C}^\op \times \cat{C} \to {\bf Set}`$
「テンソル積」という言葉は使われ過ぎで、もはやマジックワード*4になっています。が、代わりの言葉も見つからないので、テンソル積と呼んでおきます。別な文脈での「テンソル積」は別な“テンソル積”となるでしょう。
$`H := F \otimes G`$ と置いて、双状態遷移系(あるいはプロ関手)$`H`$ を定義しましょう。まず、$`H`$ の状態空間であるインデックス付き集合は次のように定義します。
$`\For \o{a} \in |\cat{C}^\op|, b\in |\cat{C}| \\
\quad H_\mrm{ss}[\o{a}, b] := F_\mrm{ss}[\o{a}] \times G_\mrm{ss}[b] \; \in |{\bf Set}|
`$
次に、状態空間に対する双作用を定義しますが、次の刺激を考えます。
$`\quad (\o{f}, g)
\:\text{ where } f:a \to b, g: c \to d \In \cat{C}
`$
捻じれ対の絵で描くと次のようです。
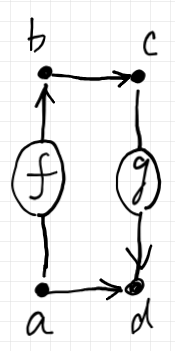
この刺激に対する双作用〈両側作用〉を次のように定義します。
$`\For (s, t) \in H_\mrm{ss}[\o{b}, c]\\
\quad \o{f}\lact (s, t) \ract g := (\o{f}\lact s, t\ract g)
`$
もう少し丁寧に書くと:
$`\For s \in F_\mrm{ss}[\o{b}], t \in G_\mrm{ss}[c]\\
\quad \o{f}\lact_H (s, t) \ract_H g := (\o{f}\lact_F s, t\ract_G g)
`$
これが実際に双作用になっているのを確認するには、次のような刺激と遷移を考えます。
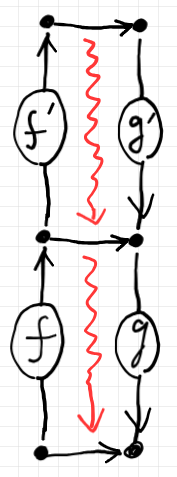
$`(s, t)`$ に対する双作用を計算すると:
$`\quad \o{f} \lact (\o{f'} \lact (s, t) \ract g') \ract g\\
= \o{f} \lact (\o{f'} \lact s, t \ract g') \ract g\\
= (\o{f} \lact (\o{f'} \lact s), (t \ract g') \ract g )\\
= ( (\o{f ; f'}) \lact s, t \ract( g' ; g) )
`$
恒等射ペアによる双作用で何も起きないことも明らかでしょう。
以上で、左状態遷移系 $`F`$ と右状態遷移系 $`G`$ のテンソル積双状態遷移系 $`H := F \otimes G`$ が定義されました。
幾つかの拡張の方向
この記事では、前層 $`F`$、余前層 $`G`$、プロ関手 $`P`$ を状態遷移系として解釈しました。
$`\quad F: \cat{C}^\op \to {\bf Set} \In {\bf CAT}\\
\quad G: \cat{C} \to {\bf Set} \In {\bf CAT}\\
\quad P: \cat{C}^\op\times \cat{D} \to {\bf Set} \In {\bf CAT}
`$
関与する圏をもっと増やして、例えば $`\cat{C}^\op\times \cat{D}\times \cat{E}^\op \to {\bf Set}`$ のような、反変・共変が混じった多項関手ならどうだろう? と思い至ります。この方向で考えてみたのが、米田テンソル計算です。以下の過去記事が第一回兼ハブ記事になっています。
前層・余前層・プロ関手では、関手の余域は集合圏 $`{\bf Set}`$ に固定しています。この場合の集合圏は、行列・テンソル計算におけるスカラー環のような役割を持っています。スカラーを変更すれば、計算体系は変わってきます。集合圏の代わりに次のような圏を“スカラーの圏”に採用する案があります。
- アーベル群〈可換群〉と群の準同型写像の圏 $`{\bf Ab}`$
- ベクトル空間と線形写像の圏 $`{\bf Vect}_K`$ ($`K`$ は適当な体)
- 可換モノイドとモノイド準同型写像の圏 $`{\bf CMon}`$
- 順序集合と単調写像の圏 $`{\bf Ord}`$
- 一般的・抽象的なベナブー・コスモス〈Bénabou cosmos〉(完備かつ余完備な対称モノイド閉圏)
多項関手(単項関手含む)としての前層・余前層・プロ関手の域は、特に条件も追加構造もないプレーンな圏でした。条件や追加構造を付けた圏を域にすることも考えられます。
- 一般の圏ではなくて、亜群(の直積)を域とする。
- モノイド圏(の直積)や対称モノイド圏(の直積)を域とする。多項関手はモノイド関手を考える。
- 特定の種類の極限または余極限を持つ圏を域とする。多項関手は連続または余連続な関手を考える。
拡張したケースにおいて、状態遷移系としての解釈がどこまで可能かは興味深い課題です。
*1:[追記]最初に見た論文は憶えてないのですが、 "(Co)ends for representations of tensor categories" by Noelia Bortolussi, Martín Mombelli では上線記法が使われています。Preliminaries and Notation. に、 $`F^\op(\o{M} ) = \o{F(M)}, F^\op(\o{f}) = \o{F(f)}`$ という関係式も書いてあります。[/追記]
*2:状態空間も、なぜか習慣として大文字 Q が多いのですが、ここでは S を使いました。
*3:例えば、行列の掛け算 $`A B`$ は $`A B = A\circ B`$ であって、$`A B = A; B`$ ではありません。
*4:「マジックワードとは、すごく意味がありそうなのによく考えるとわからなくなる、いわば思考停止を招く言葉」だそうです。