アドホック随伴系と自由対象・台対象 - 檜山正幸のキマイラ飼育記 (はてなBlog)

割とよく使われる概念であっても、合意された名前がないと、ソレについて語ることが困難です。随伴系〈adjunction | adjoint system〉にはなっていない“随伴系もどき”はけっこう登場するのですが、これといった名前はないようです。ここでは、ソレをアドホック随伴系と呼んで語ることにします。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\twoto}{\Rightarrow }
\newcommand{\In}{\text{ in } }
%\newcommand{\Iff}{\Leftrightarrow }
\newcommand{\hyp}{\text{－} }
\newcommand{\op}{\mathrm{op} }
\newcommand{\id}{\mathrm{id} }
%
\newcommand{\For}{\text{For } }
`$

内容：

代数的な随伴系：名付けの憂鬱
自然なホムセット同型による随伴系
アドホック随伴系
アドホック随伴系のアドホック単位
アドホック単位と転置
そしてそれから

関連する記事：

圏論の普遍性が難しい理由

代数的な随伴系：名付けの憂鬱

高次元の代数系として定義される随伴系とは何であるか？過去記事「代数的な随伴系から自然なホムセット同型へ」の一部をそのまま引用します。

代数的な随伴系（単位と余単位を含む代数系）は、圏の2-圏のなかに実現される等式的な構造で、次の構成素〈constituent〉を持ちます。$`\mrm{Id}_{\hyp}`$ は恒等関手、$`\mrm{ID}_{\hyp}`$ は恒等自然変換です。

0次元構成素： 2つの圏 $`\cat{C}, \cat{D}`$

1次元構成素： 2つの関手 $`F:\cat{C}\to \cat{D}, G:\cat{D}\to \cat{C}`$

2次元構成素： 2つの自然変換 $`\eta:: \mrm{Id}_{\cat{C}} \twoto F*G, \varepsilon :: G*F \twoto \mrm{Id}_{\cat{D}}`$ （$`\eta`$ が単位で、$`\varepsilon`$ が余単位）

3次元構成素： 2つの等式 $`\Gamma ::: (\eta * F);(F * \varepsilon) = \mrm{ID}_F, \Delta ::: (G*\eta); (\varepsilon * G) = \mrm{ID}_G`$ （ニョロニョロ関係式〈snake {relation | equation | identity} 〉）

これで、代数的な随伴系は定義されます。このテの定義を書くとき毎回思うことが、「名前（割り当てる記号と用語）が邪魔だなー」「名前を決めるのが嫌だな、決めたくないなー」。

なぜかと言うと、抽象的構造は確定的でも、名前は恣意的に変動してしまうからです。実際、以下は別なタイミングで記述した代数的な随伴系の定義です -- 色付きLaTeX（MathJax）で書いたものを画面キャプチャ〈スクショ〉した画像ですが。

同じ人間〈檜山〉が書いているので、似かよってはいますが、微妙に違っています。抽象的構造を記述する際に、その構成素〈constituent〉達の名前（記号ラベルと役割り名）をどう付けるかはどうでもいいのですが、「どうでもいい」ことが周知されてもいないのです。それに、名前のズレがあると「どうでもいい」と思っている僕も、実は嫌な気分になります。名前を置き換える作業がけっこうな手間とストレスになるからです。あー、名付けは憂鬱だ！

名付けを回避するために、ラベルなしのペースティング図で構造を記述したものが以下です。赤または青のセル（点や矢印）が構造の構成素で、黒のセルは恒等セル（恒等k-射に対応する図形）です。色は、上のテキスト記述とあわせています。

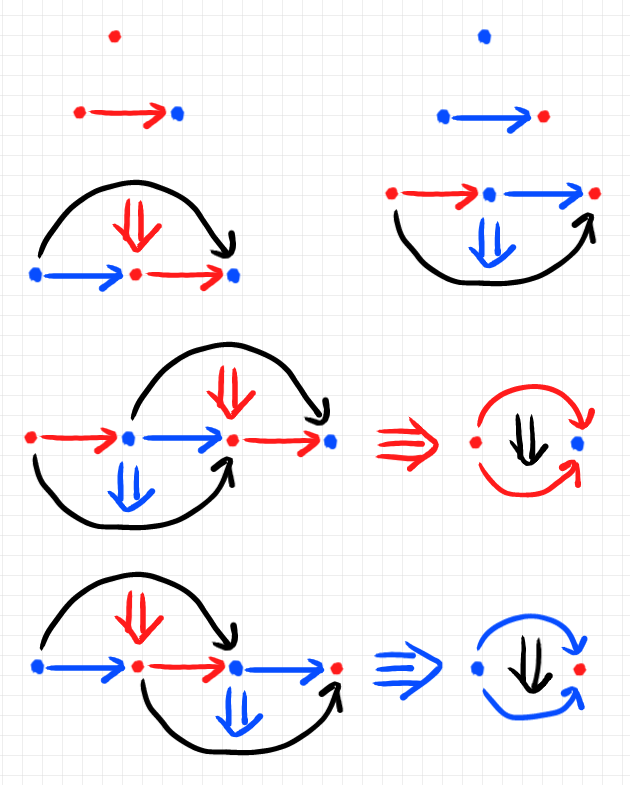
同様なことをストリング図（描画方向：上から下、左から右）で表すと以下。バッテンは文字エックスではなくてエリアを意味する印です、ちょっと紛らわしかった。恒等射は黒点線ワイヤーまたは黒点線輪郭のノードです。3-射はストリング図の描き換え〈変形〉で表しています。

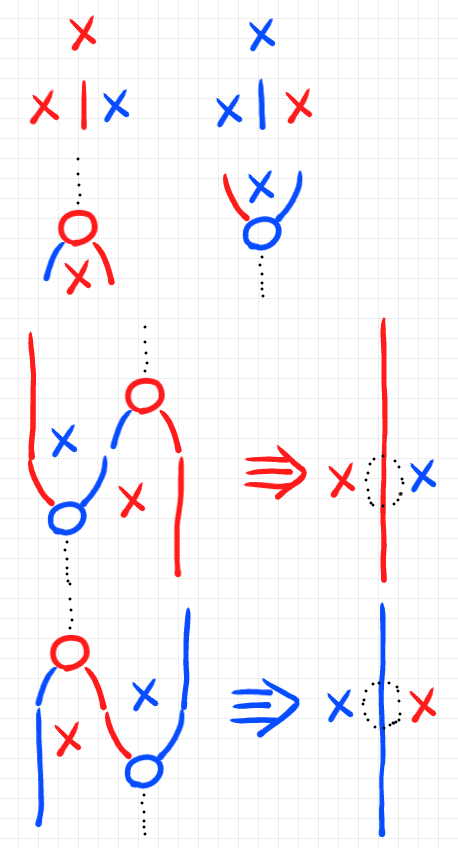
絵図ならば名付けの憂鬱から開放されます。なぜなら、絵図のなかの構成素は「これ」とゆび差して直示〈ちょくじ〉できるからです。‥‥ ということは、ゆび差し可能な対話環境でないと使えない。そうです、対面〈face to face〉、動画、アニメーションなどでないと直示は無理です。ハァ（ため息）。

致し方ないので、この記事でローカルに使う名前（記号ラベルと役割り名）を次のように決めます。

記号ラベル	役割り名
$`L`$	左随伴関手＝随伴系の左関手
$`R`$	右随伴関手＝随伴系の右関手
$`\eta`$	随伴系の単位
$`\varepsilon`$	随伴系の余単位

構成素のプロファイル（域・余域の仕様）は以下のとおり。

$`\quad L :\cat{C} \to \cat{D} \In {\bf CAT}\\
\quad R :\cat{D} \to \cat{C} \In {\bf CAT}\\
\quad \eta :: \mrm{Id}_\cat{C} \twoto L*R \In {\bf CAT}\\
\quad \varepsilon :: R*L \twoto \mrm{Id}_\cat{C} \In {\bf CAT}
`$

2つのニョロニョロ法則（等式＝ 3-射）は、明示的に参照しないで暗黙に仮定します（よって、名前は不要）。

自然なホムセット同型による随伴系

随伴系の別な定義として、自然なホムセット同型を使う定義があります。以下の構成素は代数的な定義と同じです。

$`\quad \cat{C},\cat{D}, L, R`$

以下は新しい構成素です。

記号ラベル	役割り名
$`\tau`$	随伴系の転置
$`\upsilon`$	随伴系の反転置

新しい構成素のプロファイルは以下のとおり。

$`\quad \tau :: \cat{D}(L(\hyp), \hyp) \twoto \cat{C}(\hyp, R(\hyp)) : \cat{C}^\op\times \cat{D} \to {\bf Set} \In {\bf CAT}\\
\quad \upsilon :: \cat{C}(\hyp, R(\hyp)) \twoto \cat{D}(L(\hyp), \hyp) : \cat{C}^\op\times \cat{D} \to {\bf Set} \In {\bf CAT}
`$

新しい法則（等式＝ 3-射）は次です。

$`\quad \mrm{transp} ::: \tau ; \upsilon = \mrm{ID}_{\cat{D}(L(\hyp), \hyp)} \\
\qquad :: \cat{D}(L(\hyp), \hyp) \twoto \cat{D}(L(\hyp), \hyp) : \cat{C}^\op\times \cat{D} \to {\bf Set} \In {\bf CAT}\\
\quad \mrm{untransp} ::: \upsilon ; \tau = \mrm{ID}_{\cat{C}(\hyp, R(\hyp))} \\
\qquad :: \cat{C}(\hyp, R(\hyp)) \twoto \cat{C}(\hyp, R(\hyp)) : \cat{C}^\op\times \cat{D} \to {\bf Set} \In {\bf CAT}
`$

この2つの法則は、次の一言で置き換え可能です。

自然変換 $`\tau`$ は可逆である。

よって、構成素のラベル $`\upsilon, \mrm{transp}, \mrm{untransp}`$ は不要で、次のような簡略な書き方で事情を示すことができます。

$`\quad \cat{D}(L(\hyp), \hyp) \overset{\tau}{\cong} \cat{C}(\hyp, R(\hyp))`$

可逆な自然変換に付けられたラベル $`\tau`$ も暗黙化されて、表面には現れないこともあります。

代数的に定義された随伴系から自然なホムセット同型を得る方法は次の過去記事に書いています。

代数的な随伴系から自然なホムセット同型へ

逆に、自然なホムセット同型から代数的な定義（の一部）を得る方法は次の過去記事に書いています。

随伴の自然なホムセット同型から単位自然変換へ

アドホック随伴系

前節までは、通常の随伴系の話でした。ここから先は、出来そこないの随伴系の話をします。

まず、強引で理不尽な用語法を導入します。強引で理不尽な用語法は、僕個人やこの記事ローカルなものではなくて、世間で使われているものです*1。

随伴系の典型例といえば自由忘却随伴系〈free-forgetful adjunction〉なので、

随伴系の左関手の同義語として「自由関手〈free functor〉」を使う。
随伴系の右関手の同義語として「忘却関手〈forgetful functor〉」を使う。
「自由関手＝左関手」の値 $`L(A)`$ を「自由対象〈free object〉」と呼ぶ。
「忘却関手＝右関手」の値 $`R(Y)`$ を「台対象〈underlying object〉」と呼ぶ。

アドホック随伴系〈ad-hoc {adjunction | adjoint system}〉（これは個人的ローカルな用語）はニ種類あります。

自由関手（＝左関手）が存在するが、忘却関手（＝右関手）は欠如しているケース
忘却関手（＝右関手）が存在するが、自由関手（＝左関手）は欠如しているケース

どちらか一方を説明すれば、「残りも同様」なので、忘却関手（＝右関手）が存在していて自由関手が欠如しているケースのアドホック随伴系を説明します。

欠如がない通常の随伴系では、次のようなホムセット同型があります。

$`\quad \cat{D}(L(A), Y) \cong \cat{C}(A, R(Y))`$

もし、左関手（＝自由関手）が欠如していて、単に $`L(A)`$ に相当する対象 $`W`$ が在るだけなら次のようになります。

$`\quad \cat{D}(W, Y) \cong \cat{C}(A, R(Y))`$

忘却関手（＝右関手）の記号ラベルは（気持ちの問題から）$`U`$ に変更します。

$`\quad \cat{D}(W, Y) \cong \cat{C}(A, U(Y))`$

自由関手は存在してませんが、対象 $`W\in |\cat{D}|`$ は、対象 $`A\in |\cat{C}|`$ の自由対象〈free object〉だと言ってもいいでしょう（強引で理不尽だけどね）。

ホムセット同型に出現する $`Y`$ は何でもよいので、無名ラムダ変数（ハイフン）に置き換えると：

$`\quad \cat{D}(W, \hyp) \cong \cat{C}(A, U(\hyp))`$

この状況が、自由関手が欠如したアドホック随伴系を定義します。

きちんと構成素を列挙すれば：

0次元構成素： 2つの圏 $`\cat{C}, \cat{D}`$
1次元構成素：関手 $`U:\cat{D}\to \cat{C}`$ （忘却関手）
1次元構成素：対象 $`W \in |\cat{D}|`$ （自由対象）
1次元構成素：対象 $`A \in |\cat{C}|`$ （台対象）
2次元構成素： 2つの自然変換 $`\varphi :: \cat{D}(W, \hyp) \twoto \cat{C}(A, U(\hyp)),\; \psi :: \cat{C}(A, U(\hyp)) \twoto \cat{D}(W, \hyp)`$
3次元構成素： 2つの等式、一言でいえば「$`\varphi`$ と $`\psi`$ は互いに逆」

圏の対象が1次元構成素なのは、対象は次のような自明圏〈単位圏〉$`{\bf I}`$ *2からのポインティング関手と同一視可能だからです。

$`\quad W^\sim : {\bf I} \to \cat{D} \In {\bf CAT}\\
\quad A^\sim : {\bf I} \to \cat{C} \In {\bf CAT}
`$

互いに逆な自然変換の片方 $`\varphi`$ だけに注目して、これをアドホック随伴系の転置〈transposition〉と呼ぶことにします。$`\psi = \varphi^{-1}`$ は反転置〈opposite-transposition | untransposition〉です。随伴系の場合の $`\tau, \upsilon`$ に対して $`\varphi, \psi`$ という記号ラベルを使っています（記号なんて、どうでもいいのだけど）。

自由関手が欠如したアドホック随伴系は次のような場合に使われます。

特定個別の“台対象と自由対象”が扱えれば十分なとき。
自由関手を完全に定義するのが困難なとき。
自由関手にあえて言及する必然性がないとき。
自由関手または部分的な自由関手を構成する中間段階として。

アドホック随伴系のアドホック単位

「随伴の自然なホムセット同型から単位自然変換へ」に書いたように、自然なホムセット同型があれば、そこから単位自然変換 $`\eta`$ を構成することができます。単位自然変換は次のような自然変換です。

$`\quad \eta :: \mrm{Id}_\cat{C} \twoto L*R : \cat{C} \to \cat{C} \In {\bf CAT}`$

単位自然変換の特定の成分 $`\eta_A`$ を定義するには次の公式を使います（「随伴の自然なホムセット同型から単位自然変換へ」参照）。

$`\quad \eta_A := \varphi_{A, L(A)}(\id_{L(A)})\;: A \to R( L(A) )\In \cat{C}`$

自由関手（＝左関手）が欠如していて、代わりに個別の自由対象 $`W`$ があるときなら、射（もはや自然変換の成分とは言えない）$`\eta_A`$ は次のように書けます。

$`\quad \eta_A := \varphi_{A, W}(\id_{W})\;: A \to R(W)\In \cat{C}`$

この $`\eta_A`$ の定義（自然変換 $`\eta`$ の定義ではない！）には、自由関手（＝左関手）が出てこないので、アドホック随伴系でも通用します。下付き $`A`$ を付けていると、自然変換の成分だと誤解を招きそうなので、一文字 $`\iota`$ にします。

$`\quad \iota : A \to R(W)\In \cat{C}\\
\text{i.e.}\\
\quad \iota \in \cat{C}(A, R(W))
`$

この $`\iota`$ をアドホック随伴系のアドホック単位〈ad-hoc unit〉と呼ぶことにします*3。アドホック単位は自然変換ではなくて、単一の射です。

アドホック単位 $`\iota`$ が重要なのは、射 $`\iota`$ により、転置 $`\varphi`$ が具体的に書き下せるからです。それを次節で説明します。

アドホック単位と転置

今までと同様に、自由関手（＝左関手）が欠如したアドホック随伴系が与えられた状況で話をします。アドホック随伴系の転置 $`\varphi`$ は、次のようなホムセット間の同型写像の族で、全体として自然変換になるのでした。$`R = U`$ （右＝忘却）としているで注意してください。

$`\quad \varphi_Y : \cat{D}(W, Y) \to \cat{C}(A, U(Y)) \In {\bf Set} \;\text{ natural in } Y \in |\cat{D}|\\
\text{i.e.}\\
\quad \varphi :: \cat{D}(W, \hyp) \twoto \cat{C}(A, U(\hyp)) : \cat{D} \to {\bf Set} \In {\bf CAT}\\
\text{i.e.}\\
\quad \varphi : \cat{D}(W, \hyp) \to \cat{C}(A, U(\hyp)) \In [\cat{D}, {\bf Set}]
`$

アドホック随伴系の定義から、自然変換 $`\varphi`$ は可逆で $`\varphi^{-1}`$ が存在します。逆自然変換が反転置でした。

さて、一時的に、$`G(\hyp) = \cat{C}(A, U(\hyp))`$ と置いて、共変バージョンの米田の補題（のインスタンス）を書いてみると：

$`\quad [\cat{D}, {\bf Set}](\cat{D}(W, \hyp), G) \cong G(W) \In {\bf Set}`$

この同型（左から右）は、米田写像〈Yoneda map〉 $`{\bf y} = {\bf y}[W, G]`$ で与えられます。

$`\quad {\bf y}: [\cat{D}, {\bf Set}](\cat{D}(W, \hyp), G) \to G(W) \In {\bf Set}\\
\quad {\bf y}^{-1}: G(W) \to [\cat{D}, {\bf Set}](\cat{D}(W, \hyp), G) \In {\bf Set}`$

$`{\bf y}`$ も $`{\bf y}^{-1}`$ も具体的な表示を持つので具体的な計算ができます。米田の補題と米田写像に関しては、以下の過去記事などを参照してください。

$`\alpha`$ と $`a`$ は以下のように相互対応しているとします。

$`\For \alpha \in [\cat{D}, {\bf Set}](\cat{D}(W, \hyp), G)\\
\quad {\bf y}(\alpha) = a \;\in G(W)\\
\For a \in G(W)\\
\quad {\bf y}^{-1}(a) = \alpha \;\in [\cat{D}, {\bf Set}](\cat{D}(W, \hyp), G)
`$

この前提で、$`\alpha, a`$ は次のような具体的な表示を持ちます。

$`\quad {\bf y}(\alpha) = a := \alpha_W(\id_W)\\
\:\\
\quad {\bf y}^{-1}(a) = \alpha\\
\For Y \in \cat{D}\\
\quad \alpha_Y : D(W, Y ) \to G(Y) \In {\bf Set}\\
\quad \For g \in D(W, Y )\\
\qquad \alpha_Y(g) := G(g)(a)
`$

$`G(g)(a)`$ を展開すれば：

$`\quad G(g)(a)\\
= \cat{C}(A, U(g))(a)\\
= U(g) \circ a
`$

この具体的な表示を $`\alpha = \varphi, a = \iota`$ の場合に具体化すれば：

$`\quad \varphi_Y(g) = U(g)\circ \iota`$

つまり、アドホック随伴系においては、転置 $`\varphi`$ とアドホック単位 $`\iota`$ は、次の等式で互いに規定しあうことになります。

$`\quad \varphi_Y(\hyp) = U(\hyp)\circ \iota \;\text{ for }Y \in |\cat{D}|\\
\quad \iota = \varphi_{W}(\id_W)
`$

そしてそれから

過去記事で、アドホック随伴系の自由対象が出てくる例は、「フリーモナド 1：自由で無料な木」にあります。

特定の関手 $`F\in |[{\bf Set}, {\bf Se}]|`$ に対して、忘却関手 $`\mathbb{U}`$ に関する $`F`$ 上の自由対象〈free object〉 $`M`$。

ここで、台対象 $`F`$ に対する自由対象 $`M`$ が出てきます*4。

今回のこの記事は、普遍性に関して書こうとしていたら長くなり過ぎたので、その一部を切り出したものです。したがって、アドホック随伴系は普遍性の議論に使う心づもりがあります。

[追記]普遍性に関する記事を書きました。

圏論の普遍性が難しい理由

[/追記]

*1:個人ルール、ローカルルールでは、理不尽にならないように注意しているつもりです。

*2:ストリング図内では、僕は自明圏として $`\unicode{x2606}`$ をよく使っています。

*3:「普遍〈universal〉」という言葉を使うのは、ここではやめておきます。「普遍」については別記事で話題にする予定です。[追記]書きました。→ 「圏論の普遍性が難しい理由」[/追記]

*4:単に事例が欲しいなら、通常の随伴系から左関手を取り除けばアドホック随伴系になります。

代数的な随伴系： 名付けの憂鬱