米田の補題は既に知られているとして、米田の補題を左カン拡張の枠組みで解釈できるでしょうか? できます。やってみます。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\twoto}{\Rightarrow }
\newcommand{\In}{\text{ in } }
%\newcommand{\Iff}{\Leftrightarrow }
\newcommand{\hyp}{\text{-} }
\newcommand{\op}{\mathrm{op} }
\newcommand{\id}{\mathrm{id} }
\require{color} % 緑色
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }%
\newcommand{\For}{\Keyword{For } }%
\newcommand{\Define}{\Keyword{Define } }%
\newcommand{\Where}{\Keyword{Where } }%
\newcommand{\Subject}{\Keyword{Subject } }%
`$
内容:
はじめに
表題のとおり、話題は米田の補題と左カン拡張なんですが、「米田の補題を確認しよう」よりは「カン拡張を事例で理解しよう」のほうが主要な目的です。カン拡張って分かりにくいので。
「それでもカン拡張の左右を忘れてしまう」に書いたように:
何の必然性もなく命名された「左」「右」を憶えるのは大変です。
「左」と「右」の二種類しかないのに憶えられないのは僕が記憶力悪すぎる、ってことではありますがね。
同じ過去記事の「関連する関手・自然変換の名前」のところに次のようにも書いています。
カン拡張が憶えにくいのは、構造としての構成素に役割り名が付いてないことも原因です。
「カン拡張の普遍性とは?」でも同様なことを言っていて:
構造/系と考えた左カン拡張では、ほとんどの構成素達に役割り名が与えられてません。結局、構造/系の構成素が匿名化/暗黙化されて、「そこは察しろ、悟れ」となります。カン拡張が分かりにくい理由かも知れません。
カン拡張を定義するための枠組み・舞台には、主役以外の登場人物もいるんだけど、匿名化/暗黙化されているので意識しにくいって事情です。意識しないと理解できないのに。
次節で、主役以外の登場人物と、そもそも主役って誰なの? を整理します。
右カン拡張とその周辺
「左」と「右」の二種類のカン拡張がありますが、右カン拡張から話をはじめます。
右カン拡張は「普遍性により」、あるいは「普遍構成法により」定義されます。この「普遍性」がけっこう分かりにくいという話は以下の過去記事でしました。
右カン拡張について言えば、「普遍性により」「普遍構成法により」は次のことを意味します。
- $`[\cat{D}, \cat{E}]`$ 上の前層 $`[\cat{C}, \cat{E}](K * \hyp, F)`$ の表現可能性の議論により
「関手の表現可能性と、要素の圏の終対象・始対象」で述べたように、表現可能性/余表現可能性の議論の代わりに、とある圏の終対象・始対象として右カン拡張/左カン拡張を定義することもできます。この場合の「普遍性/余普遍性」は、「終対象であること/始対象であること」を意味します。
ここでは、終対象として右カン拡張を定義する方法を前提にします。この前提のもとで、「カン拡張のために、柱の絵を描く」で使った絵(「それでもカン拡張の左右を忘れてしまう」にも再掲)をイメージすると、右カン拡張を定義するための登場人物の役割り名は次のように決めていいでしょう(「それでもカン拡張の左右を忘れてしまう // 関連する関手・自然変換の名前」から)。
- 形状関手: $`K:\cat{C} \to \cat{D}`$
- 標的圏〈ターゲット圏〉: $`\cat{E}`$
- 底面関手: $`F:\cat{C}\to \cat{E}`$
- 余底面関手: $`G:\cat{D}\to \cat{E}`$
- 柱体変換: $`\alpha :: K*G \Rightarrow F : \cat{C} \to \cat{E}`$
極限の場合は、柱体の代わりに、柱体が退化した錐体〈cone | 錐〉を考えます。(以下の $`{\bf I}`$ は、単一対象と恒等射だけの自明圏。)
- 錐体形状関手: $`K:\cat{C} \to {\bf I}`$ (自明な関手)
- 標的圏〈ターゲット圏〉: $`\cat{E}`$
- 底面関手: $`F:\cat{C}\to \cat{E}`$
- 頂点関手: $`G: {\bf I} \to \cat{E}`$ (ひとつの対象をポインティングするだけ)
- 錐体変換: $`\alpha :: K*G \Rightarrow F : \cat{C} \to \cat{E}`$
このネーミングの欠点は、特定描画法に基づく図形的なイメージが強すぎて、図形的イメージが不適切な場合に理解の障害になる可能性があることです。強すぎるイメージを緩和するために、柱体と余柱体のストリング図を併用するといいでしょう。以下は、柱体に対応するストリング図です。描画方向は上から下/左から右です。

ストリング図の描き方については次の記事にまとめてあります。
(「カン」とは限らない)右拡張〈right extension〉とは、圏 $`\cat{E}`$ 内に描かれた柱体(と呼ばれる構造)であり、右カン拡張は右拡張の圏の終対象のことです。したがって、右カン拡張も柱体(= 右拡張)の特別なものであり、柱体の構成素一式を備えています。
柱体の構成素一式のなかで、形状関手 $`K`$ 、ターゲット圏 $`\cat{E}`$ 、底面関手 $`F`$ は最初に固定されるので、終対象を識別するには、余底面関手と柱体変換のペア $`(R,\rho)`$ の情報でも十分です(他の情報は周知であるとの仮定のもとで)。
$`\quad R : \cat{D} \to \cat{E} \In {\bf CAT}\\
\quad \rho :: K*R \twoto F : \cat{C} \to \cat{E} \In {\bf CAT}
`$
通常、右カン拡張 $`\mrm{Ran}_K F`$ と書かれる関手は $`R`$ のことです。関手により、関手と自然変換のペアを代表しているとも言えます。次のような記号の乱用です。
$`\quad R = (R, \rho)`$
しかし、自然変換 $`\rho`$ は、関手 $`R`$ の情報をプロファイル(域と余域の仕様)として含んでいるので、次のように書くほうが適切でしょう。
$`\quad \rho = (R, \rho) \;: K*R \twoto F \In {\bf CAT}`$
あるいは:
$`\quad \rho = (R, \rho) \;: K*R \to F \In [\cat{C}, \cat{E}]`$
例えて言えば、“主役のクレジット”が間違っているようなもんです。右カン拡張(= 終対象である柱体)という構造の主役は自然変換 $`\rho`$ です。$`R`$ は $`\rho`$ に付随した情報です。
左カン拡張
左カン拡張は右カン拡張の双対なので、余柱体(= 左拡張)の圏の始対象として定義されます。余柱体を構成する各部〈構成素〉の呼び名は柱体とほとんど同じで、変更するのは「柱体変換」だけです。
- 形状関手: $`K:\cat{C} \to \cat{D}`$
- 標的圏〈ターゲット圏〉: $`\cat{E}`$
- 底面関手: $`F:\cat{C}\to \cat{E}`$
- 余底面関手: $`G:\cat{D}\to \cat{E}`$
- 余柱体変換: $`\beta :: F \Rightarrow K*G : \cat{C} \to \cat{E}`$
双対でひっくり返る矢印(2-射の二重矢印)は、 $`K*G \Rightarrow F`$ だけです。言い方を変えると、関手圏 $`[\cat{C}, \cat{E}]`$ のなかでひっくり返し〈reversal | reversing〉が発生します。
固定した $`K, F`$ に対する余柱体の圏を $`\mrm{Cocyl}_{K, F}`$ と書くことにします。余柱体の圏 $`\mrm{Cocyl}_{K, F}`$ の射とは何かというと、ひとつの自然変換と自然変換のあいだの等式で記述されるのですが、一般的な射ではなくて、始対象からの唯一の射について説明します。
$`K, F`$ は(当然に $`\cat{C},\cat{D}, \cat{E}`$ も)固定されているとして、余柱体(= 左拡張)の圏の始対象を
$`\quad \lambda = (L, \lambda) \;\in |\mrm{Cocyl}_{K, F}|\\
\text{i.e.}\\
\quad \lambda = (L, \lambda) : F \to K*L \In [\cat{C}, \cat{E}]\\
\text{i.e.}\\
\quad \lambda = (L, \lambda) :: F \twoto K*L \In {\bf CAT}
`$
とします。任意の余柱体を
$`\quad \beta = (G, \beta) \;\in |\mrm{Cocyl}_{K, F}|\\
\text{i.e.}\\
\quad \beta = (G, \beta) : F \to K*G \In [\cat{C}, \cat{E}]\\
\text{i.e.}\\
\quad \beta = (G, \beta) :: F \twoto K*G \In {\bf CAT}
`$
とします。
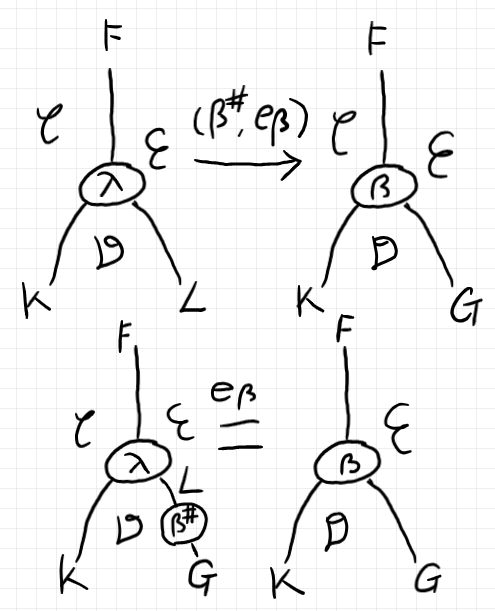
一般に、余柱体のあいだの射は、自然変換 $`\tau`$ と等式 $`e`$ のペア $`(\tau, e)`$ で決まりますが、始対象からの射は $`\beta`$ から一意的に決まってしまうので、その唯一の射を $`(\beta^\sharp, e_\beta)`$ とします。
$`\quad (\beta^\sharp, e_\beta) : (L, \lambda) \to (G, \beta) \In \mrm{Cocyl}_{K, F}\\
\Where\\
\quad \beta^\sharp :: L \twoto G \In {\bf CAT}\\
\quad e_\beta ::: \lambda; (K * \beta^\sharp) = \alpha :: F \twoto K*G \In {\bf CAT}
`$
ストリング図で描くと分かりやすいでしょう(下)。
米田の補題
米田の補題を次の形で書きます。
$`\quad [\cat{C}^\op, {\bf Set}](よ[A], F) \cong F(A)`$
ここで、$`よ[\hyp]`$ は米田埋め込み〈Yoneda embedding〉です。
$`\quad よ : \cat{C} \to [\cat{C}^\op, {\bf Set}]\\
\For A \in |\cat{C}|\\
\quad よ[A] = \cat{C}(\hyp, A)\;: \cat{C}^\op \to {\bf Set} \In {\bf CAT}
`$
米田の補題を、左カン拡張の一般的フレームワークに載せるには、一般論で出てきた記号ラベルを“事例である米田の補題の特殊ケース”の記号ラベルに当てはめます。変数(記号ラベル)を具体化するパターンマッチングをやるわけです。一般論を事例に適用する場合は、常にこのテのパターンマッチングをします。
以下に、記号ラベルの当てはめ〈パターンマッチング〉を一覧表で示します。
| $`\text{一般論}`$ | $`\text{事例}`$ | $`\text{事例への備考}`$ |
|---|---|---|
| $`\cat{C}`$ | $`{\bf I}`$ | 自明圏〈単位圏〉 |
| $`\cat{D}`$ | $`\cat{C}`$ | 一般的な圏 |
| $`\cat{E}`$ | $`{\bf Set}`$ | 集合圏 |
| $`K`$ | $`A`$ | 対象をポインティングする関手 |
| $`F`$ | $`{\bf 1}`$ | 対象をポインティングする関手 |
| $`G`$ | $`F`$ | 一般的な関手 |
| $`\beta`$ | $`x`$ | 集合(前層の値)の要素 |
| $`L`$ | $`よ[A]`$ | 米田埋め込みの値 |
| $`\lambda`$ | $`\id_A`$ | 集合(ホムセット)の要素 |
すべての登場人物〈構成素〉を、小さくないかも知れない圏達の2-圏 $`{\bf CAT}`$ という舞台に乗せて論じることになります。圏の対象や集合の要素も $`{\bf CAT}`$ のk-射とみなします。この点を以下に説明しておきます。
圏の対象 $`A\in |\cat{C}|`$ があると、次のような関手を定義できます。$`\Subject`$で、定義すべきモノを宣言してから実際の定義を続けます。
$`\Subject A^\sim : {\bf I} \to \cat{C} \In {\bf CAT}\\
\quad \For 0 \in |{\bf I}| \\
\quad \Define A^\sim(0) := A\; \in |\cat{C}|\\
\quad \For \id_0: 0 \to 0 \In {\bf I} \\
\quad \Define A^\sim(\id_0) := (\id_A\ : A^\sim(0) \to A^\sim(0) \In \cat{C})
`$
対象 $`A`$ と関手 $`A^\sim`$ を同一視します。
$`A \in |{\bf Set}|`$ で $`a\in A`$ のとき、要素 $`a`$ は次のようにして自然変換だとみなします。
$`\Subject {a^\sim}^\sim :: {\bf 1}^\sim \twoto A^\sim : {\bf I} \to {\bf Set} \In {\bf CAT}\\
\quad \For 0 \in |{\bf I}| \\
\quad \Define {{a^\sim}^\sim}_0 := (a^\sim : {\bf 1} \to A \In {\bf Set})\\
\quad \Where a^\sim := ({\bf 1}\ni 0 \mapsto a \in A)
`$
$`{a^\sim}^\sim`$ は実際に自然変換になります。要素 $`a`$ と自然変換 $`{a^\sim}^\sim`$ を同一視します。
上記のような同一視を僕は格上げ〈promote | bump up〉と呼んでいますが、格上げについては、「圏論の随伴をちゃんと抑えよう: お絵描き完全解説 // 対象と射の格上げ」に説明があります。
さて、米田の補題によれば、集合の要素 $`x\in F(A)`$ に対して、自然変換が一意的に決まります。その自然変換を $`x^\sharp`$ とします。
$`\quad x^\sharp :: よ[A] \twoto F : \cat{C}^\op \to {\bf Set} \In {\bf CAT}`$
$`x^\sharp \longleftrightarrow x`$ という一対一対応は、米田同型(米田写像と逆米田写像)によって与えられます。米田同型のストリング図による解釈は次の記事にあります。
これで準備はできました。左カン拡張に対して描いたストリング図と同様なストリング図を、米田の補題の状況に対して描いてみます。
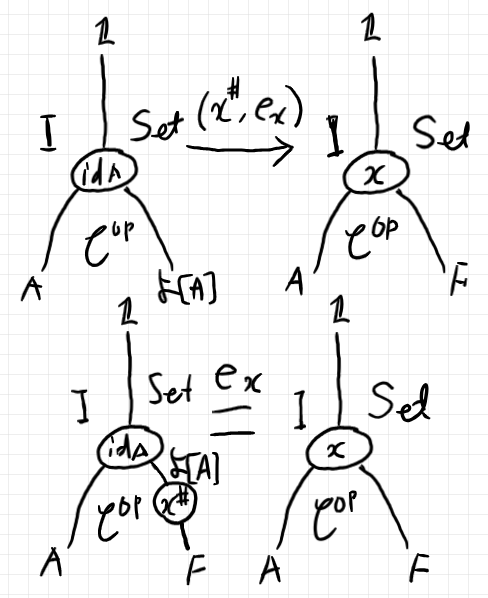
このストリング図がすべてを表しています。米田の補題の主張は、左カン拡張のフレームワークのなかで解釈できます。