ローヴェア・セオリーとその周辺 - 檜山正幸のキマイラ飼育記 (はてなBlog)

ローヴェア〈William Lawvere〉は、彼の学位論文で「セオリー」という概念を導入しました。現在、ローヴェアのセオリーに対する色々な呼び名がありますが（「用語のバリエーション記述のための正規表現 // ウンザリする例」参照）、ここではローヴェア・セオリー〈Lawvere theory〉と呼ぶことにします。

ローヴェアは、ローヴェア・セオリーを対象物とした議論をおこなったので、ローヴェア・セオリーのセオリー〈理論〉を展開したことになります。概念的事物に「セオリー」というネーミングをしたことで、それについて語るのがややこしくなってしまいました。

ローヴェア・セオリー以前にセオリーと呼ばれていたモノもあり、それらも一緒に話題にすると、さらに混乱しがちです。ある程度は形式化したスタイルを使わないと、どうにも収拾がつかないですね。

という事情で、ある程度は形式化したスタイルでローヴェア・セオリーについて紹介します。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\u}[1]{\underline{#1}}
%\newcommand{\o}[1]{\overline{#1}}
\newcommand{\hyp}{\text{－} }
\newcommand{\id}{\mathrm{id}}
\newcommand{\In}{\text{ in } }
%\newcommand{\twoto}{\Rightarrow }
\newcommand{\dimU}[2]{{#1}\!\updownarrow^{#2}}
\require{color} % 緑色
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }%
\newcommand{\For}{\Keyword{For } }%
\newcommand{\Define}{\Keyword{Define } }%
\newcommand{\Subject}{\Keyword{Subject } }%
%\newcommand{\Where}{\Keyword{Where } }
%\newcommand{\And}{\Keyword{And } }
%\newcommand{\Let}{\Keyword{Let } }
`$

内容：

呼び名の約束
全体像
デカルト・モノイド圏
単元生成デカルト厳密モノイド小圏
ローヴェア・セオリーのモデル
等式的代数指標と複圏
複圏のモノイド圏への表現
ローヴェア圏と単彩的複圏
おわりに

関連する過去記事：

呼び名の約束

内容的な説明をする前に、「セオリー」で混乱してしまうことを回避するために、次の約束をします。

ローヴェア・セオリーはある種の圏なので、ローヴェア圏〈Lawvere category〉とも呼びます。「ローヴェア圏〈ローヴェア・セオリー〉」とか「ローヴェア・セオリー〈ローヴェア圏〉」とかの書き方も使います。
ローヴェア圏は、それ以前から論理や普遍代数で使われていた等式的代数指標〈equational algebraic signature〉を置き換える概念です。等式的代数指標を、等式的セオリー〈equational theory〉とか代数セオリー〈algebraic theory〉とも呼びます。が、ここでは指標をセオリーと呼ぶことはしません。
等式的代数指標があると、それをもとに、同値関係を備えた複圏〈multicategory〉とその商複圏〈quotient multicategory〉を作れます。この複圏／商複圏もセオリーと呼びます。が、ここでは複圏／商複圏をセオリーと呼ぶことはしません。
地の文のなかで、国語辞書的意味で「セオリー」を使いたいときは、漢字で「理論」と書きます。例えば、「ローヴェア・セオリーの理論」のように。

結局、「セオリー」はローヴェア圏の意味だけに使い、他の概念は「等式的代数指標」「複圏」「商複圏」という呼び名にします。

「代数〈algebra〉」も意味が拡散してしまって使いにくい言葉です。ローヴェア・セオリーの文脈で出てくる「ローヴェア代数」あるいは単に「代数」も使わないことにします。代わりに、（ローヴェア・セオリーの）「ローヴェア・モデル〈Lawvere model〉」あるいは単に「モデル〈model〉」を使います。オペラッド上の代数〈algebra over an operad〉も、代数ではなくて複圏の表現〈multicategory representation〉という呼び名を使います。なお、「複圏」と「オペラッド」のゴチャゴチャした事情は「オペラッドの話」に書いてあります。

それと、モノイド関手に付ける形容詞「タイト〈tight〉」は「強〈strong〉」と同義ですが、強度〈strength〉とゴッチャになってしまって困るので「強」も使いません。

全体像

議論の全体像を示すために、一応、次の図式を出します。

$`\xymatrix@C+2.5pc@R+1pc{
{\bf EqAlgSig} \ar[d]^-{\mrm{SigToMulticat}}
\\
{\bf MonocMulticat} \ar[r]^-{\mrm{MulticatRep}[\hyp]({\bf Set})}
\ar@/^1pc/[d]^{\mrm{MulticatToCat}}
& {\bf CAT} \ar@{=}[d]
\\
{\bf LawTh} \ar[r]_-{\mrm{LawMod}[\hyp]({\bf Set})}
\ar@/^1pc/[u]^{\mrm{CatToMulticat}}
& {\bf CAT}
}`$

「一応」と言ったのは、この図式を正確に説明するのが難しいからです。図式内に $`{\bf CAT}`$（小さくない圏も含む圏達の2-圏）が出現するので、図式が描かれている場所（環境）は $`\mathbb{2CAT}`$（大きな圏達からなるとても大きな2-圏である $`{\bf CAT}`$ を対象として含むようなサイズの2-圏達の3-圏）ということになります。矢印は、2-関手〈(2, 0)-変換手〉（「変換手2-圏の代数構造とストリング図表現」参照）となります。大規模高次〈large-size higher-dimensional〉な世界に描かれている図式です。

という事情なので、上の図式は雰囲気的なポンチ絵のたぐいとして捉えてください。図式に出てくる太字の名前は圏または2-圏です。

$`{\bf EqAlgSig}`$ ：等式的代数指標の圏。射は、指標と指標を等式的法則も含めて対応付ける写像（のようなもの）。射を定義するのは難しいです。
$`{\bf MonocMulticat}`$ ：単彩的複圏〈monochrome multicategory〉（「オペラッドの話」参照）を対象として、複関手（「回路代数とグラフ置換モナド // スケマティック系とオペラッド」参照）を射とする圏。複関手のあいだの自然変換を考えれば2-圏にもなります。
$`{\bf LawTh}`$ ：ローヴェア・セオリー（本記事の主題）を対象として、ローヴェア・セオリーのあいだの準同型射を射とする圏。本来は2-圏だが、2-射が等式に退化しています。
$`{\bf CAT}`$ ：必ずしも小さくない圏も対象として、関手を1-射、自然変換を2-射とする厳密2-圏。

上の図式が可換か？と言うと、等式が成立するという意味での厳密な可換性はありません。しかし、図式が描かれている場所が高次圏なので、2-関手のあいだの同型・同値などのゆるい等式の概念があります。ゆるい等式の意味では可換です。

図式に出現する圏／2-圏達のあいだを結ぶ関手についてはこの後で説明します。

デカルト・モノイド圏

ローヴェア・セオリー〈ローヴェア圏〉の説明だと、ほとんど常に有限積を持つ圏〈category with finite product | finite product category〉という概念が出てきますが、これは、現在の一般的な言葉ではデカルト・モノイド圏〈Cartesian monoidal category〉（圏の直積がモノイド積として与えられる圏）です。ここでは、原典に忠実であるよりポピュラーであることを優先して、「有限積」ではなくて「デカルト・モノイド積〈Cartesian monoidal product〉」あるいは単に「デカルト積〈Cartesian product〉」を使います。

デカルト・モノイド圏の定義も幾つかの流儀がありますが、対称モノイド圏 $`(\cat{C}, \otimes, I, \alpha, \lambda, \rho, \sigma)`$ の構造に加えて、コピー射〈余対角射〉の族 $`\Delta_A`$ と削除射〈破棄射〉の族 $`!_A`$ があり、これらの族がどちらも自然変換になっていることを要求するのが便利です。この流儀によるデカルト・モノイド圏は次のように書きます。

$`\quad (\cat{C}, \otimes, I, \alpha, \lambda, \rho, \sigma, \Delta, !)`$

長たらしいので、適宜省略します。例えば：

$`\quad (\cat{C}, \otimes, I, \Delta, !)`$

デカルト構造と台圏〈underlying category〉を区別して、記号をデカルトっぽくすると：

$`\quad \cat{C} = (\u{\cat{C}}, \times, {\bf 1}, \Delta, !)`$

$`{\bf CartMonCAT}`$ を、必ずしも小さくないデカルト・モノイド圏達を対象とする2-圏とします。この2-圏のk-射は次のようです。

0-射：必ずしも小さくないデカルト・モノイド圏
1-射：デカルト構造を保つタイト対称モノイド関手（すぐ下に説明）
2-射：対称モノイド自然変換

デカルト・モノイド圏は対称モノイド圏なので、そのあいだの1-射（関手）も、1-射のあいだの2-射（自然変換）も、対称モノイド圏に対する関手／自然変換をベースにして考えます。0-射〈対象〉の定義は既に述べた通りですが、1-射は明らかではありません。1-射の定義は意外に難しく、一意的に決まるものではありません。そのことは以下の過去記事に書いています。

これらの過去記事は書きっぱなしで追加修正はしてないので、右往左往している印象があるかも知れません。過去記事を書いた当時は「片方向だけラックスな定義」にこだわっていたのです。が、今回の目的では片方向だけラックスである必要がないので、1-射はタイトな（ラクセイターが可逆でラックスかつ反ラックスな）対称モノイド関手です。デカルト構造の保存は、コピー射・削除射が、反ラックス・モノイド関手と協調することです。

今述べた1-射の定義は、「デカルト・モノイド関手は色々」において次のように書いたものです。

例えば、$`F = (\u{F}, \nu, \iota):\cat{C} \to \cat{D}`$ がラックス・モノイド関手だとして、$`\nu, \iota`$ がそれぞれ規準的な $`\delta, \tau`$ の逆だと定義するのもアリはアリです（使いにくいですが）。

「使いにくい」と書いてますが、今回の目的では問題ありません。過去記事を読み直さなくてもいいように、1-射の定義を以下に簡単にまとめます。

まず、一般的なモノイド関手／モノイド自然変換、対称モノイド関手／対称モノイド自然変換については、「この2つのミニマムな解説はほんとに便利だ」で紹介したバエズの"Should know"などで確認してください。

ここから先は、デカルト・モノイド圏 $`\cat{C}`$ と $`\cat{D}`$ のあいだのデカルト・モノイド関手（$`
{\bf CartMonCAT}`$ の1-射）がどんなものかを見ていきます。

$`F = (\u{F}, \nu, \iota)`$ と $`F' = (\u{F'}, \delta, \tau)`$ は、同じ台関手 $`\u{F} = \u{F'}\, :\u{\cat{C}} \to \u{\cat{D}}`$ に載ったラックス・モノイド関手と反ラックス・モノイド関手だとします。この書き方と意味は「デカルト・モノイド圏のあいだの関手、そして自然変換」と同じです。ラックス・モノイド関手のラクセイター $`\nu, \iota`$ が可逆で、逆自然変換を次のように置きます。

$`\quad \delta := \nu^{-1},\; \tau := \iota^{-1}`$

こうして与えられた $`(\u{F}, \delta, \iota)`$ は反ラックス・モノイド関手となります。つまり、ラックス・モノイド関手 $`F = (\u{F}, \nu, \iota)`$ と反ラックス・モノイド関手 $`F' = (\u{F'}, \delta, \tau)`$ （$`\u{F} = \u{F'}`$）が、自然変換の逆によって互いに鏡像のような関係にあります。そのような状況を仮定します。

ここからは絵で説明します（テキストだとめんどくさいんで）。以下は、描画方向は上から下だとして、ラクセイター $`\delta = \nu^{-1}, \, \tau = \iota^{-1}`$ を表すストライプだとします（ストライプについては「ストリング図とストライプ図」やそこから参照されている過去記事をみてください）。ストライプの中身（圏 $`\cat{C}`$ の状況）は描いてません。

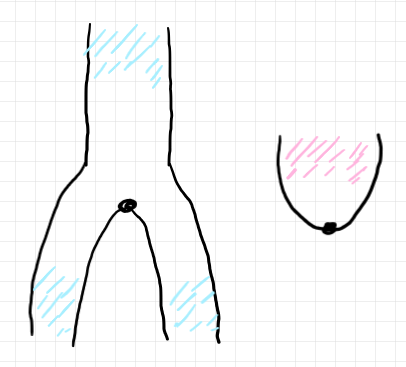
これらのラクセイター $`\delta, \tau`$ は、デカルト圏の構造射であるコピー射／削除射と次の関係があるとします。

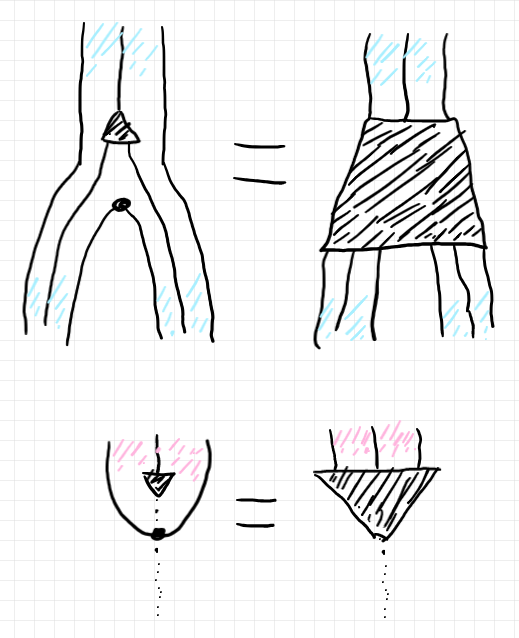
ここで、上向きの黒い三角、または黒い台形はコピー射です。下向きの黒い三角は削除射です。この等式の成立が、コピー射・削除射が、反ラックス・モノイド関手と協調することの意味です。

単元生成デカルト厳密モノイド小圏

ローヴェア圏〈ローヴェア・セオリー〉は、特殊なデカルト・モノイド圏です。非常に特殊だと言っていいでしょう。その特殊性は：

小さい圏である。
モノイド圏として厳密モノイド圏である。デカルト積は厳密に（等式により）結合的かつ単位的な演算になっている。
対象の集合は可算集合（$`{\bf N}`$ と同型）である。
それだけでなくて、対象の集合上のモノイド構造が自然数の足し算モノイドと同型になる。

これらの特徴を持つ圏は、単元生成デカルト厳密モノイド小圏と呼べます。「ローヴェア圏」は、この長たらしい名前の別名です。

ローヴェア圏達の圏を順番に構成していきましょう。まず $`{\bf CartStrMonCat}^\mrm{str}`$ を次のような2-圏だとします。

0-射〈対象〉は、デカルト厳密モノイド小圏。モノイド圏の結合律子〈associator〉、単位律子〈unitor〉は等式。
1-射は、デカルト構造を保つ厳密対称モノイド関手。ラクセイターは等式。
2-射は、1-射のあいだの対称モノイド自然変換。

ローヴェア圏は、（忘却関手を経由して）2-圏 $`{\bf CartStrMonCat}^\mrm{str}`$ の対象とみなせますが、さらに追加の構造・条件があります -- ローヴェア圏の対象上のモノイド構造が自然数の足し算構造と同じなので、その同型を与える写像を添えるのです。

デカルト厳密モノイド小圏 $`\cat{C}`$ と、写像 $`e : {\bf N} \to |\cat{C}|`$ の組 $`(\cat{C}, e)`$ が以下の条件を満たすとき、ローヴェア圏〈Lawvere category〉と呼びます。

$`e`$ は、モノイド $`({\bf N}, +, 0)`$ とモノイド $`(|\cat{C}|, \times, {\bf 1})`$ のあいだのモノイド同型写像である。

モノイド同型写像は、可逆なモノイド準同型写像です。モノイド準同型写像であるとは次が成り立つことです。

$`\For n, m \in {\bf N}\\
\quad e(n + m)= e(n)\times e(m) \In |\cat{C}|\\
\quad e(0) = {\bf 1} \;\in |\cat{C}|
`$

$`\cat{C}`$ のすべての対象は、$`e(1)`$ をデカルト積の意味で累乗（0乗もあり）して得られます。その意味で“単元生成”と形容したのです。$`\cat{C}`$ は厳密モノイド圏なので、$`e(1)^n`$ はup-to-isoではなくて、確定的にひとつに決まります。対象は自然数と完全に同一視できます。$`|\cat{C}| = {\bf N}`$ と考えたほうがスッキリするくらいです。

ローヴェア圏を $`\cat{L}`$ として、$`\cat{L} = (\u{\cat{L}}, e^\cat{L})`$ のように書きます。$`\u{\cat{L}}`$ は、ローヴェア圏の台となるデカルト厳密モノイド小圏です。

2つのローヴェア圏 $`\cat{L}, \cat{M}`$ のあいだの準同型射〈homomorphism〉は、台圏のあいだのデカルト構造を保つ厳密対称モノイド関手 $`F`$ であって、対象パート $`F_\mrm{obj}`$ が次の図式を可換にするものです。

$`\require{AMScd}
\quad \begin{CD}
|\u{\cat{L}}| @>{ F_\mrm{obj}}>> |\u{\cat{M}}|\\
@A{e^\cat{L}}AA @AA{e^\cat{M}}A \\
{\bf N} @= {\bf N}
\end{CD}\\
\quad \text{commutative in }{\bf Set}
`$

ローヴェア圏〈ローヴェア・セオリー〉を対象として、そのあいだの準同型射を射とする圏を $`{\bf LawTh}`$ とします。$`{\bf LawTh}`$ の対象は圏なので、自然変換を2-射とする2-圏に仕立てられますが、ローヴェア圏の特徴から、2-射は等式に退化してしまいます。なので、$`{\bf LawTh}`$ は名目上2-圏、事実上1-圏です。

$`{\bf LawTh}`$ は、2-圏 $`{\bf CartStrMonCat}^\mrm{str}`$ の部分2-圏ではありませんが、忘却関手は持ちます。

$`\quad U: {\bf LawTh} \to {\bf CartStrMonCat}^\mrm{str} \In {\bf 2CAT}`$

事実上1-圏なので、次のように考えても同じです。（$`\dimU{\hyp}{1}`$ については「圏の次元調整」参照。）

$`\quad U: \dimU{{\bf LawTh}}{1} \to \dimU{ {\bf CartStrMonCat}^\mrm{str} }{1} \In {\bf CAT}`$

次のような2-圏の包含の系列があります。

$`\quad {\bf CartStrMonCat}^\mrm{str}\subset {\bf CartMonCat} \subset {\bf CartMonCAT} \In \mathbb{2CAT}`$

この系列をたどることにより、ローヴェア圏〈ローヴェア・セオリー〉の圏（あるいは2-圏）$`{\bf LawTh}`$ は次の忘却関手を持つと考えられます。

$`\quad U: {\bf LawTh} \to {\bf CartMonCAT} \In \mathbb{2CAT}`$

[補足]
ローヴェア圏〈ローヴェア・セオリー〉の定義として、有限集合の圏 $`{\bf FinSet}`$ の標準骨格〈{standard | canonical} skeleton〉の反対圏からの identity-on-objects な埋め込み関手を備えた小さな圏というものがあります。そのような定義は、この記事の定義と同値です。

ローヴェア圏 $`\cat{L}`$ には厳密なデカルト・モノイド構造が載っているので、それを使うと当該の identity-on-objects な埋め込み関手を一意的に構成できます。
[/補足]

ローヴェア・セオリーのモデル

ひとつのローヴェア・セオリー〈ローヴェア圏〉$`\cat{L} \in |{\bf LawTh}|`$ を選ぶと、それに対してモデルの圏を構成できます。モデルの圏を構成するには、ターゲット圏〈target category〉であるデカルト・モノイド圏が必要です。最もよく使われるターゲット圏は、直積でデカルト・モノイド圏とみなした集合圏 $`{\bf Set} = ({\bf Set}, \times, {\bf 1})`$ （記号の乱用）です。

ローヴェア圏 $`\cat{L}`$ のモデル $`M`$ とは、デカルト厳密モノイド小圏 $`\u{\cat{L}} = U(\cat{L})`$ からターゲット圏（デカルトモノイド圏）へのデカルト・モノイド関手です。ここでのデカルト・モノイド関手とは、2-圏 $`{\bf CartMonCAT}`$ の1-射のことです。ターゲット圏が集合圏なら次のようです。

$`\quad M : \u{\cat{L}} \to {\bf Set} \In {\bf CartMonCat}`$

もうひとつのモデル $`M'`$ があるとき、$`M`$ から $`M'`$ への準同型射とは、“タイト対称モノイド関手としてのモデル” $`M, M'`$ のあいだの対称モノイド自然変換です。

これはつまり、ローヴェア圏 $`\cat{L}`$ のモデル達の圏は、2-圏 $`{\bf CartMonCAT}`$ のホム圏として与えられる、ということです。したがって、モデル〈ローヴェア・モデル〉の圏は次のような定義になります。

$`\quad \mrm{LawMod}[\cat{L}]({\bf Set}) := {\bf CartMonCAT}(U(\cat{L}), {\bf Set}) \;\in |{\bf CAT}|`$

実は、モデルの圏の構成は、Diag構成（「Diag構成：圏論的構成法の包括的フレームワークとして」）の事例です。Diag構成との関係は：

$`\quad \mrm{LawMod}[\cat{L}]({\bf Set}) = {\bf CartMonCAT}\text{-}\mrm{Diag}^{ {\bf LawTh}, U}[\cat{L}]({\bf Set})`$

ターゲット圏は集合圏のままで、色々なローヴェア・セオリーを考えるならば、

$`\quad \mrm{LawMod}[\hyp]({\bf Set}) : \dimU{\bf LawTh}{1} \to \dimU{\bf CAT}{1} \In \mathbb{CAT}`$

同一のローヴェア・セオリーに対してターゲット圏を変えるならば、

$`\quad \mrm{LawMod}[\cat{L}](\hyp) : \dimU{ {\bf CartMonCAT} }{1} \to \dimU{\bf CAT}{1} \In \mathbb{CAT}`$

ローヴェア・セオリーとターゲット圏の両方を変化させるなら次のような関手になります。

$`\quad \mrm{LawMod}[\hyp](\hyp) : \dimU{ {\bf CartMonCAT} }{1} \to [\dimU{\bf LawTh}{1}, \dimU{\bf CAT}{1}]\In \mathbb{CAT}`$

2-圏ベースで（$`\mathbb{2CAT}`$ のなかで）考えるほうがベターでしょうが、複雑になります。

モデルが関手で、モデルのあいだの射が自然変換になることから、ローヴェア・モデルは関手モデルと呼ばれ、関手モデルを使う方法は関手意味論〈functorial semantics〉と呼ばれます。関手意味論については、比較的最近の記事でも触れています。

「代数」への三種のアプローチと回路代数

等式的代数指標と複圏

ローヴェアがローヴェア・セオリーを考案した動機・目的は、等式的代数指標を圏で置き換えることでしょう。等式的代数指標は、線形代数に例えるならベクトル空間の基底のようなものです。基底を使って成分〈座標〉計算する手法から、ベクトル空間自体を相手にする座標非依存な〈coordinate-free〉方法への進化が、等式的代数指標からローヴェア圏への進化に対応します。

一例として、群の等式的代数指標〈equational algebraic signature〉は次のようになります。

signature Group {
  sort U

  operation m : U×U → U
  operation e : 1 → U
  operation s : U → U

  variable x, y, z
  equation assoc :: m(m(x, y), z) = m(x, m(y, z))
  equation lunit :: m(e, x) = x
  equation runit :: m(x, e) = x
  equation linv :: m(r(x), x) = e
  equation rinv :: m(x, r(x)) = e
}

この指標では、ソート〈型 | 色〉が U だけしかないので、単ソート指標〈single-sort signature〉といいます。単ソート指標では、ソートの名前は何でもいいので、必要な情報は各演算子記号の項数だけです。「オペラッドの話」の事例のように、基本演算子記号から組み立てた式〈項〉をすべて考えると複圏〈オペラッド〉を生成できます。

群の指標 Group の基本演算子記号 m, e, r から生成された複圏〈オペラッド〉を $`\widetilde{\cat{G}}`$ とすると、オペセット $`\widetilde{\cat{G}}(n)`$ は、群で解釈可能な$`n`$項の式の集合になります。オペラッド結合は代入です。各オペセットには、指標の等式的法則〈equational laws〉により定義される同値関係が入ります。組み合わせ的議論がめんどうですが、複圏構造と同値関係が整合することが示せます。

複圏 $`\widetilde{\cat{G}}`$ の各オペセットを指標の等式的法則から決まる同値関係により商集合を作ります。複圏構造と同値関係が整合することから、商集合をオペセットとする複圏を定義可能です。商複圏〈商オペラッド〉を $`\cat{G}`$ とします。

ここまでに、以下の構造が登場しました。

群の等式的代数指標
指標の等式的法則は考えずに、指標の演算子記号だけから作った無法則複圏〈lawless multicategory〉$`\widetilde{\cat{G}}`$
指標の等式法則から決まる同値関係によりオペセットごとに商集合を作った商複圏〈quotient multicategory〉$`{\cat{G}}`$

最初の章で注意したように、上記箇条書きのどれも「セオリー」と呼ぶことがあります。ここでは「セオリー」は使わず、等式的代数指標 $`\Sigma`$ に対する商複圏を $`\mrm{SigToMulticat}(\Sigma)`$ と表すことにします。$`\mrm{SigToMulticat}(\Sigma)`$ は、単ソート指標で定義される式〈項〉の計算を表す代数系です。

[補足]
ここでは、等式的法則がオペセット（記号的項の集合）上の同値関係を定義するとして、その同値関係で商をとりました。しかし、必ずしも商をとる必要はありません。各オペセットに同値関係が載っている状態でそのまま扱うということです。

同値関係が載った集合は亜集合〈setoid〉といいます。オペセットが亜集合である複圏〈オペラッド〉は、亜集合の対称モノイド圏 $`{\bf Setoid}`$ で豊穣化された複圏です。商をとらないとは、豊穣複圏として扱うことになります。

等式的代数指標の基本演算子定義で複圏の複射が定義されて、等式的法則がオペセット内の2-射を定義することになります。別な言い方をすれば、等式的法則達は2-射の生成系となっています。

等式に対しては等式的推論ができます。等式が2-射だとすると、等式的推論は、2-射を“色”とする色彩的複圏〈色付きオペラッド〉の複射ともみなせます。圏と複圏の構造が何階層にも積み重なっている状況があるようです（「演繹系とオペラッド」も参照）。
[/補足]

複圏のモノイド圏への表現

必ずしも単彩〈monochrome〉でなくても、一般的な色彩的複圏〈色付きオペラッド〉に対して表現を定義できます。が、ここでは単彩的複圏〈単色オペラッド〉の表現に限定します。単彩的複圏の定義は、「オペラッドの話」に出ている $`\cat{O}`$ という名前の事例を参照してください。

ここでは、単彩的複圏を $`\cat{M}`$ とします。自然数 $`n`$ に対して、複ホムセット〈オペセット〉は $`\cat{M}(n)`$ です。これは、$`\cat{M}(n, 1)`$ と書いてもかまいません。複圏の単純結合は、図式順は '$`;_k`$' 、反図式順は '$`\circ_k`$' という記号を使います。恒等は $`\mrm{i}`$ とします。

$`\cat{V} = (\cat{V}, \otimes, I)`$ （記号の乱用）を対称モノイド圏とします。任意の対象 $`X \in |\cat{V}|`$ に対して、“$`X`$ の$`n`$乗”は次のように定義します。“$`X`$ の$`0`$乗”はモノイド単位対象 $`I`$ です。

$`\quad X^{\otimes n} := X\otimes \cdots \otimes X \;(n \text{ times})\:\in |\cat{V}|`$

単彩的複圏 $`M`$ のターゲット圏 $`\cat{V}`$ への表現〈representation〉 $`F`$ は次のモノからなります。

$`\cat{V}`$ の対象 $`R`$ （表現対象〈representation object〉 | 台対象〈underlying object〉）
自然数 $`n`$ ごとに、写像 $`F_n : \cat{M}(n) \to \cat{V}(R^{\otimes n}, R)\In {\bf Set}`$

$`F_n`$ 達は、複圏の単純結合を保つ必要があります。これは関手性〈functoriality〉と似た性質で複関手性〈multifunctoriality〉です。とはいえ、$`\cat{V}`$ は複圏〈オペラッド〉ではないので、複結合〈オペラッド結合〉としての単純結合は（最初からは）持っていません。次のように定義します。（以下、$`\Subject`$で、定義すべきモノを宣言してから実際の定義を続けます。）

$`\Subject (;_k) : \cat{V}(R^{\otimes n}, R) \times \cat{V}(R^{\otimes m}, R) \to \cat{V}(R^{\otimes (n + m - 1)}, R) \In {\bf Set} \\
\For f \in \cat{V}(R^{\otimes n}, R), g \in \cat{V}(R^{\otimes m}, R)\\
\quad f\,;_k g := (\id_R\otimes \cdots \otimes f \otimes \cdots\otimes \id_R) ; g \;\in \cat{V}(R^{\otimes (n + m - 1)}, R)
`$

ちょっと雑な定義ですが、言いたいことは伝わるでしょう。この定義により、$`\cat{V}(R^{\otimes n}, R)`$ 達は複結合〈オペラッド結合〉としての単純結合 $`(;_k)`$ を備えたので、“単純結合を保つ”ことを次のように記述できます。

$`\For x \in \cat{M}(n),\; y \in \cat{M}(m)\\
\For 1 \le k \le m\\
\quad F_{n + m - 1}(x \,;_k y) = F_{n}(x)\,;_k F_{m}(y) \In\cat{V}(R^{\otimes (n + m - 1)}, R)
`$

あ、そうそう、恒等も保つ必要がありました。

$`\For n \in {\bf N}\\
\quad F_{1}(\mrm{i}) = \id_R \In\cat{V}(R^{\otimes 1}, R)
`$

一般に、対称モノイド圏 $`\cat{V}`$ から標準的な色彩的複圏 $`\mrm{Multi}(\cat{V})`$ を構成できます。この複圏を使うと、複圏の $`\cat{V}`$ への表現とは、次のような複関手（複圏のあいだの準同型射）のことになります。

$`\quad F: \cat{M} \to \mrm{Multi}(\cat{V}) \In {\bf MULTICAT}`$

ここで出てきた（小さいとは限らない）複圏達の集まり $`{\bf MULTICAT}`$ は2-圏となります。

0-射：小さいとは限らない複圏
1-射：複圏のあいだの複関手
2-射：複関手のあいだの自然変換

したがって、域・余域を固定した複関手の集まりは（自然変換を入れて）ホム圏になります。

$`\quad {\bf MULTICAT}(\cat{M}, \mrm{Multi}(\cat{V})) \;\in |{\bf CAT}|`$

ホム圏の対象は複圏の表現、射は表現のあいだの準同型射〈intertwiner〉（実体は複関手のあいだの自然変換）です。

こうして構成される複圏の表現達の圏を

$`\quad \mrm{MulticatRep}[\cat{M}](\cat{V}) \;\in |{\bf CAT}|`$

と書きます。対称モノイド圏 $`\cat{V}`$ としては、集合圏やベクトル空間の圏がよく使われます。表現の圏がホム圏で与えられる状況は、「Diag構成の変種とその書き方」の事例にもあります。

ローヴェア圏と単彩的複圏

ローヴェア圏〈ローヴェア・セオリー〉と単彩的複圏〈単色オペラッド〉のあいだの相互変換について概略を述べます。

ローヴェア圏 $`\cat{L} = (\cat{L}, e)`$ （記号の乱用）が与えられたとします。$`\cat{L}`$ の対象の集合を自然数と同一視して、$`|\cat{L}| = {\bf N}`$ だとします。$`\cat{L}`$ のモドイド構造は $`(\cat{L}, \otimes, I)`$ とします。$`\cat{L}`$ から単彩的複圏 $`\cat{M}`$ を作りましょう。使う構成法は、モノイド圏から複圏を作る一般的なものです。

$`\cat{M}`$ のオペセット〈複ホムセット〉は次のように定義します。

$`\For n \in {\bf N}\\
\quad \cat{M}(n ) := \cat{L}(n, 1) \;\in |{\bf Set}|
`$

先に複圏の恒等〈垂直単位〉を定義しておきます。

$`\Subject \mrm{i} \in \cat{M}(1)\\
\quad \mrm{i} := \id_1 \;\in \cat{L}(1, 1) = \cat{M}(1)
`$

次に複圏としての単純結合を定義します。

$`\For n, m \in {\bf N}\\
\For 1 \lt k \lt m\\
\Subject (;_k) : \cat{M}(n) \times \cat{M}(m) \to \cat{M}(n + m - 1) \In {\bf Set}\\
\For f \in \cat{M}(n) = \cat{L}(n, 1)\\
\For g \in \cat{M}(m) = \cat{L}(m, 1)\\
\quad f \,;_k g := (\mrm{i}^{\otimes(k - 1) }\otimes f \otimes \mrm{i}^{\otimes(m - k) }); g
\;\in \cat{L}(n + m - 1, 1) = \cat{M}(n + m - 1)
`$

こうして作った $`\cat{M}`$ が、単彩的複圏になることは（$`\cat{L}`$ が厳密モドイド圏なので）容易に示せます。

今度は逆に、単彩的複圏 $`\cat{M}`$ が与えられたとして、ローヴェア圏 $`\cat{L}`$ を構成します。ローヴェア圏はデカルト厳密モノイド小圏なので、$`\cat{L}(n, 1) = \cat{M}(n)`$ であるような最小のデカルト厳密モノイド小圏を自由生成します。

自由生成のひとつの方法として、$`\cat{M}`$ の複射と以下のようなデカルト・モノイド圏の基本射を“生成系”にします。

$`\cat{M}(n)`$ の要素 $`f`$ ： $`f: n \to 1`$
対称射〈スワップ〉： $`\mrm{X} : 2 \to 2`$
コピー射 $`\Delta: 1 \to 2`$
削除射 $`!: 1 \to 0`$

これらから結合と厳密モノイド積で“項”を作って、デカルト・モノイド圏の公理により商をとります。でき上がったデカルト・モノイド圏が $`\cat{L}`$ です。$`\cat{L}`$ の作り方から、対象集合 $`|\cat{L}|`$ は $`{\bf N}`$ で、モノイド積〈デカルト積〉は足し算になります。したがって $`\cat{L}`$ はローヴェア圏です。

おわりに

「全体像」に出した図式を以下に再掲します。

等式的代数指標を生成系として単彩的複圏を生成できます。逆向きに、単彩的複圏を等式的代数指標とみなす忘却関手があれば、自由忘却随伴系になるでしょう（たぶん）。

単彩的複圏を生成系としてローヴェア圏（デカルト・モノイド圏）を生成できます。ローヴェア圏の一部だけを抜き出して単彩的複圏を作れます。一部だけ抜き出して他を捨てているので、これは忘却関手とみなせます。単彩的複圏とローヴェア圏のあいだにも自由忘却随伴系があるでしょう。実際は随伴より強く、圏同値になっていそうです。

$`{\bf MonocMulticat}`$ と $`{\bf LawTh}`$ の圏同値に誘導されて、単彩的複圏の表現の圏とローヴェア圏のモデルの圏も圏同値のはずです。

文末が「でしょう」や「はずです」で歯切れが悪いのですが、細部の確認をさぼっているからです。このようなフレームワークでスケマティック系（「スケマティック系のために：雑多な予備知識 // 絵図的手法とスケマティック系」参照）が定義できたらいいなと思っています。