「カン拡張/カン持ち上げと上ホム対象/下ホム対象、充填三角形」への補遺です。
内容:
ペースティング図の充填問題
以下は「カン拡張/カン持ち上げと上ホム対象/下ホム対象、充填三角形」で出した右カン拡張に関わるペースティング図です。
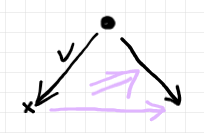
これを見てすぐ「なるほど確かに右カン拡張だ」と判断できる人もいるでしょうが、図の描き方(ペースティング図かストリング図か)や描画方向・レイアウトが変わると戸惑うこともあるでしょう。見た目が違う図を構造的に同じだと判断するのはけっこう難しい作業でトレーニングが必要です(以下の過去記事参照)。
図を見ての判断や理解は、ラベルの有り無しや、どんなラベルを付けるかにも影響されます。上記のラベル無しペースティング図に、ラベルを付けてみましょう。スパンの軸脚(「カン拡張/カン持ち上げと上ホム対象/下ホム対象、充填三角形」参照)を $`K`$ 、もう一方の脚を $`F`$ として、頂点にも名前を付けます。
$`\newcommand{\cat}[1]{\mathcal{#1}}
\quad \xymatrix{
{}
&\cat{C} \ar[dl]_{K} \ar[dr]^{F}
&{}
\\
\cat{D}\ar[rr]_{?1} \ar@{}@/^/[rr]^{\Rightarrow\, ?2}
&{ }
&\cat{E}
}\\
\quad \text{ in }{\bf CAT}
`$
カン拡張の話なので、ペースティング図は、大きい〈小さいとは限らない〉圏達の圏 $`{\bf CAT}`$ 内に描かれます。名前が付けられた頂点と辺 $`\cat{C}, \cat{D}, \cat{E}, K, F`$ は既知〈known〉あるいは所与〈given〉です。疑問符でラベルされている1-射〈関手〉と2-射〈自然変換〉が未知〈unknown〉です。
この図式を、疑問符部分を埋める一種の方程式と考えて、その解が(“カン”とは限らない)右拡張です。右拡張は、(ペースティング図で見れば)閉じてないニ辺形であるスパンを充填する三角形です。ニ辺形の三角形による充填問題の解が右拡張と言えます。あまた在るかも知れない右拡張のなかで、最も良い右拡張が右カン拡張です。
最も良い解が $`(G, \rho)`$ だとして、ペースティング図に最も良い解のラベルを書き込むと次のようです。
$`\quad \xymatrix{
{}
&\cat{C} \ar[dl]_{K} \ar[dr]^{F}
&{}
\\
\cat{D}\ar[rr]_{G} \ar@{}@/^/[rr]^{\Rightarrow\, \rho}
&{ }
&\cat{E}
}\\
\quad \text{ in }{\bf CAT}
`$
この $`(G, \rho)`$ を「何と呼び、どう書き記すか」は色々あるよ、ということを「カン拡張/カン持ち上げと上ホム対象/下ホム対象、充填三角形」に書いています。
ストリング図で描くと
同じ内容を、ペースティング図で描くか/ストリング図で描くかで、だいぶ印象が変わります。以下は「カン拡張/カン持ち上げと上ホム対象/下ホム対象、充填三角形」の図の再掲ですが、欄に入っている絵はペースティング図です。
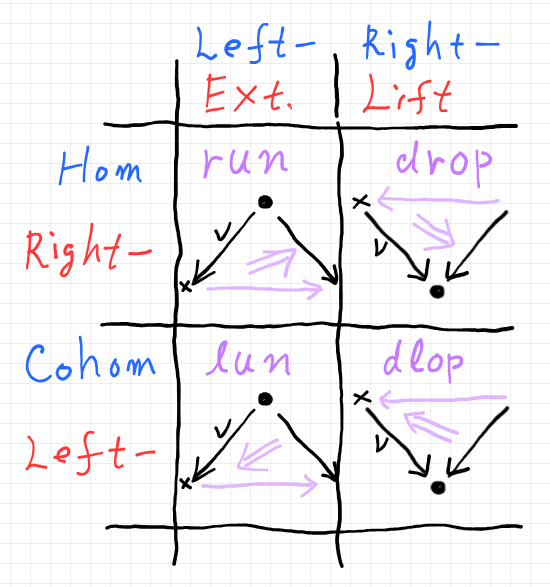
同じ内容を、ストリング図(レンガ色)とペースティング図を重ねて描くと次のようです。
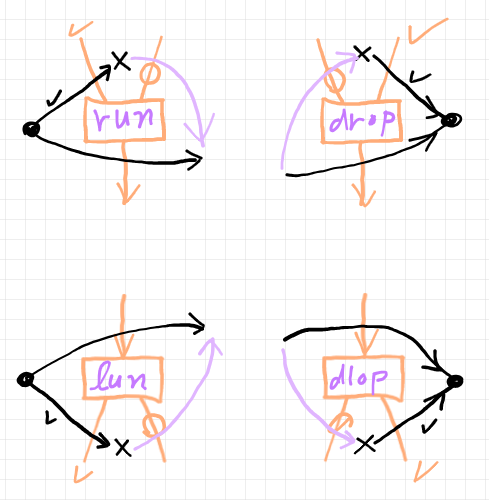
ストリング図の描画方向は、左から右に関手の結合方向、上から下に自然変換の縦結合方向です。ストリング図の描画方向に合わせるために、ペースティング図に鏡映や回転の変換を施しています(「双対や随伴に強くなるためのトレーニング」参照)。
スパン/コスパンを三角形で充填する問題の解である2次元の射が、ストリング図ではボックスで描かれています。ボックスのラベルである run, lun, drop, dlop がそれぞれ、右カン拡張、左カン拡張、右カン持ち上げ、左カン持ち上げを構成する2-射〈自然変換〉のラベル〈構成素名〉です。