圏論的レンズ 2：具象オプティック - 檜山正幸のキマイラ飼育記 (はてなBlog)

$\newcommand{\Iff}{\Leftrightarrow } \newcommand{\id}{\mathrm{id} } \newcommand{\In}{\text{ in } } \require{color} \newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }% \newcommand{\For}{\Keyword{For } }% \newcommand{\Define}{\Keyword{Define } }% \newcommand{\Where}{\Keyword{Where } }% \newcommand{\When}{\Keyword{When } }% \newcommand{\Holds}{\Keyword{Holds } }% \newcommand{\Declare}{\Keyword{Declare } }%$ 「圏論的レンズ最初の一歩：ストリング図を中心に」において、元祖レンズと具象レンズを紹介しました。元祖レンズを少し一般化すると具象レンズになるのでした。この記事では、具象レンズをさらに少し一般化して具象オプティックを導入します。

[追記]この記事で導入した具象オプティックは具象レンズの一般化ではなくて、具象レンズ＝具象オプティックでした。詳しくは「圏論的レンズ訂正と補足：具象レンズ＝具象オプティック」を参照してください。[/追記]

内容：

具象オプティックとは
具象オプティックの実装と外部ビュー
具象オプティック実装の描き方
順行／逆行パートのボディとコーデック
具象オプティック実装あいだののスライディング同値関係
具象オプティックの圏の結合と恒等

最初の記事＋シリーズ目次

具象オプティックとは

具象レンズが「具象〈concrete〉」と呼ばれるのは、集合圏をベースにしているからです。抽象的・一般的な圏をベースにしてはいません。同じように、集合圏をベースに*1定義したオプティックを具象オプティック〈concrete optic〉と呼ぶことにします。とは言っても「オプティックってなんだ？」ってことになります。この節でおおよその説明をしましょう。

具象レンズ $f = (f_\#, f^\#) :(A, X) \to (B, Y) \In {\bf ConcLens}$ は、順行パート〈forward part〉と逆行パート〈backward part〉から構成されます。

順行パート： $f_\# : A \to B \In {\bf Set}$
逆行パート： $f^\# : A \times Y \to X \In {\bf Set}$

順行パートと逆行パートが対称的ではないですね。順行パート／逆行パートのプロファイル（域と余域）を次のように変更すると対称的になります。

順行パート： $f_\# : A \to R\times B \In {\bf Set}$
逆行パート： $f^\# : R \times Y \to X \In {\bf Set}$

ここで出てきた集合 $R$ を残余〈residual〉と呼びます*2。

適当な残余を伴った対称的なプロファイルを持つ順行・逆行ペア $(f_\#, f^\#)$ がおおよそ具象オプティックです。「おおよそ」と言ったのは、具象オプティックをちゃんと定義するには同値関係による商集合を作るからです。商集合の構成はこの記事全体のテーマです。

具象レンズの場合と同様に、具象オプティックの全体も圏 ${\bf ConcOptic}$ を形成します。実際には、圏 ${\bf ConcOptic}$ をちゃんと定義した後で「この圏の射が具象オプティックだ」と言うべきですが。

[追記]次の段落は、僕の誤った印象に基づいて書かれています。印象とは、ハッキリと確認してないボンヤリした認識のことです。文言はそのまま残しますが、別な記事で訂正と補足をします。[/追記][さらに追記]「圏論的レンズ訂正と補足：具象レンズ＝具象オプティック」を書きました。[/さらに追記]

具象オプティックを定義すると、具象レンズは特殊な具象オプティックとみなせます。「圏論的レンズ最初の一歩：ストリング図を中心に」において、具象レンズの圏 ${\bf ConcLens}$ の形式的定義は省略しましたが、具象オプティックの圏 ${\bf ConcOptic}$ をちゃんと定義すれば、具象レンズの圏はその部分圏として確定します； ${\bf ConcLens} \subseteq {\bf ConcOptic}$ 。

[追記] ${\bf ConcLens} = {\bf ConcOptic}$ となります。[/追記]

具象オプティックの実装と外部ビュー

具象オプティックの集合（ホムセット）は商集合として構成します。なので、次の段落で商集合に関して短く要約します。

集合 $X$ 上に同値関係〈equivalence relation〉 $\sim$ があって、 $Q := X/\sim$ を同値関係による商集合〈quotient set〉とします。規準的〈canonical〉な射影〈projection〉 $\pi: X \to Q$ が決まります。 $[x] := \pi(x)$ という書き方がよく用いられます。 $q\in Q$ に対して $[x] = q$ のとき、 $x$ は“同値類〈equivalence class〉 $q$ の代表元〈representative〉”といいます。

具象オプティックに関しては、上記の標準的な用語法以外にソフトウェア的比喩に基づく言葉も使います*3。

とある集合 $X$ の要素を、具象オプティックの実装〈implementation〉と呼ぶ。（とある集合については後述）
とある同値関係 $\sim$ による商集合 $Q := X/\sim$ の要素、つまり同値類を、具象オプティックの外部ビュー〈external view〉と呼ぶ。（とある同値関係については後述）

具象オプティックを双方向データ変換ソフトウェアと捉えるときは、このような言葉づかいがシックリ来ると思います（後述）。この記事では、他にもソフトウェア的言葉を適宜使います。

さて、具象オプティックの圏 ${\bf ConcOptic}$ を定義していきましょう。まずは対象類から。

対象類： $|{\bf ConcOptic}| := |{\bf Set}|\times |{\bf Set}|$

${\bf ConcOptic}$ の対象は集合のペア $(A, X)$ です。

次は、2つの対象 $(A, X), (B, Y)$ に対して、ホムセットを定義したいですよね。が、これはちょっと面倒で、ホムセットになる手前の集合を先に準備する必要があります。

集合 $R$ に対して次のように定義します。

$\For R \in |{\bf Set}|\\ \Define {\bf ConcOpticImpl}_R ( (A, X), (B, Y)) := \\ \quad \{ (f_\#, f^\#) \mid f_\# : A \to R\times B,\, f^\# : R \times Y \to X \In {\bf Set} \}$

これは、前節で述べた“残余を $R$ とするおおよそ具象オプティック”の集合になります。“おおよそ具象オプティック”という代わりに“具象オプティック実装”と呼び替えます。つまり、今定義した集合は、

プロファイルが $(A, X) \to (B, Y)$ であり、 $R$ を残余とする具象オプティック実装〈concrete optic implementation〉の集合

です。

次のように定義しても同じです。

$\For R \in |{\bf Set}|\\ \Define {\bf ConcOpticImpl}_R ( (A, X), (B, Y)) := \\ \quad {\bf Set}(A, R\times B)\times {\bf Set}(R\times Y, X)$

ここまで、残余 $R$ を固定してましたが、様々な残余をすべて考えた具象オプティック実装全体の集合は次のようになります。

$\Define {\bf ConcOpticImpl} ( (A, X), (B, Y)) := \\ \quad {\displaystyle \bigcup_{R\in |{\bf Set}|} {\bf ConcOpticImpl}_R ( (A, X), (B, Y)) }$

「集合」と言いましたが、今定義した ${\bf ConcOpticImpl} ( (A, X), (B, Y))$ は集合論で認められた集合ではありません。大きな集合〈large set〉（真の類〈proper class〉）です。オプティックの説明では、集合のサイズ（大きな集合かどうか）に無頓着で、杜撰な扱いがされています。「よくないなー」と思いますが、ここで詮索するのはやめておきます。

プロファイルを固定しても、ありとあらゆる残余を考えた具象オプティック実装の集まりは、集合とは呼べないほどの巨大な集まり〈大きな集合 | 真の類〉になることは気に留めておいてください。ただし、楽観的習慣に従い、大きな集合も単に「集合」と呼んでしまいます。

集合（大きいけどね） ${\bf ConcOpticImpl} ( (A, X), (B, Y))$ に適切な同値関係を入れて作った商集合が、我々が目的とするホムセット ${\bf ConcOptic} ( (A, X), (B, Y))$ です。“商集合の要素＝同値類”を具象オプティックの外部ビューとも呼ぶと約束しました。単に具象オプティック〈concrete optic〉と言った場合は外部ビューを指します。

具象オプティック＝具象オプティック外部ビュー＝具象オプティック実装からなる同値類

外部ビューという呼び名にしたのは、実装に依存する内部構造（の一部）が隠蔽されて見えなくなったモノだからです（後で再度触れます）。今後の話で「外部ビュー ←→ 内部構造」の対比を意識してください。

適切な同値関係による商集合としてのホムセットの構成の手順は次節以降で述べます。

具象オプティック実装の描き方

圏 ${\bf ConcOptic}$ のホムセットの構成を説明するには、ストリング図を使うのが最もわかりやすいでしょう。「圏論的レンズ最初の一歩：ストリング図を中心に」と同様に、次の描画法を使います。

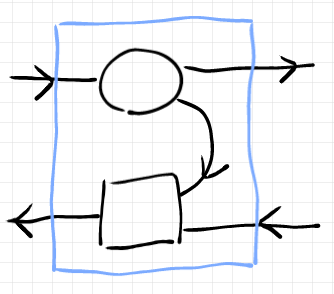
上の図は具象オプティック実装のストリング図です。上段の左から右が順行方向、下段の右から左が逆行方向です。順行方向に対する直積の方向は下から上、逆行方向に対する直積の方向は上から下です。行きがかり上、順行パートは丸で、逆行パートは四角で表しました。残余は曲がったワイヤーで表します。全体を囲む水色の枠は、単なる包装箱〈packing box〉で、なにかの機能を表すものではありません。

レンズやオプティックの議論においてストリング図の使用は本質的です。以下の記事でストリング図の描き方は確認しておいてください。

ストリング図計算のコツと小技

具象オプティック実装（や一般化されたオプティックの実装）の描画法は人により場合により様々です。順行パートを左に、逆行パートを右に配置して、凹形の包装箱で囲んでみると次のようになります。

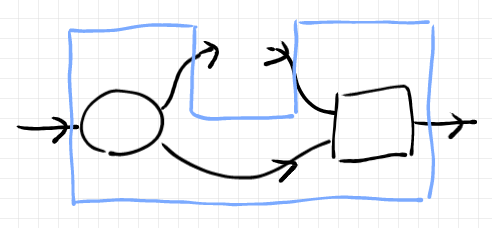
ロマン（Mario Roman）やライリー（Mitchell Riley）は、凹形の上下を逆にして描く方法を採用しています -- そういう描画法だと、結合〈composition〉の際にサイズの縮小・拡大をしなくてはならないので僕は嫌いです。

具象オプティック実装の順行パート／逆行パートとして、単一のノードでなくストリング図が入ると、どれが残余のワイヤーか迷うことがあります。ハッキリわかるように、残余ワイヤーには短い横線を入れることにします。以下のようです（赤でマークした所が短い横線）。

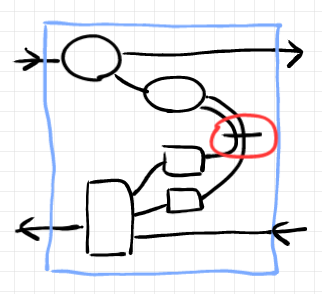
水色の包装箱は特に必要がなければ省略することが多いです。

レンズ／オプティックの議論では、図を縦にしたり横にしたり、ひっくり返したり変形したりを頻繁に行います。これらの操作に達者になるには「双対や随伴に強くなるためのトレーニング」をしましょう*4。

順行／逆行パートのボディとコーデック

具象オプティック実装のソフトウェア的解釈（のひとつ）は双方向データ変換ソフトウェアです。そう解釈したとき、残余は内部通信用のデータ型になります。

具象オプティック実装 $f = (f_\#, f^\#)$ の順行パート $f_\#$ のプロファイルは、

$\quad f_\#: A \to R \times B \In {\bf Set}$

なので、外部（箱の外）への出力型 $B$ とは別に内部向け出力型 $R$ を持ちます。それが残余です。

順行パートから出力された型 $R$ の内部データは、逆行パートによって利用されます（別に利用しないで捨ててもいいけど）。だから、逆行パートのプロファイルは次の形なのです。

$\quad f^\#: R \times Y \to X \In {\bf Set}$

前節で取り決めた描画法において、残余の曲がったワイヤーは、具象オプティック実装の内部でだけ使われるプライベートチャンネル（外部には公開されない通信路）を表します。内部のプライベート通信がちゃんと行われるためには、内部通信用のデータ型 $R$ を決めておく必要があります。

今、目の前にある関数 $g$ のプロファイルが $g:A \to S\times B$ だったとします。 $S \ne R$ のとき、 $f$ の順行パート $f_\#$ を $g$ で置き換えることはできません。内部通信のプロトコル（約束事）を守ってないからです。

しかし、 $e:S \to R$ という関数を準備して $g;(e \times \id_B)$ を作ると、 $f_\#$ を置き換えることができます。 $e$ は、違法なデータ型 $S$ から正式なデータ型 $R$ へのエンコーダー〈encoder〉だと考えましょう。もとの関数 $g$ は処理の本体だと考えてボディ〈body〉と呼びます。

ボディ $g$ とエンコーダー $e$ から具象オプティック実装の順行パート $g;(\id_B \times e)$ を組み立てること、あるいは逆に、既存の順行パートをボディとエンコーダーに分解することは、しばしば行われる重要な操作です。

同様に、ボディ $h:T\times Y \to X$ とデコーダー〈decoder〉 $d:R \to T$ から具象オプティック実装の逆行パート $(d \times \id_Y); h$ を組み立てること、あるいは逆に、既存の逆行パートをボディとデコーダーに分解することも重要です。

順行／逆行パートのボディとコーデック（エンコーダーとデコーダー）のプロファイルをまとめると次のようです。ストリング図を描いて確認しましょう。

順行パートのボディ： $g: A \to S \times B \In {\bf Set}$
順行パートのエンコーダー： $e: S \to R \In {\bf Set}$
順行パート： $g;(e \times \id_B) : A \to R \times B \In {\bf Set}$
逆行パートのボディ： $h: T \times Y \to X \In {\bf Set}$
逆行パートのデコーダー： $d: R \to T \In {\bf Set}$
逆行パート： $(d \times \id_Y); h : R\times Y \to X \In {\bf Set}$

具象オプティック実装あいだののスライディング同値関係

いよいよ、（大きな）集合 ${\bf ConcOpticImpl} ( (A, X), (B, Y))$ 上の同値関係を定義しましょう。関係 $\approx$ （同値関係のもとになるが、同値関係ではない）を次のように定義します。

$\For f = (f_\#, f^\#) \in {\bf ConcOpticImpl}_R ( (A, X), (B, Y))\\ \For g = (g_\#, g^\#) \in {\bf ConcOpticImpl}_S ( (A, X), (B, Y))\\ \Define f \approx g :\Iff\\ \quad \exists u:S \to R \In {\bf Set}.\, f_\# = g_\# ;(u \times \id_B) \,\land\, g^\# = (u \times \id_Y); f^\#$

テキストの論理式で書かれると、なんのことやら分かりませんが、ストリング図で描けば意味は明白です。次のルールで描画します。

順行パートを構成するノードは丸
逆行パートを構成するノードは四角
$f$ を構成するノードは斜線網掛け
$g$ を構成するノードは砂目網掛け
コーデック（エンコーダー／デコーダー） $u$ はベタ塗り

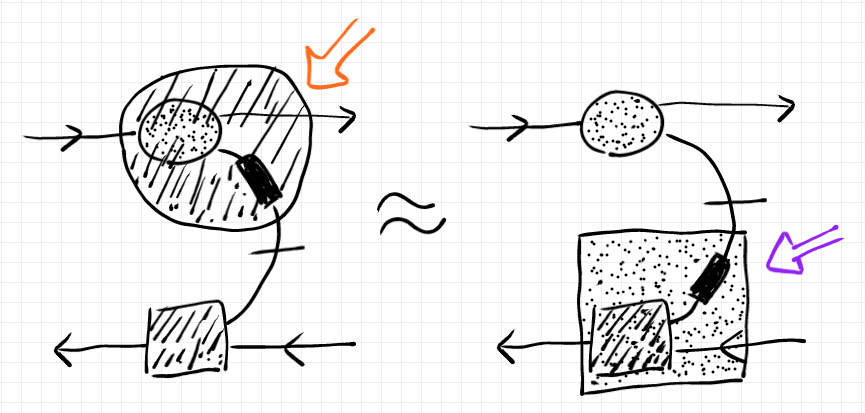
オレンジ色の矢印が指している場所に注目すると、次の等式がわかります。

$\quad f_\# = g_\# ;(u \times \id_B)$

紫色の矢印が指している場所に注目すると、次の等式がわかります。

$\quad g^\# = (u \times \id_Y); f^\#$

斜線や砂目が鬱陶しいので、もっとスッキリ描けば次のようです。

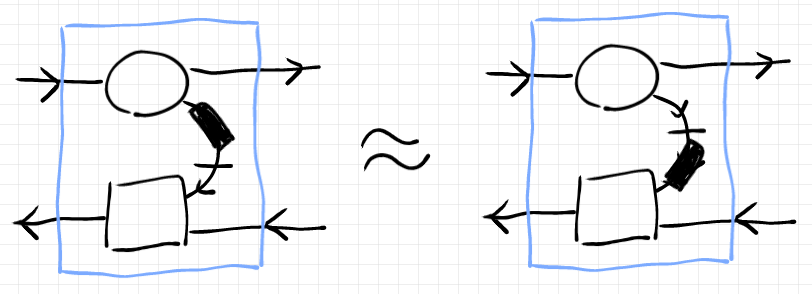
要するに、ベタ塗りのコーデック $u$ は曲がったワイヤーに沿ってスライドさせてもいいよ、ってことです。

今定義した関係 $\approx$ をストリング図の変形操作と考えると、次の手順を実行することになります。

具象オプティック実装 $f$ の順行パート $f_\#$ をボディとエンコーダーに分解する。
エンコーダー $u$ を、残余のワイヤーに沿って逆行パート側まで移動する。
$u$ は、逆行パート側でデコーダーになる。

逆向きの操作なら：

具象オプティック実装 $g$ の逆行パート $g^\#$ をボディとデコーダーに分解する。
デコーダー $u$ を、残余のワイヤーに沿って順行パート側まで移動する。
$u$ は、順行パート側でエンコーダーになる。

関係 $\approx$ は反射律は満たしますが、同値関係ではありません。上で述べたような操作（逆向きのストリング図変形も許す）を何回か繰り返して移りあえる2つの具象オプティック実装 $f,\, g$ は $f \sim g$ だと定義すれば、関係 $\sim$ は対称律・推移律も満たし同値関係になります。

念の為に、関係 $\approx$ と関係 $\sim$ の“関係”を述べておくと：

$f \approx g$ ならば、 $f \sim g$ である。
$g \approx f$ ならば、 $f \sim g$ である。
$f \sim h$ かつ $h \sim g$ ならば、 $f \sim g$ である。
上記の場合以外で $f \sim g$ となることはない。

同値関係 $\sim$ は、圏論の用語ではコエンド同値〈coend equivalence〉と呼ばれますが、ここでは、ストリング図の印象からスライディング同値〈sliding equivalence〉と呼ぶことにします。

スライディング同値 $\sim$ は集合 ${\bf ConcOpticImpl} ( (A, X), (B, Y))$ 上の同値関係なので商集合を作れます。その商集合が圏 ${\bf ConcOptic}$ のホムセットです。

$\For (A, X), (B, Y) \in |{\bf ConcOptic}| \\ \Define {\bf ConcOptic}( (A, X), (B, Y)) := \\ \quad ({\bf ConcOpticImpl} ( (A, X), (B, Y)))/\sim$

商集合 ${\bf ConcOptic}( (A, X), (B, Y))$ の要素が具象オプティック〈concrete optic〉です。具象オプティックは同値類なので、代表元として具象オプティック実装を持ちます。それを具象オプティックの代表実装〈representative implementation〉と呼ぶことにします。

具象オプティック実装 $f = (f_\#,f^\#)$ が代表する具象オプティックを $\langle f_\# \mid f^\#\rangle$ と書く習慣です。つまり：

$\quad \langle f_\# \mid f^\#\rangle := [(f_\#,f^\#)] = \pi( (f_\#,f^\#))$

同値関係と同値類代表元の一般論から次が言えます。

$\quad ( f_\# , f^\#) \sim ( g_\# , g^\#) \Iff \langle f_\# \mid f^\#\rangle = \langle g_\# \mid g^\#\rangle$

具象オプティック実装においては、内部構造が違えばそれは違う実装です。しかし、同値類である具象オプティックでは、多少の内部構造の違いがあっても“同じ”とみなします。残余の選び方やコーデックをどこに配置するかは、外からソフトウェアを見る立場からはどうでもいいことだし、隠蔽されるべき情報です。つまり、同値類である具象オプティックは外部ビュー〈external view〉を提供することになります。

具象オプティックの圏の結合と恒等

具象オプティックは具象オプティック実装の同値類として定義されました。これは、有理数が分数の同値類として定義されているのと事情は同じです。

具象オプティック：具象オプティック実装＝有理数：分数

有理数の計算を分数による表示を通して行うのと同様に、具象オプティックの計算は適当な代表実装を取って行います。具象オプティックの結合も、代表実装に対して演算を定義して、その演算が代表実装の取り方によらないこと（well-defined条件）を示します。

結合演算の定義のために、残余に関する準備が必要です。具象オプティック実装の順行パート／逆行パートには、残余 $R$ が次の形で出現します。

$f_\#: A \to R\times B \In {\bf Set}$
$f^\#: R\times Y \to X \In {\bf Set}$

余域側に出現する残余を残余出力〈residual output〉、域側に出現する残余を残余入力〈residual input〉と呼ぶことにします*5。

残余出力を持つ関数（具象オプティック実装の順行パートでなくてもよい） $f:A \to R\times B$ の全体を ${\bf Set}(A, B)_{R\times}$ と書くことにします。つまり：

$\quad f \in {\bf Set}(A, B)_{R\times}\\ \Iff f \in {\bf Set}(A, R\times B)\\ \Iff f:A \to R\times B \In {\bf Set}$

同様に、残余入力を持つ関数 $g:R\times A \to B$ の全体を ${\bf Set}_{R\times}(A, B)$ と書くことにします。

$\quad g \in {\bf Set}_{ R\times}(A, B)\\ \Iff g \in {\bf Set}(R\times A, B)\\ \Iff f:R\times A \to B \In {\bf Set}$

残余出力を持つ関数どうしの特別な結合 $;_\bullet$ を次のように定義します。

$\For f \in {\bf Set}(A, B)_{R\times}\\ \For g \in {\bf Set}(B, C)_{S\times}\\ \Declare f;_\bullet g \in {\bf Set}(A, C)_{(R\times S)\times}\\ \Define f;_\bullet g := f;(\id_R \times g );\alpha_{R, S, C}^{-1}$

ここで、 $\alpha_{R, S, C}$ は直積の結合律子〈associator〉です。

$\quad \alpha_{R, S, C}: (R\times S) \times C \to R\times (S \times C )\\ \quad \alpha_{R, S, C}^{-1}: R\times(S \times C) \to (R\times S) \times C$

同様に、残余入力とを持つ関数どうしの特別な結合 ${_\bullet};$ を次のように定義します。

$\For f \in {\bf Set}_{R\times}(A, B)\\ \For g \in {\bf Set}_{S\times}(B, C)\\ \Declare f {_\bullet}; g \in {\bf Set}_{(S\times R)\times}(A, C)\\ \Define f {_\bullet}; g := \alpha_{S, R, A}; (\id_S \times f);g$

これらの特別な結合が何を意味するかはストリング図を描いてみれば明らかだと思います。

さて、準備が出来たので具象オプティックの結合を定義します。

$\For f = \langle f_\#, f^\# \rangle : (A, X) \to (B, Y) \In {\bf ConcOptic}\\ \Where \\ \quad f_\# : A \to R\times B \In {\bf Set}\\ \quad f^\# : R\times Y \to X \In {\bf Set}\\ \For g = \langle g_\#, g^\# \rangle : (B, Y) \to (C, Z) \In {\bf ConcOptic}\\ \Where \\ \quad g_\# : B \to S\times C \In {\bf Set}\\ \quad g^\# : S\times Z \to Y \In {\bf Set}\\ \Define f;;g := \langle f_\# ;_\bullet g_\# \mid g^\# {_\bullet}; f^\# \rangle\\ \Where \\ \quad f_\# ;_\bullet g_\# : A \to (R\times S)\times C \In {\bf Set}\\ \quad g^\# {_\bullet}; f^\# : (R\times S)\times Z \to X \In {\bf Set}$

この結合をストリング図で描くと次のようになります。手違いで前の図とは塗りパターンが異なってしまい、 $f$ が砂目網掛けで $g$ が斜線網掛けです。結合記号のコロン2個は縦に並べています。

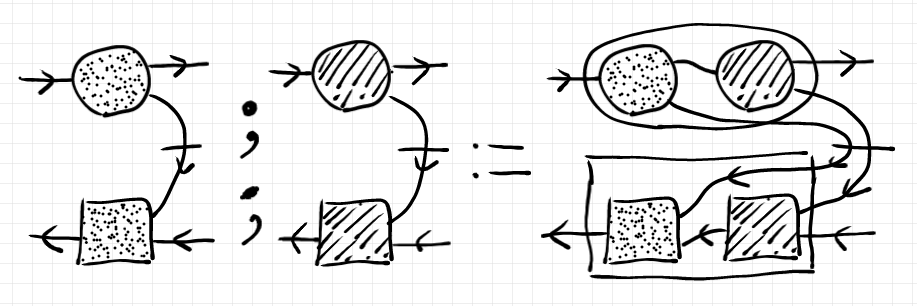
以上のように定義しただけではwell-defined性が確認されてません。次の命題（定義の正当性条件）を示す必要があります。

$\When (f_\#,f^\#) \sim (f'_\#,f'^\#) \,\land\, (g_\#,g^\#) \sim (g'_\#,g'^\#) \\ \Holds (f_\# ;_\bullet g_\# , g^\# {_\bullet}; f^\#) \sim (f'_\# ;_\bullet g'_\# , g'^\# {_\bullet}; f'^\#)$

この命題は練習問題とします。

恒等具象オプティック $\mathrm{oid}$ （optic id）は次のように定義します。

$\For (A, X)\in |{\bf ConcOptic}|\\ \Define \mathrm{oid}_{(A, X)} := \langle \lambda_A^{-1} \mid \lambda_X \rangle$

ここで、 $\lambda$ は直積の左単位律子〈left unitor〉です。

$\quad \lambda_X : {\bf 1}\times X \to X \In {\bf Set}\\ \quad \lambda_A^{-1} : A \to {\bf 1}\times A \In {\bf Set}$

結合演算と恒等射が定義されても、圏の法則を満たさなければ圏とは呼べません。次の法則達を確認する必要があります。

$\For f:(A, X) \to (B, Y) \In {\bf ConcOptic}\\ \For g:(B, Y) \to (C, Z) \In {\bf ConcOptic}\\ \For h:(C, Z) \to (D, W) \In {\bf ConcOptic}\\ \Holds (f;;g);;h = f;;(g ;; h)\\ \:\\ \For f:(A, X) \to (B, Y) \In {\bf ConcOptic}\\ \Holds \mathrm{oid}_{(A, X)};;f = f\\ \Holds f;;\mathrm{oid}_{(B, Y)} = f$