環境付き計算と依存アクテゴリー 1/n - 檜山正幸のキマイラ飼育記 (はてなBlog)

カプチ／マイヤース〈Matteo Capucci, David Jaz Myers〉の依存アクテゴリーは、アクテゴリーと二重圏の中間にある、ほど良い感じの概念的フレームワークです（「依存アクテゴリーが面白い」参照）。まだ定義さえハッキリしない状態ですが、僕は期待してます。

「依存アクテゴリーに向けて」より：

事例がないと何していいか分からないので、事例を探すことにします。

けっこう良い例が見つかった！別に新しいモノではなくて、昔から僕が使っていた構造です。が、依存アクテゴリーだと思って眺めると、新しい側面が見えて新鮮です。$`\newcommand{\mrm}[1]{ \mathrm{#1} }
\newcommand{\cat}[1]{ \mathcal{#1} }
\newcommand{\In}{\text{ in }}
%\newcommand{\u}[1]{\underline{#1}}
%\newcommand{\twoto}{ \Rightarrow }
\newcommand{\id}{ \mathrm{id} }
\newcommand{\hyp}{\text{－} }
\newcommand{\dimU}[2]{ {{#1}\!\updownarrow^{#2}} }
\newcommand{\NFProd}[3]{ \mathop{_{#1} \!\underset{#2}{\times}\,\!_{#3} } }
%\newcommand{\dblcat}[1]{\mathbb{#1}}
`$

内容：

環境付き計算（懐旧）
環境付き計算のインデックス付き圏
グロタンディーク構成とファイブレーション
依存アクテゴリー
モノイド法則
環境付き計算ペアのミックス操作
ベース射の自明持ち上げ
自明持ち上げの法則
2-圏内のスパンのあいだの射

関連記事：

環境付き計算（懐旧）

入力の型 $`A`$ と出力の型 $`B`$ 以外に、状態の型 $`S`$ を持った計算は、次の写像で表現できます。

$`\quad f: S \times A \to S \times B \In {\bf Set}`$

$`f`$ は状態（$`S`$ の要素）と入力（$`A`$ の要素）を受け取って、状態と出力（$`B`$ の要素）を返します。つまり、$`f`$ は状態を更新できます。

もし、状態が読み取り専用〈リードオンリー | イミュータブル〉ならば、$`f`$ は状態を読み取って使えますが、状態更新はできません。そのとき、$`f`$ のプロファイル（入出力の仕様）は次のようになります。

$`\quad f: S \times A \to B \In {\bf Set}`$

読み取り専用の状態を環境〈environment〉とも言います。参照だけできる環境を持つ計算、あるいはそんな計算を表現する写像を環境付き計算〈computation with environment〉と呼びます。

環境付き計算は随分と昔から話題にしてますね。

双対性と環境付き計算 (2011年)
try-catchの双対となる構造 (2011年)

環境付き計算は、集合圏に限らず一般にデカルト圏で定義できます。デカルト圏ではデカルト積による掛け算〈スタンピング | テンソリング〉があります。デカルト圏の任意の対象 $`S`$ はコモノイド構造を持つので、$`S`$ の掛け算はコモノイドのスタンピングとなり、コモノイド・コスタンピング・コモナド*1を定義します。このコモナドの余クライスリ圏の射が環境 $`S`$ を持つ環境付き計算を表現します。

“$`S`$-環境付き計算の圏”の $`S`$ を動かすと、インデックス付き圏が定義できます。このインデックス付き圏からグロタンディーク構成を行うと、環境を固定しない（すべての環境を考慮する）環境付き計算達の圏が作れます。このことも古い記事で（アウトラインだけ）述べています。

デカルト圏の掛け算から作るインデックス付き圏の例 (2011年)

比較的最近だと、以下の過去記事の「環境・前提付き計算」と「コモノイド・コスタンピング構成」の節で同じ内容を（別な文脈と手法で）述べています。

最近の型理論：型判断／シーケントの意味論に向けて (2023年)

上記2023年の過去記事で「環境・前提」という言葉を使っているのは、環境（読み取り専用状態）という概念をカリー／ハワード／ランベック対応で論理に移すと、証明で使ってよい背景的前提（明示的な仮定とは別）になるからです。

以上は昔〈過去〉の話でしたが、次節以降であらためて環境付き計算を説明します。

環境付き計算のインデックス付き圏

環境 $`S`$ ごとに、$`S`$-環境付き計算の圏が構成できて、$`S`$ を動かすとインデックス付き圏になります。そのことをこの節で説明します。

$`\cat{C} = (\cat{C}, \times, \mrm{I})`$ は、モノイド圏として定義されたデカルト圏〈デカルト・モノイド圏〉とします。デカルト圏の典型的な例は集合圏 $`({\bf Set}, \times, {\bf 1})`$ です。

$`S \in |\cat{C}|`$ に対して、新しい圏 $`\cat{C}_{(S\times)}`$ を次のように定義します*2。

対象： $`|\cat{C}_{(S\times)}| := |\cat{C}|`$ （対象の集合は同じ）
ホムセット： $`\text{For }A, B\in |\cat{C}_{(S\times)}| = |\cat{C}|`$
$`\quad \cat{C}_{(S\times)}(A, B) := \cat{C}(S\times A, B)`$ （$`S`$-環境付き計算）

射の結合と恒等射は次のストリング図のように定義します。

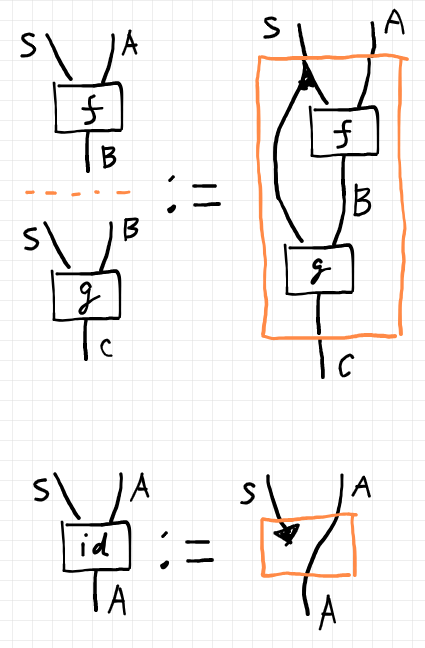
射の向きは上から下。
箱の上側左のワイヤーが環境、右のワイヤーが入力、下のワイヤーが出力。
オレンジ色の横向き破線は結合を表す。
オレンジの色の枠は、構成された射を表す。
黒い二股分岐は対角射〈コピー射〉、黒い小さな下向き三角形は終射〈削除射 | 破棄射〉。

こうして定義された射の結合と恒等射が、結合法則と左右の単位法則を満たすことは以下の絵等式（ストリング図のあいだの等式）から分かります。オレンジ色の枠はテキスト数式の括弧に相当するグルーピングです。大きなイコールの下にある等式は、大きなイコールが成立する根拠となる等式で、デカルト圏が備えるコモノイドの余結合法則と左右の余単位法則です。

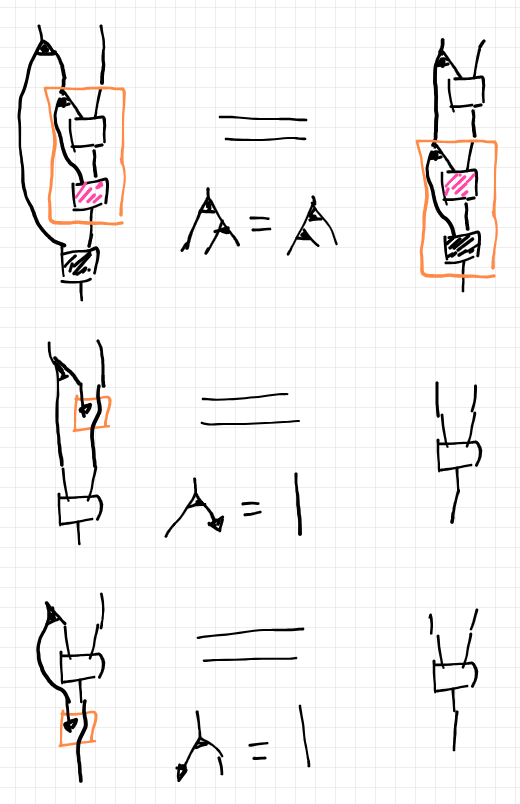
以上の定義と法則の確認により、以下の対応が作れました。

$`\quad |\cat{C}| \ni S \mapsto \cat{C}_{(S\times)} \in |{\bf CAT}|`$

次に、射 $`v:S \to T \In \cat{C}`$ に対して、次のような関手（圏達の圏の射）を構成しましょう。

$`\quad \cat{C}_{(v \times)} : \cat{C}_{(T\times)} \to \cat{C}_{(S\times)} \In \dimU{\bf CAT}{1}`$

$`\dimU{\bf CAT}{1}`$ は、圏達の2-圏から2-射〈自然変換〉を捨てた1-圏です。$`\dimU{\hyp}{1}`$ という書き方については、「圏の次元調整」を参照してください。

$`\cat{C}_{(T\times)}`$ の射 $`h: A\to B`$ を $`h: (T\times) A \to B`$ とも書くことにして、$`\cat{C}_{(\hyp \times)}`$ の定義は以下のようです。

対象パート： $`\text{For }A\in |\cat{C}_{(T\times)}|`$
$`\quad \cat{C}_{(v \times)}(A) := A`$ （対象に対しては恒等〈identity on objects〉）
射パート： $`\text{For }h : (T\times) A \to B \In \cat{C}_{(T\times)}`$
$`\quad \cat{C}_{(v \times)}(h: (T\times) A \to B) := (\, (v\times \id_A); h : (S\times) A \to B \,)`$

$`h: (T\times) A \to B`$ の $`(T\times)`$ は単なる注釈で、$`h`$ のプロファイルは $`A\to B \In \cat{C}_{(T\times)}`$ であることに注意してください。

上記の射パートを絵に描けば：

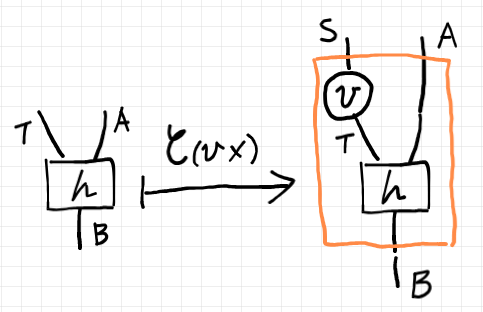
対象と射に対する対応 $`\cat{C}_{(\hyp \times)}`$ は次を満たします。ここでは、関手の結合をセミコロン '$`;`$' *3、恒等関手を '$`\mrm{Id}`$' で書いています。

$`\text{For }v: S \to T, w : T \to U \In \cat{C}\\
\quad \cat{C}_{(v; w \,\times)} = \cat{C}_{(v \times)} ; \cat{C}_{(w \times)}
: \cat{C}_{(C \times)} \to \cat{C}_{(A \times)}
\In \dimU{\bf CAT}{1} \\
\text{For } S \in |\cat{C}|\\
\quad \cat{C}_{( \id_S \times)} = \mrm{Id}_{\cat{C}_{(S \times)}} :
\cat{C}_{(S \times)} \to \cat{C}_{(S \times)} \In \dimU{\bf CAT}{1}
`$

射の結合 $`v;w`$ が $`\cat{C}_{(\hyp \times)}`$ により反変に保存されることを絵（ストリング図）に描けば次のようです。

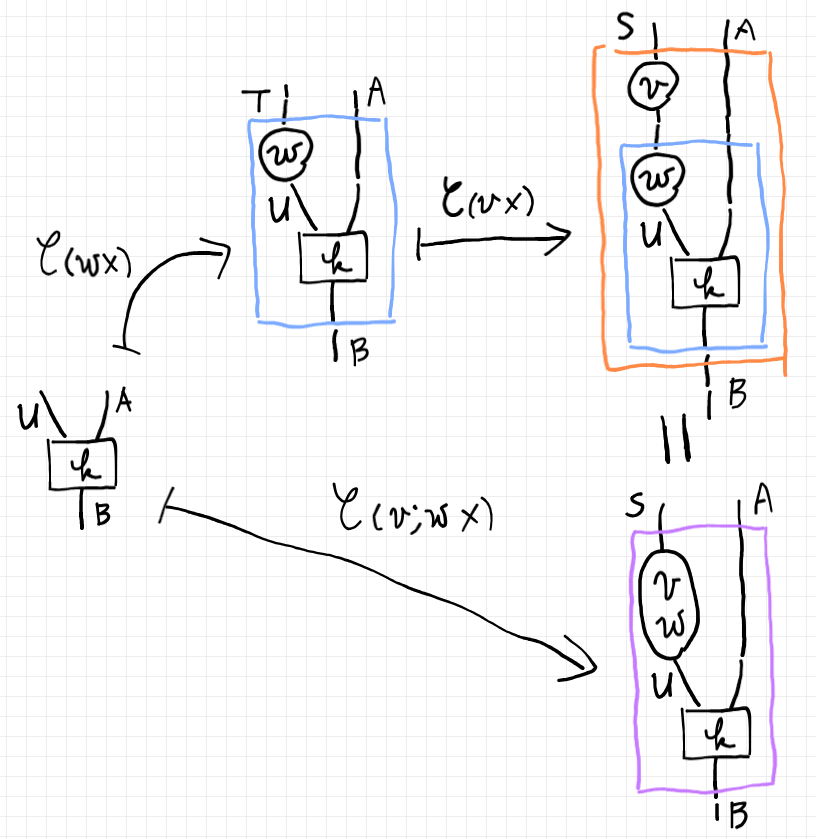
恒等射が恒等自然変換に移るのも明らかでしょう。

以上により、圏 $`\cat{C}`$ から圏 $`\dimU{\bf CAT}{1}`$ への反変関手が定義されました。

$`\quad \cat{C}_{(\hyp \times)} : \cat{C}^\mrm{op} \to \dimU{\bf CAT}{1} \In \mathbb{CAT}`$

$`\mathbb{CAT}`$ については、「変換手n-圏のブラケット記法」の冒頭とそこからリンクされている過去記事を参照してください。

圏から圏達の圏への反変関手はインデックス付き圏〈indexed category〉なので*4、$`\cat{C}_{(\hyp \times)}`$ は、$`\cat{C}`$ をインデキシング圏〈ベース圏〉とするインデックス付き圏です。

グロタンディーク構成とファイブレーション

インデックス付き圏 $`\cat{C}_{(\hyp \times)}`$ に対してグロタンディーク構成を施します。グロタンディーク構成は積分記号で書くのが習慣（「グロタンディーク構成と積分記号」参照）なので、次のように書きます*5。

$`\quad \int_{\cat{C}} \cat{C}_{(\hyp\times) } = \int_{x \In \cat{C}} \cat{C}_{(x \times) }`$

ここでは、$`\int_{\cat{C}} \cat{C}_{(\hyp\times) }`$ を一文字 $`\cat{E}`$ で表すことにします。

$`\quad \cat{E} := \int_{\cat{C}} \cat{C}_{(\hyp\times) }`$

$`\cat{E}`$ は次のような圏です。

対象： $`\cat{C}`$ の対象 $`S`$ と $`\cat{C}_{(S\times)}`$ の対象 $`A`$ のペア $`(S, A)`$
射： $`\cat{C}`$ の射 $`f_1 : S \to T`$ と $`\cat{C}_{(S\times)}`$ の射 $`f_2 : (S\times )A \to B`$ のペア $`(f_1, f_2) : (S, A) \to (T, B)`$

グロタンディーク構成の定義からは、$`\cat{E}`$ の対象 $`(S, A)`$ は依存ペアですが、環境付き計算の場合は $`|\cat{C}_{(S\times)}| = |\cat{C}|`$ だったので、依存ペアではなくて独立ペア（第一成分と第ニ成分を独立に自由に取れる）です。

$`\quad |\cat{E}| = |\cat{C}| \times |\cat{C}|`$

グロタンディーク構成における射の定義は、

$`\quad f_1 : S\to T \In \cat{C}\\
\quad f_2 : A \to \cat{C}_{(f1 \times)}(B) \In \cat{C}_{(S\times)}
`$

なのですが、$`\cat{C}_{(f_1 \times)}(B) = B`$ なので簡略化されています。$`\cat{E}`$ の射であるペア $`(f_1, f_2)`$ は次のように書きます。

$`\quad f = (f_1, f_2) =
\begin{pmatrix}
f_1 : S \to T\\
f_2 : (S\times)A \to B
\end{pmatrix} : (S, A) \to (T, B) \In \cat{E}
`$

圏 $`\cat{E}`$ の射の結合と恒等射は次のストリング図のように定義します。

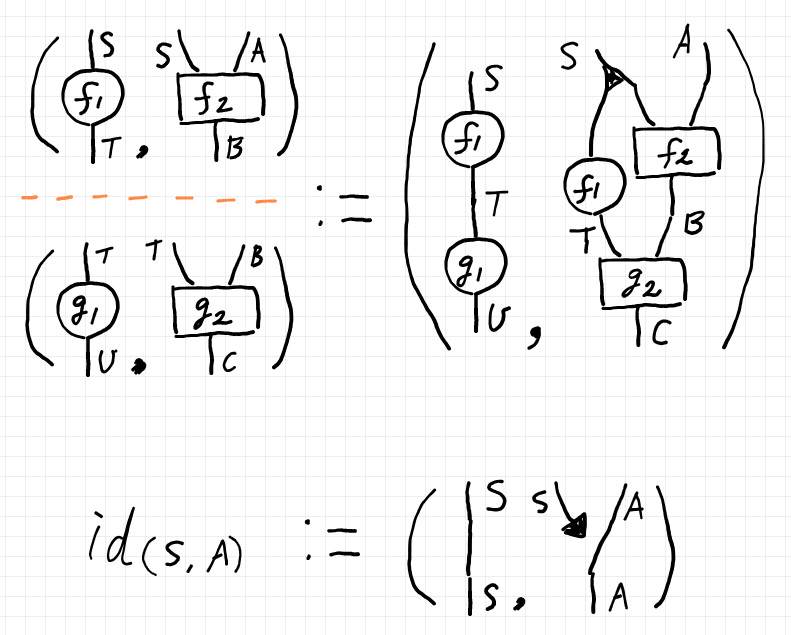
テキストで書くなら：

$`\quad (f_1, f_2) ; (g_1, g_2) := (f_1; g_1, (\Delta_S\times \id_A) ; (f_1\times f_2); g_2)\\
\quad \id_{(S, A)} := (\id_S, \pi^{S, A}_2)
`$

ここで、$`\pi^{S, A}_2`$ は直積の第二射影ですが、第二射影は終射（絵では黒い小さな三角） $`!_S`$ と左単位律子〈unitor〉 $`\lambda_A`$ で表現できます。

$`\quad \pi^{S, A}_2 = (!_S \times \id_A); \lambda_A \;: S\times A \to A \In \cat{C}`$

このように定義された射の結合と恒等射が、圏の法則〈公理〉（結合法則と左右の単位法則）を満たすことはグロタンディーク構成の一般論から保証されますが、直接的な確認もしておきましょう。絵算〈ストリング図計算〉を使えば容易に示せます。このときキモとなるのは、対角射（黒い二股分岐）と終射（黒い小さな下向き三角形）が、各対象ごとに“自然な”コモノイド構造を形成していることです。ここでの「自然な」は、コモノイドの構造射（コモノイド余乗法とコモノイド余単位）の族が自然変換になることです。

例えば結合律を示すならば、$`(f; g);h`$ と $`f;(g;h)`$ を別々に計算して：

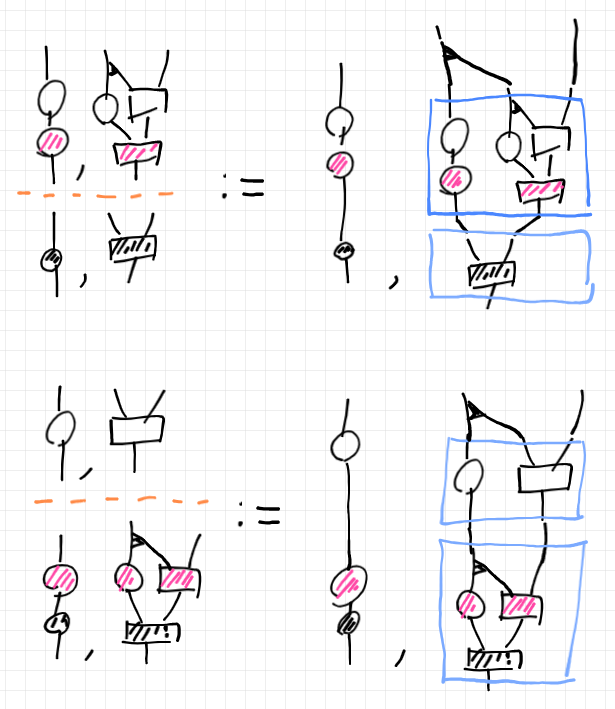
これらが等しいことは次のようにして示せます。下段は、等式的変形の根拠となる自然なコモノイド法則です。下段左は、コモノイド余乗法（黒い二股分岐）の自然性です。

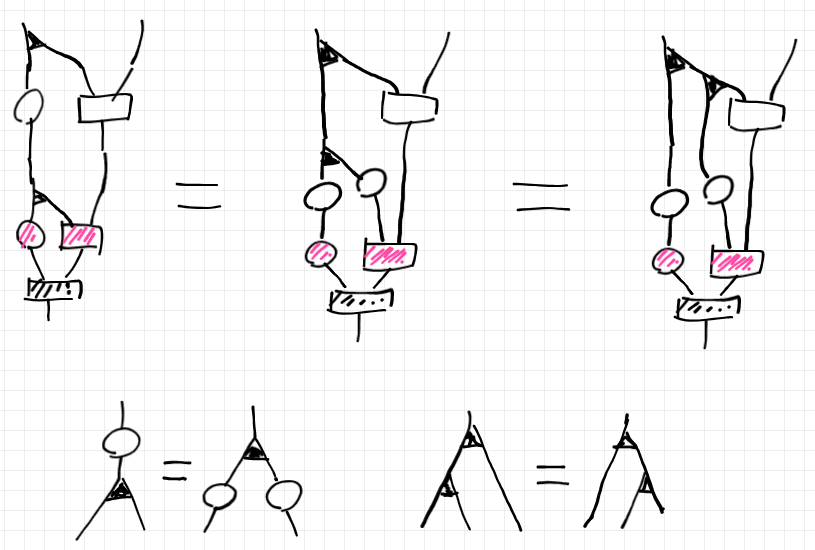
射の結合に関する左右の単位法則も、コモノイドの左右の余単位法則から示せます。

このようにして定義された圏 $`\cat{E}`$ の対象も射もペアなので、第一成分をとることが出来ます。ペアの第一成分をとる操作は関手になっています。この関手を射影関手〈projection functor〉と呼び次のように書きます。

$`\quad \mrm{Proj} :\cat{E} \to \cat{C} \In {\bf CAT}`$

対象 $`S\in |\cat{S}|`$ に対する関手 $`\mrm{Proj}`$ の逆像は、$`S`$ 上のファイバー〈fiber | fibre〉または局所圏〈local category〉と呼び、次のように書きます。

$`\quad \cat{E}_{@S} := \mrm{Proj}^{-1}(S) \; \In {\bf CAT}`$

$`\cat{E}`$ の作り方から、次が成立します。

$`\quad \cat{E}_{@S} = \cat{C}_{(S\times)} \; \In {\bf CAT}`$

$`\mrm{Proj}:\cat{E} \to \cat{C}`$ は、ファイバー付き圏〈{fibered | fibred} category〉、グロタンディーク・ファイブレーション〈Grothendieck fibration〉、あるいは単にファイブレーション〈fibration〉と呼ばれる構造になります。

ファイブレーションに関しては詳しく述べませんが、インデックス付き圏からグロタンディーク構成で作った圏とその射影関手はファイブレーションになります。ファイブレーションに関しては、次の言葉を使います。

$`\cat{C}`$ をベース圏〈base category〉と呼び、ベース圏の対象はベース対象〈base object〉、ベース圏の射はベース射〈base morphism〉と呼ぶ。
ファイバー〈局所圏〉 $`\cat{E}_{@S}`$ を垂直圏〈vertical category〉と呼ぶこともある。垂直圏の射を垂直射〈vertical morphism〉と呼ぶ。
$`\cat{E}`$ の対象／射はペアなので、第一成分をベースパート〈base part〉、第二成分をファイバーパート〈fiber part〉と呼ぶ。

依存アクテゴリー

依存アクテゴリーの正式な定義は不明ですが（「依存アクテゴリーが面白い」参照）、次のように考えてよさそうです。

依存アクテゴリーは、第一にファイブレーション〈ファイバー付き圏〉である。
それだけでなく、依存アクテゴリーは、ファイブレーションの射影を左脚とするスパンである。
それだけでなく、依存アクテゴリーは、“圏達の2-圏内のスパン達の圏”のモノイドである。

前節で $`\mrm{Proj} : \cat{E} \to\cat{C}`$ がファイブレーションであることは述べました。第一の条件はクリアです。

射影 $`\mrm{Proj}`$ を左脚として、スパンの右脚が必要です。右脚を $`\mrm{Mix}`$ とすると、スパンは次の形状です。

$`\quad \cat{C}\overset{\mrm{Proj}}{\longleftarrow} \cat{E}
\overset{\mrm{Mix}}{\longrightarrow} \cat{C} \In {\bf CAT}
`$

三番目の条件は、言い方を変えると、“圏達の2-圏"内の内部圏〈圏対象〉となっていることです。さらに言い方を変えると、依存アクテゴリーは二重圏の構造を持つ必要があります。

$`A`$ を対象の集合、$`B`$ を射の集合とする通常の圏を次のように書きましょう。

$`\quad (A, B, \mrm{dom}, \mrm{cod}, \mrm{id}, \mrm{comp})`$

今話題にしている依存アクテゴリーを同じ書き方で書くと次のようです。

$`\quad (\cat{C}, \cat{E}, \mrm{Proj}, \mrm{Mix}, \mrm{TLift}, \mrm{Coupl})`$

詳しくは後述しますが、短くコメントすると：

$`\mrm{Mix}: \cat{E} \to \cat{C} \In {\bf CAT}`$ ：環境付き計算の第一成分〈ベースパート〉と第二成分〈ファイバーパート〉を上手に混合〈mix〉したベース射（$`\cat{C}`$ の射）を構成する関手。
$`\mrm{TLift}: \cat{C} \to \cat{E} \In {\bf CAT}`$ ： $`\cat{C}`$ の対象／射に、ファイバー内の単位対象〈自明対象〉／自明な射を対応させる関手。名前は trivial lift 〈自明持ち上げ〉から。$`\mrm{Proj}, \mrm{Mix}`$ のセクション（正確にはスード・セクション）になっている。
$`\mrm{Coupl}: \cat{E} \NFProd{\mrm{Mix}}{\cat{C}}{\mrm{Proj}} \cat{E} \to \cat{E} \In {\bf CAT}`$ ： 2つの環境付き計算をカップリング〈coupling〉する。カップリングの第一項の混合〈mix〉と第二項の射影が等しいときにだけカップリングを定義可能。

これだけでは何のことか分からないでしょうが、満たすべき法則をスード可換図式として列挙しておきます。圏の法則と同じですが、等式（厳密可換図式）であることは要求していません。記号 '$`\cong`$' はスード可換性、つまり関手の自然同型が存在することを意味します。

最初の法則は $`\mrm{TLift}`$ に関するものです。

$`\quad \xymatrix@C+1pc@R+1pc{
\cat{C} \ar@{=}[d] \ar@{}[dr]|{\cong}
& \cat{C} \ar[d]|{\mrm{TLift}} \ar@{=}[l] \ar@{=}[r]
& \cat{C} \ar@{=}[d] \ar@{}[dl]|{\cong}
\\
\cat{C}
& \cat{E} \ar[l]^{\mrm{Proj}} \ar[r]_{\mrm{Mix}}
& \cat{C}
}\\
\quad \In {\bf CAT}
`$

ファイバー積 $`\cat{E} \NFProd{\mrm{Mix}}{\cat{C}}{\mrm{Proj}} \cat{E}`$ を $`\cat{E}\times_{\cat{C}}\cat{E}`$ とも書くことにして、ファイバー積を定義するプルバック図式は厳密プルバック（後述、続きの記事で）だとします。

$`\quad \xymatrix{
{}
& \cat{E} \times_\cat{C} \cat{E} \ar[dl]_{P_1} \ar[dr]^{P_2}
\ar@{}[dd]|{\text{p.b.}}
& {}
\\
\cat{E} \ar[dr]_{\mrm{Mix}}
& {}
& \cat{E} \ar[dl]^{\mrm{Proj}}
\\
{}
& \cat{C}
& {}
}\\
\quad \In {\bf CAT}
`$

法則の記述を続けます。以下は $`\mrm{Coupl}`$ に関する法則です。

$`\quad \xymatrix@R+1pc{
\cat{C} \ar@{=}[d]
\ar@{}[drr]|{\cong}
& \cat{E} \ar[l]_{\mrm{Proj} }
& \cat{E}\times_\cat{C}\cat{E} \ar[l]_{\mrm{P1} } \ar[r]^{\mrm{P_2} }
\ar[d]|{\mrm{Coupl} }
& \cat{E} \ar[r]^{\mrm{Mix}}
& \cat{C} \ar@{=}[d]
\ar@{}[dll]|{\cong}
\\
\cat{C}
& {}
& \cat{E} \ar[ll]^{\mrm{Proj} } \ar[rr]_{\mrm{Mix}}
& {}
& \cat{C}
}\\
\quad \In {\bf CAT}
`$

ここで、次のように置きます。アスタリスク '$`*`$' は関手の結合の図式順演算子記号です。セミコロンからアスタリスクに変わったのは、舞台となる圏が1-圏から2-圏に変わったからです。

$`\quad \mrm{Proj'} := \mrm{P_1}* \mrm{Proj} \;: \cat{E}\times_\cat{C} \cat{E} \to \cat{C} \In {\bf CAT}\\
\quad \mrm{Mix'} := \mrm{P_2}* \mrm{Mix} \;: \cat{E}\times_\cat{C} \cat{E} \to \cat{C} \In {\bf CAT}
`$

こう置くと、上の図式が簡略化されます。

$`\quad \xymatrix@R+1pc{
\cat{C} \ar@{=}[d]
\ar@{}[dr]|{\cong}
& \cat{E}\times_\cat{C}\cat{E} \ar[l]_{\mrm{Proj'} } \ar[r]^{\mrm{Mix'} }
\ar[d]|{\mrm{Coupl} }
& \cat{C} \ar@{=}[d]
\ar@{}[dl]|{\cong}
\\
\cat{C}
& \cat{E} \ar[l]^{\mrm{Proj} } \ar[r]_{\mrm{Mix}}
& \cat{C}
}\\
\quad \In {\bf CAT}
`$

残る法則は、二項演算 $`\mrm{Coupl}`$ の結合法則と左右の単位法則（つまりモノイド法則）です。これらの記述にはスパンの二重圏を使うのが良い方法です。次節で、スパンの二重圏のなかで結合法則と左右の単位法則を記述します。

モノイド法則

$`\mrm{Mix}, \mrm{TLift}, \mrm{Coupl}`$ の正体を先に知りたい方は、この節は飛ばしてもかまいません。必要なときに戻って読めばいいでしょう。

まず、スパンの結合の描き方を決めておきます。以下は、$`A`$ をボディ〈ヘッド〉とするスパンと $`B`$ をボディとするスパンを結合して、$`C`$ をボディとするスパンが得られたことを示す図式です。$`\text{p.b.}`$ はプルバック四角形であることを示します。

$`\quad \xymatrix {
{}
& {}
& C \ar[dl] \ar[dr]\ar@{}[dd]|{\text{p.b.}}
& {}
& {}
\\
{}
& A \ar[dl] \ar[dr]
& {}
& B \ar[dl] \ar[dr]
& {}
\\
X
& {}
& Y
& {}
& Z
}`$

このようなプルバックの結合を以下のようにも描きます。$`\text{s.c}`$ はスパンの結合（span composition）であることを示します。

$`\quad \xymatrix {
{}
& {}
& C \ar[dll] \ar[drr] \ar@{}[d]|{\text{s.c.}}
& {}
& {}
\\
X
& A \ar[l] \ar[r]
& Y
& B \ar[l] \ar[r]
& Z
}`$

さらに、$`A`$ をボディとするスパンを $`S`$ 、$`B`$ をボディとするスパンを $`T`$ として、次のようにも描きます。スパンの結合に、ファイバー積の記号 $`\times_Y`$ を流用〈オーバーロード〉しています。気になるなら他の記号、例えば $`\diamondsuit_Y`$ とかに変えてください。

$`\quad \xymatrix@C+1pc{
X \ar@{-->}[r]_S \ar@{-->}@/^1.5pc/[rr]^{S\times_Y T}
& Y \ar@{-->}[r]_T
& Z
}`$

スパンを表す矢印（破線矢印を使ってます）が繋がっている（パスになっている）のを見たら、何も書いてなくてもスパンの結合を表すと約束するならば、以下の $`X`$ から $`Z`$ に向かう破線パスは $`S`$ と $`T`$ の結合 $`S\times_Y T`$ を表します。

$`\quad \xymatrix@C+1pc{
X \ar@{-->}[r]_S
& Y \ar@{-->}[r]_T
& Z
}`$

さて、我々が注目しているスパンに名前を付けておきましょう。

$`\cat{C} \overset{\mrm{Id}_\cat{C}}{\longleftarrow} \cat{C} \overset{\mrm{Id}_\cat{C}}{\longrightarrow}\cat{C}`$ を $`\mrm{I}_\cat{C}`$ と呼ぶ。これは、$`\cat{C}`$ の恒等スパン。
$`\cat{C} \overset{\mrm{Proj}}{\longleftarrow} \cat{E} \overset{\mrm{Mix}}{\longrightarrow}\cat{C}`$ を、名前をオーバーロードして $`\cat{E}`$ と呼ぶ。ボディの名前をスパンの名前として流用する。
$`\cat{C} \overset{\mrm{Proj'}}{\longleftarrow} \cat{E}\times_\cat{C}\cat{E} \overset{\mrm{Mix'}}{\longrightarrow}\cat{C}`$ を、名前をオーバーロードして $`\cat{E}\times_\cat{C}\cat{E}`$ と呼ぶ。ボディの名前をスパンの名前として流用しているのと同時に、スパン $`\cat{E}`$ とスパン $`\cat{E}`$ のスパン結合だとも解釈できる。

以上のように約束すると、結合法則／単位法則は、図式のあいだの等式で表現できます。例えば、結合法則の左辺は次の図式になります。この図式は、2-圏 $`{\bf CAT}`$ 内のスパンの二重圏（「依存アクテゴリーが面白い」参照）における図式です。縦方向のイコール記号は恒等関手（恒等タイト射）を表します。四角形内のイコールはスパンのあいだの恒等射（恒等二重射）を表します。

同じ内容を、$`\text{s.c.}`$ を使って $`{\bf CAT}`$ 内に描くと、サイズが大きな図式となって扱いにくいです。（詳細を見たいときはメリットがありますが。）

$`\quad \xymatrix{
\cat{C} \ar@{=}[dd]
& \cat{E} \ar[l] \ar[r]
& \cat{C}
& \cat{E} \ar[l] \ar[r]
& \cat{C} \ar@{=}[dd]
& \cat{E} \ar[l] \ar[r] \ar@{=}[dd]
& \cat{C} \ar@{=}[dd]
\\
{}
& {}
& {\cat{E}\times_\cat{C}\cat{E} } \ar[d]|{\mrm{Coupl}} \ar[ull] \ar[urr]
\ar@{}[u]|{\text{s.c.}}
& {}
& {}
& {}
& {}
\\
\cat{C} \ar@{=}[dd]
& {}
& \cat{E} \ar[ll] \ar[rr]
& {}
& \cat{C}
& \cat{E}\ar[l] \ar[r]
& \cat{C} \ar@{=}[dd]
\\
{}
& {}
& {}
& {}
& {\cat{E}\times_\cat{C}\cat{E} } \ar[d]|{\mrm{Coupl}} \ar[ullll] \ar[urr]
\ar@{}[u]|{\text{s.c.}}
& {}
& {}
\\
\cat{C}
& {}
& {}
& {}
& \cat{E} \ar[llll] \ar[rr]
& {}
& \cat{C}
}\\
\quad \text{commutative }\In {\bf CAT}
`$

プルバック四角形（$`\text{p.b.}`$）まで描くと、もっとゴチャゴチャした図式になります。スパンを単一の射（プロ射）として扱うことで、煩雑さが緩和されています。ストリング図を使うとさらに可読性・視認性が向上しますが、それについては「依存アクテゴリーが面白い」のストリング図を見てください。

いよいよ結合法則です。等式は縦方向に書きます（レイアウト指定が少し楽になるという事情）。次の図の上段の図式で表現される二重射と、下段の図式で表現される二重射が等しい二重射であることを主張または要求しています。

$`\quad \xymatrix{
\cat{C} \ar@{-->}[r]^{\cat{E}} \ar@{=}[d]
\ar@{}[drr]|{\mrm{Coupl}\,\Downarrow\:}
& \cat{C} \ar@{-->}[r]^{\cat{E}}
& \cat{C} \ar@{-->}[r]^{\cat{E}} \ar@{=}[d]
\ar@{}[dr]|{=}
& \cat{C} \ar@{=}[d]
\\
\cat{C} \ar@{-->}[rr]_{\cat{E}} \ar@{=}[d]
\ar@{}[drrr]|{\mrm{Coupl}\,\Downarrow\:}
& {}
& \cat{C} \ar@{-->}[r]_{\cat{E}}
& \cat{C} \ar@{=}[d]
\\
\cat{C} \ar@{-->}[rrr]_{\cat{E}}
& {}
& {}
& \cat{C}
}\\
\quad \xymatrix{
{}
& {} \ar@{}[r]|{\mid \mid }
& {}
& {}
}\\
\quad \xymatrix{
\cat{C} \ar@{-->}[r]^{\cat{E}} \ar@{=}[d]
\ar@{}[dr]|{=}
& \cat{C} \ar@{-->}[r]^{\cat{E}} \ar@{=}[d]
\ar@{}[drr]|{\mrm{Coupl}\,\Downarrow\:}
& \cat{C} \ar@{-->}[r]^{\cat{E}}
& \cat{C}\ar@{=}[d]
\\
\cat{C} \ar@{-->}[r]_{\cat{E}} \ar@{=}[d]
\ar@{}[drrr]|{\mrm{Coupl}\,\Downarrow\:}
& \cat{C} \ar@{-->}[rr]_{\cat{E}}
& {}
& \cat{C} \ar@{=}[d]
\\
\cat{C} \ar@{-->}[rrr]_{\cat{E}}
& {}
& {}
& \cat{C}
}\\
\quad \In \mathbb{S}{\bf PAN}({\bf CAT})
`$

左単位法則は次のようです。$`\mrm{LeftUnit}`$ は、スパンの結合（二重圏ではプロ射のプロ結合）に関する左単位律子〈left unitor〉です。

$`\quad \xymatrix{
\cat{C} \ar@{-->}[r]^{\mrm{I}_\cat{C}} \ar@{=}[d]
\ar@{}[dr]|{\mrm{TLift}\,\Downarrow\:}
& \cat{C} \ar@{-->}[r]^{\cat{E}} \ar@{=}[d]
\ar@{}[dr]|{=}
& \cat{C} \ar@{=}[d]
\\
\cat{C} \ar@{-->}[r]_{\cat{E}} \ar@{=}[d]
\ar@{}[drr]|{\mrm{Coupl}\,\Downarrow\:}
& \cat{C} \ar@{-->}[r]_{\cat{E}}
& \cat{C} \ar@{=}[d]
\\
\cat{C} \ar@{-->}[rr]_{\cat{E}}
& {}
& \cat{C}
}\\
\quad \xymatrix{
{}
& {\mid \mid }
& {}
}\\
\quad \xymatrix{
\cat{C} \ar@{-->}[r]^{\mrm{I}_\cat{C}} \ar@{=}[d]
\ar@{}[drr]|{\mrm{LeftUnit}_\cat{E}}
& \cat{C} \ar@{-->}[r]^{\cat{E}}
& \cat{C} \ar@{=}[d]
\\
\cat{C} \ar@{-->}[rr]^{\cat{E}}
& {}
& \cat{C}
}\\
\quad \In \mathbb{S}{\bf PAN}({\bf CAT})
`$

右単位法則は、左単位法則の左右を逆にしたものです。

ここまでの話では、モノイドの法則は等式で与えられるとしてきました。モノイド概念を高次元化／弱化すると、モノイド法則が等式ではなくて一貫性同型射〈coherence isomorphism〉となるスードモノイド〈pseudo-monoid〉となります。ひょっとすると、モノイドでは足りなくてスードモノイドが必要となる場面があるかも知れませんが、今はスードモノイドに足を踏み入れるのはやめておきます。（[追記]いやいや、スードモノイドはすぐに必要になりますね。足を踏み入れなくちゃなりません。[/追記]）

環境付き計算ペアのミックス操作

圏 $`\cat{E}`$ の射は、次のようなペアで表現できるので、環境付き計算ペア〈computation-with-environment pair〉と呼ぶことにします。

$`\quad f = (f_1, f_2) =
\begin{pmatrix}
f_1 : S \to T\\
f_2 : (S\times)A \to B
\end{pmatrix} : (S, A) \to (T, B) \In \cat{E}
`$

ミックス〈mix | 混合〉は、与えられた環境付き計算ペアのベースパートとファイバーパートを混ぜて、ベース射（圏 $`\cat{C}`$ の射）を作り出す操作です。次のように定義します。

$`\text{For }f = (f_1, f_2) : (S, A) \to (T, B)\\
\quad \mrm{Mix}(f) = \mrm{Mix}( (f_1, f_2) ) := (\Delta_S\times \id_A);(f_1 \times f_2)
`$

絵で描けば次のようです。

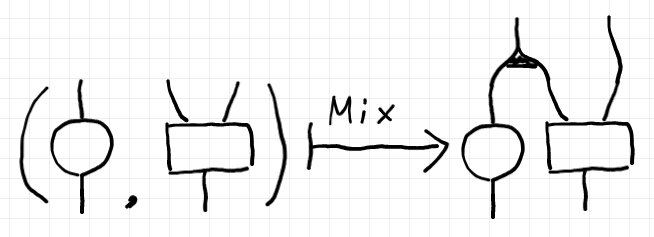
記述を簡潔にするために、一種の中置演算子記号 '$`\triangle`$' を導入します。

$`\quad f_1 \triangle f_2 := \mrm{Mix}( (f_1, f_2) )`$

$`\triangle`$ の左右の項は、環境付き計算ペアのベースパートとファイバーパートです。自由に引数を選べるわけではありません。

さて、$`\mrm{Mix}`$ を、圏 $`\cat{E}`$ から圏 $`\cat{C}`$ への関手として定義しましょう。以下のようです。

$`\text{For }(S, A) \in |\cat{E}|\\
\quad \mrm{Mix}( (S, A) ) := S\times A \; \in |\cat{C}|\\
\text{For } (f_1, f_1) : (S, A) \to (T, B) \In \cat{E}\\
\quad \mrm{Mix}( (f_1, f_2) ) := (f_1 \triangle f_2 : S\times A \to T\times B \In \cat{C})
`$

$`\mrm{Mix}`$ が関手であるためには、関手性（結合の保存と恒等射の保存）が必要です。

$`\text{For }f: (S, A) \to (T, B), g:(T, B) \to (U, C) \In \cat{E}\\
\quad \mrm{Mix}(f ; g) = \mrm{Mix}(f) ; \mrm{Mix}(g)\\
\text{For }(S, A) \in |\cat{E}|\\
\quad \mrm{Mix}( \id_{(S, A)} ) = \id_{S\times A}
`$

結合の保存は、次の図で示せます。

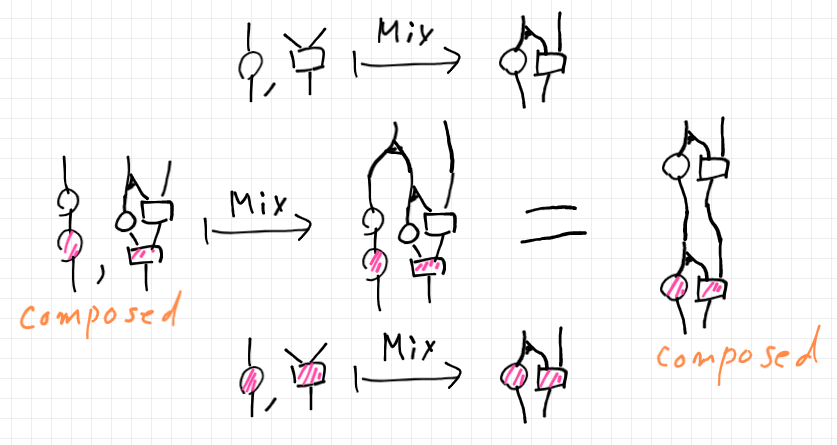
$`f`$ が白で $`g`$ がピンクだとします。$`f`$ のミックスを上段、$`g`$ のミックスを下段に描いています。中段左は、$`\cat{E}`$ 内での結合 $`f; g`$ です。中段右は、 $`\cat{C}`$ 内での結合 $`\mrm{Mix}(f); \mrm{Mix}(g)`$ です。中段の等式が結合の保存を意味しますが、この等式を絵の変形で証明することはもう大丈夫でしょう。

恒等射の保存は、次の図で示せます。

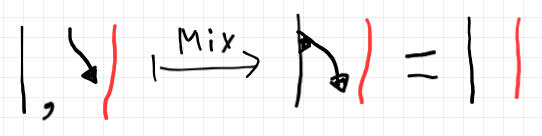
等式の根拠は、コモノイドの右余単位法則です。

以上で、$`\mrm{Mix}`$ が圏 $`\cat{E}`$ から圏 $`\cat{C}`$ への関手であることが分かりました。

ファイブレーションの射影関手 $`\mrm{Proj}`$ と一緒にすると、圏達の2-圏 $`{\bf CAT}`$ のなかのスパンが出来上がりました。

$`\quad \xymatrix{
\cat{C}
& \cat{E} \ar[l]_{\mrm{Proj}} \ar[r]^{\mrm{Mix}}
& \cat{C}
}
\; \In {\bf CAT}
`$

これは、圏達の2-圏のなかのスパン達の二重圏 $`\mathbb{S}{\bf PAN}({\bf CAT})`$ のプロ射でもあります。名前 $`\cat{E}`$ をオーバーロードして次のように書きます。

$`\quad \xymatrix{
\cat{C} \ar@{-->}[r]^{\cat{E}}
& \cat{C}
}
\; \In \mathbb{S}{\bf PAN}({\bf CAT})
`$

さてところで、中置演算子記号 '$`\triangle`$' を $`\mrm{Mix}`$ の完全な別名として使用すると便利なので、今後そうします。$`f_1 \triangle f_2 := \mrm{Mix}( (f_1, f_2) )`$ 以外に、次の約束もします。

$`\text{For }(S, A) \in |\cat{E}|\\
\quad S \triangle A := \mrm{Mix}( (S, A) ) = S\times A \;\in |\cat{C}|
`$

対象に対しては、$`\triangle`$ と $`\times`$ は同じ演算だと約束するわけです。

こうすると、次のように書けます。

$`\quad (\triangle) : \cat{E} \to \cat{C} \In {\bf CAT}`$

ミックス $`(\triangle)`$ が（例えば $`(\bullet)`$ と書くような）アクテゴリーの作用〈action〉の類似物であることが強調されます。

ベース射の自明持ち上げ

ファイブレーション $`\mrm{Proj}:\cat{E} \to \cat{C}`$ において、$`\cat{C}`$ の射はベース射と呼ぶのでした。ベース射を、$`\cat{E}`$ の射、つまり環境付き計算ペアへと持ち上げましょう。「持ち上げ」とは、射影するともとに戻るようにファイバーパートを選ぶことです。

次のような写像を考えます。以下の $`\mrm{I}`$ はデカルト圏 $`\cat{C}`$ の終対象兼モノイド単位対象です。

$`\text{For }v:S \to T \In \cat{C}\\
\quad \mrm{TLift}(v) := (v, \pi^{S\times \mrm{I}}_2) : (S\times)\mrm{I} \to \mrm{I}
`$

$`\mrm{TLift}(v)`$ を、ベース射 $`v`$ の自明持ち上げ〈trivial lift〉と呼びましょう。定義から、$`\mrm{Proj}(\mrm{TLift}(v)) = v`$ が言えます。

$`\mrm{TLift}`$ を絵で描けば次のようです。

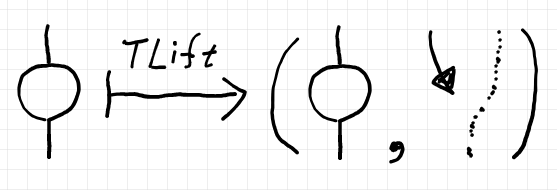
点線は $`\mrm{I}`$ と $`\id_{\mrm{I}}`$ を表します。

次のように定義すれば、$`\mrm{TLift}`$ は関手になります。

$`\text{For }S \in |\cat{C}|\\
\quad \mrm{TLift}(S ) := (S, \mrm{I}) \; \in |\cat{E}|\\
\text{For } v:S \to T \In \cat{C}\\
\quad \mrm{TLift}(v) := ( (v, \pi^{S\times \mrm{I}}_2) : (S\times)\mrm{I} \to \mrm{I} \In \cat{E})
`$

$`\mrm{TLift}`$ が関手であるためには、関手性（結合の保存と恒等射の保存）が必要です。

$`\text{For }v: S \to T, w:T \to U, C \In \cat{C}\\
\quad \mrm{TLift}(v ; w) = \mrm{TLift}(v) ; \mrm{TLift}(w)\\
\text{For }S \in |\cat{C}|\\
\quad \mrm{TLift}( \id_S ) = \id_{(S, \mrm{I})}
`$

結合の保存は以下のような等式を示せばよいのですが、もう明らかでしょう。

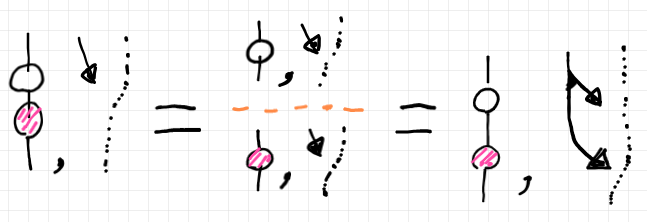
恒等射の保存は、$`\id_{(S, \mrm{I})}`$ の定義そのものです。

以上で、$`\mrm{TLift}`$ が $`\cat{C}`$ から $`\cat{E}`$ への関手であることが分かりました。

自明持ち上げの法則

$`\mrm{TLift} * \mrm{Proj} = \mrm{Id}_{\cat{C}}`$ は、（そうなるように定義したので）成立します。では、$`\mrm{TLift} * \mrm{Mix}`$ はどうなるでしょうか？計算してみます。

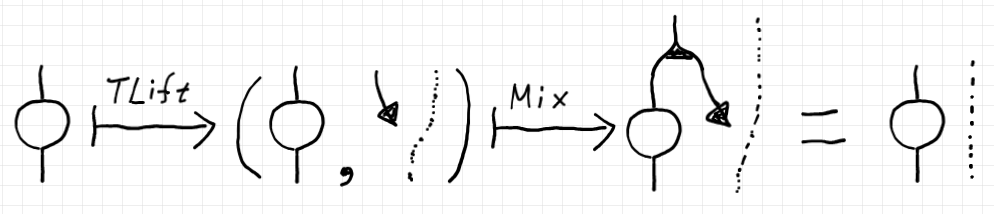
つまり、次のような結果になります。

$`\quad \mrm{TLift} * \mrm{Mix} = (\hyp \times \mrm{I}) \;: \cat{C}\to \cat{C} \In {\bf CAT}`$

$`\mrm{TLift} * \mrm{Mix}`$ は、厳密に $`\mrm{Id}_{\cat{C}}`$ にはなりませんが、モノイド単位対象を（デカルト積の意味で）掛け算するだけなので、“ほとんど恒等関手”のようなものです。次の自然同型が成立します。

$`\quad \mrm{TLift} * \mrm{Mix} \cong \mrm{Id}_\cat{C} \;: \cat{C}\to \cat{C} \In {\bf CAT}`$

「依存アクテゴリー」の節で提示した自明持ち上げ（$`\mrm{TLift}`$）に関する法則は次でした。

これは、$`\cong`$ を自然同型として次を意味します。

$`\mrm{TLift} * \mrm{Proj} \cong \mrm{Id}_\cat{C} \In {\bf CAT}`$
$`\mrm{TLift} * \mrm{Mix} \cong \mrm{Id}_\cat{C} \In {\bf CAT}`$

どちらも成立します。これは、$`\mrm{TLift}`$ がスパンとしての $`\cat{E}`$ のセクション（正確にはスード・セクション）になっているということです。

2-圏内のスパンのあいだの射

ここでちょっと一般論をはさみます。

1-圏であれ2-圏であれ、スパンの定義はハッキリしています。ひとつの対象〈0-射〉から出る2本の射のことですから。プルバック（「ファイバーの計算の動機としてのプルバック公式 // プルバックってなに？」参照）を使ったスパンの結合〈横結合〉や、2つのスパンのあいだの射も、1-圏ならハッキリした概念です。

しかし、2-圏におけるスパンの結合や、2つのスパンのあいだの射は、色々なバリエーションがあります（その事情は「依存アクテゴリーに向けて // 一貫性地獄」参照）。一般的に、2-圏における2つのスパンのあいだの射は次の形をしています。

$`\quad \xymatrix{
\cdot \ar[d]
\ar@{}[dr]|{\alpha}
& \cdot \ar[l] \ar[r] \ar[d]
\ar@{}[dr]|{\beta}
& \cdot \ar[d]
\\
\cdot
& \cdot \ar[l] \ar[r]
& \cdot
}`$

ここで、$`\alpha, \beta`$ は四辺形（「圏論におけるフレーム充填問題 // n辺形とn角形」参照）を埋める2-射です。この $`\alpha, \beta`$ の緩さ〈looseness | weakness〉と方向にバリエーションがあるのです。上下左右は上の図のとおりとして、左の四角形の緩さと方向を表にすると：

緩さ	方向
厳密	指定不要
スード	指定不要
ラックス	左上から右下
ラックス	右下から左上

スパンの射では左右2つの四角形があり、左右で異なる緩さ・方向を要求することもあります。例えば、左四角形は厳密で、右四角形は左下から右上へのラックスとか。

この記事では、スパンのあいだの射として左右の四角形はともにスード可換であるという定義を採用しました。が、これが適切かどうかは今のところ分かりません。暫定的な定義です。カプチ／マイヤースの定義では、右四角形はラックス可換にしているようです。

このまま続けると、ひとつの記事としては長すぎるでしょう。数式・図式がたくさんあるので重いWebページになってしまいます。別記事にして続きを書きます。

続きは環境付き計算と依存アクテゴリー 2/n

*1:スタンピングにも「コ」を付けているのは語呂合わせで、デカルト積で掛け算する操作に変わりはありません。が、余クライスリ射では域側にスタンピングするので、余域側のスタンピングの双対だとも言えます。

*2:$`\cat{C}_{(S\times)}`$ という書き方の由来： $`G`$ が $`\cat{C}`$ 上のコモナドのとき、コモナドの余クライスリ圏を $`\cat{C}_G`$ と書くことがあります。$`G = (S \times \hyp) = (S\times)`$ （左から $`S`$ を掛けるコスタンピング・コモナド）と置くと、その余クライスリ圏は $`\cat{C}_{(S\times)}`$ となります。

*3:僕は、2-圏としての $`{\bf CAT}`$ における関手の結合〈横結合〉にはアスタリスクを使っています。

*4:正確に言えば、厳密インデックス付き圏です。弱インデックス付き圏もあり、弱インデックス圏はスード・インデックス付き圏、ラックス・インデックス付き圏、反ラックス・インデックス付き圏に分類されます。

*5:エンド／コエンドも積分記号で書く習慣ですが、ここではエンド／コエンドは出てこないのでコンフリクトの心配はありません。