モノイドを対象がひとつだけの圏とみなすと、両側モノイド作用(モノイドの双作用)はプロ関手だとみなせます。この種のプロ関手のコエンドは、一般の場合より簡単に構成できて、より具体的な表示を持ちます。$`\newcommand{\mrm}[1]{ \mathrm{#1} }
\newcommand{\In}{\text{ in }}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\u}[1]{\underline{#1}}
\newcommand{\o}[1]{\overline{#1}}
\newcommand{\hyp}{\text{-} }
\newcommand{\id}{\mathrm{id} }
%\newcommand{\twoto}{\Rightarrow }
\newcommand{\op}{\mathrm{op} }
\newcommand{\Imp}{\Rightarrow }
\newcommand{\lact}{\triangleright }
\newcommand{\ract}{\triangleleft }
\require{color} % 緑色
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }%
\newcommand{\For}{\Keyword{For } }%
`$
内容:
圏としてのモノイド
$`M = (\u{M}, \cdot, e)`$ をモノイドとします。$`\u{M}`$ は台集合です。これを次のような圏と考えます。
- $`\mrm{Obj}(M) = |M| := \{\star\}`$
- $`\mrm{Mor}(M) := \u{M}`$
- $`(\hyp \,; \hyp) := (\hyp \cdot \hyp)`$
- $`\id_\star := e`$
- $`\mrm{dom}, \mrm{cod}`$ は自明
'$`\cdot`$' を反図式順結合記号とみなす(つまり、 $`(\hyp \circ \hyp) := (\hyp \cdot \hyp)`$ とする)ほうが多数派でしょう。が、これは好みの問題なので、僕は図式順結合記号とみなします。
反対モノイドを $`M^\op`$ とします。「状態遷移系としての前層・余前層・プロ関手 // 捻じれ対のテキスト表示と図示」で述べたように、$`a\in \mrm{Mor}(M)`$ に対応する $`\mrm{Mor}(M^\op)`$ の要素を $`\o{a}`$ と書きます。$`a = \o{a}`$ ですが、上線は混乱を避ける効果があります。上線が目障りなら無視してください。
反対モノイド $`M^\op`$ は次のように書けます。
$`\quad M^\op = (\u{M^\op}, \o{\cdot}, \o{e})`$
$`\u{M^\op} = \u{M},\; \o{e} = e`$ ですが、反対のモノイド演算 $`\o{\cdot}`$ は $`\cdot`$ とは違います。次が成立します。
$`\For a, b \in \u{M}\\
\quad \o{a\cdot b} = \o{b} \o{\cdot} \o{a}
`$
左右のオペランドをスワップしてから $`\cdot`$ に入れる二項演算が $`\o{\cdot}`$ です。
「層化ストリング図 // 裏返し反変関手」で導入した $`\mrm{Rev}`$ を使うと:
$`\mrm{Rev}_M : M \to M^\op\\
\For a, b \in \u{M}\\
\quad \mrm{Rev}_M(a\cdot b) = \mrm{Rev}_M(b) \o{\cdot } \mrm{Rev}_M(a)
`$
$`\mrm{Rev}_M`$ は、写像としては単なる恒等写像です。$`\mrm{Rev}_M`$ は通常の意味の関手(あるいはモノイド準同型写像)ではありませんが、$`M`$ と $`M^\op`$ を結ぶには必要です。
$`M^\op \times M`$ の要素〈射〉は、「状態遷移系としての前層・余前層・プロ関手 // 捻じれ対のテキスト表示と図示」で述べた捻じれ対〈twisted pair〉なので、次のように書きます。
$`\For a, b \in \u{M}\\
\quad (\o{a}, b) \in \u{M^\op \times M} = \u{M^\op} \times\u{M} = \u{M} \times\u{M}
`$
捻じれ対の結合〈モノイド演算〉を $`\odot`$ と書くことにすると、次のように定義できます。
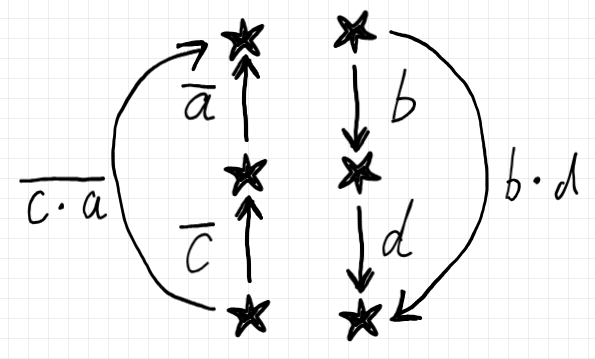
$`\quad (\o{a}, b) \odot (\o{c}, d) := (\o{c\cdot a}, b \cdot d) = ( \o{a}\o{\cdot}\o{c}, b \cdot d)`$
モノイド上のプロ関手
「状態遷移系としての前層・余前層・プロ関手」で述べたことを、特にモノイド〈単対象圏〉について再度述べます。
次のような関手を、$`M`$ 上のプロ関手〈profunctor〉と呼びます。
$`\quad P : M^\op \times M \to {\bf Set} \In {\bf CAT}`$
$`P(\star)`$ は特定の集合なので、以下 $`X`$ と書きます。
$`\quad X := P(\star) = P_\mrm{obj}(\star) \; \in |{\bf Set}|`$
$`P`$ が関手であることは次のように書けます。
$`\For (\o{a}, b), (\o{c}, d) \in \u{M^\op}\times \u{M}\\
\quad P(\, (\o{a}, b)\odot (\o{c}, d)\,) = P(\, (\o{a}, b)\,) \,;P(\, (\o{c}, d)\,)
= P(\, (\o{c}, d)\,)\circ P(\, (\o{a}, b)\,)
\quad P(\, (\o{e}, e)\,) = \id_{X}
`$
$`(\o{a}, b)\odot (\o{c}, d) = (\o{c \cdot a}, b \cdot d)`$ を使えば次のようにも書けます。
$`\For (\o{a}, b), (\o{c}, d) \in \u{M^\op}\times \u{M}\\
\quad P(\, (\o{c}, d)\,)\circ P(\, (\o{a}, b)\,) = P(\, (\o{c \cdot a}, b \cdot d)\,)\\
\quad P(\, (\o{e}, e)\,) = \id_{X}
`$
集合 $`X = P(\star)`$ の要素を取って具体的に記述すると:
$`\For (\o{a}, b), (\o{c}, d) \in \u{M^\op}\times \u{M}\\
\For x \in X\\
\quad (P(\, (\o{c}, d)\,)\circ P(\, (\o{a}, b)\,))(x) = P(\, (\o{c \cdot a}, b \cdot d)\,)(x)\\
\quad P(\, (\o{e}, e)\,)(x) = x
`$
視認性が良くないので、$`\beta(\o{a},x, b) := P(\,(\o{a}, b)\,)(x)`$ のように置きます。すると:
$`\For (\o{a}, b), (\o{c}, d) \in \u{M^\op}\times \u{M}\\
\For x \in X\\
\quad \beta(\o{c}, \beta(\o{a}, x, b), d) = \beta(\o{c \cdot a} ,x, b\cdot d)\\
\quad \beta(\o{e}, x, e) = x
`$
プロ関手を両側モノイド作用とみなす
集合 $`X`$ と写像 $`\beta(\hyp, \hyp, \hyp)`$ はプロ関手 $`P`$ から前節のように作られたものだとします。さらに、次の記法を導入します。
$`\For a, b\in \u{M}\\
\For x \in X\\
\quad a\lact x \ract b := \beta(\o{a}, x, b)
`$
この記法を使うと、$`P`$ の関手性は次のように書けます。
$`\For a, b, c, d \in \u{M}\\
\For x \in X\\
\quad c \lact ( a \lact x\ract b)\ract d = (c \cdot a)\lact x\ract (b\cdot d)\\
\quad e \lact x\ract e = x
`$
これは、モノイド $`M`$ が、集合 $`X`$ に左右両側から作用している構造です。両側モノイド作用〈two-sided monoid action〉とかモノイドの双作用〈biaction〉と呼びます。
右側に単位元を置くと左作用〈left action〉が得られます。
$`\For a \in \u{M}\\
\For x \in X\\
\quad a \lact x := a \lact x\ract e
`$
同様に、左側に単位元を置いて右作用 $`x\ract b`$ が得られます。
両側群作用のコエンド
群は、すべての要素〈射〉が逆元〈逆射〉を持つモノイドとして定義されます。両側群作用は、モノイドが特に群である場合の両側モノイド作用です。$`G`$ は群として、群が双作用する集合 $`X`$ と作用の記号 $`\lact, \ract`$ は前節と同じとします。両側群作用は、プロ関手 $`P`$ から誘導されているとします*1。
群の場合は、両側作用〈プロ関手〉のコエンドが、群の特性により単純になります。コエンドは、集合 $`X`$ を“とある同値関係”で割った商集合です。
$`x, y\in X`$ に対して、次の等式が成立するとき、$`x \sim_a y`$ と書くことにします。
$`\quad a^{-1} \lact x \ract a = y \:\text{ where }a \in \u{G}`$
等式の左辺は、群の内部自己同型〈inner automorphism 〉と類似しています。
次は容易に示せます。
$`\For x, y, z\in X\\
\quad x \sim_e x\\
\quad x \sim_a y \Imp y\sim_{a^{-1}} x\\
\quad x \sim_a y, y \sim_b z \Imp x \sim_{a\cdot b} z
`$
$`X`$ 上の関係 $`\simeq`$ を次のように定義します。
$`\For x, y\in X\\
\quad x \simeq y :\Leftrightarrow \exists a \in \u{G}. x \sim_a y
`$
関係 $`\simeq`$ は同値関係なので、商集合 $`X/\!\simeq`$ を作れます。この商集合を、両側群作用〈プロ関手〉のコエンドと定義します。
$`\quad \mrm{coend}(P) := X/\!\simeq`$
この定義が、プロ関手のコエンドの一般的な定義と一致することはこの後で示します。
コエンドの一般的な定義から
$`\cat{C}`$ を、モノイドや群とは限らない一般的な圏だとします。$`P`$ は次のようなプロ関手とします。
$`\quad P : \cat{C}^\op \times \cat{C} \to {\bf Set} \In {\bf CAT}`$
$`P`$ のコエンドは、おおざっぱに言えば、次の図式が示す余等化子〈コイコライザー〉です。
$`\quad
\xymatrix{
{\displaystyle \coprod_{f:X \to Y} P(Y, X) }\ar@/^/[r]^{L} \ar@/_/[r]_{R}
& {\displaystyle \coprod_{X} P(X, X)} \ar[r]^{\pi}
& {\displaystyle \int^{X} P(X, X)}
}
`$
この図式はおおざっぱ過ぎてよく分からないですよね。次の記事で説明しています。
また、等化子〈イコライザー〉/余等化子〈コイコライザー〉の普遍構成からの説明が次の記事にあります。
この記事では、一般論ではなくて、圏 $`\cat{C}`$ がモノイドの場合だけを考えます。プロ関手 $`P`$ が、モノイド $`M`$ による両側作用のときは次のように簡略化できます。
$`\quad
\xymatrix{
{\displaystyle \coprod_{a:\star \to \star} P(\star, \star) }\ar@/^/[r]^{L} \ar@/_/[r]_{R}
& {\displaystyle \coprod_{\star} P(\star, \star)} \ar[r]^{\pi}
& \mrm{coend}(P)
}
`$
$`\u{M}`$ と $`X`$ を使って書けば:
$`\quad
\xymatrix{
{\displaystyle \coprod_{a \in \u{M}} X }\ar@/^/[r]^{L} \ar@/_/[r]_{R}
& X \ar[r]^-{\pi}
& \mrm{coend}(P)
}
`$
左端の総和は、定数値 $`X`$ を $`\u{M}`$ 分だけ総和しているので、掛け算〈直積〉に直せます。
$`\quad
\xymatrix {
\u{M} \times X \ar@/^/[r]^{L} \ar@/_/[r]_{R}
& X \ar[r]^-{\pi}
& \mrm{coend}(P)
}
`$
これでだいぶ簡単になりました。$`\mrm{coend}(P)`$ と $`\pi`$ は、単純に $`L, R`$ の余等化子〈コイコライザー〉です。$`L`$ (左作用)と $`R`$ (右作用)は次のように定義します。
$`\For a\in \u{M}\\
\For x \in X\\
\quad L(a, x) := a\lact x = a\lact x \ract e\\
\quad R(a, x) := x\ract a = e\lact x \ract a
`$
余等化子を定義するための関係を $`X`$ 上に定義します。
$`\For x , y \in X\\
\For a \in \u{M}\\
\quad x \sim_a y :\Leftrightarrow \exists s \in X.\, x = a\lact s \land y = s \ract a
`$
図に描けば:
$`\xymatrix {
{} & s \ar@{|->}[dl]_{a\lact} \ar@{|->}[dr]^{\ract a}
& {}\\
x & {\sim_a} & y
}`$
モノイドが群のときは、$`a^{-1}`$ を使って群の場合の $`x \sim_a y`$ の定義が出てきます。群とは限らないモノイドの場合は、逆元は使えません。
モノイドの場合は $`\sim_a`$ 達がただちに同値関係にはなってくれません。同値関係 $`\simeq`$ を生成するには次の手順が必要です。
- すべての $`x\in X`$ に対して、$`x \simeq x`$ とする。
- $`x \sim_a y`$ が成り立っているとき、$`x \simeq y`$ とする。
- $`x \sim_a y`$ が成り立っているとき、$`y \simeq x`$ とする。
これで反射的・対称的関係が作れます。さらに反射的・対称的関係の推移閉包〈transitive closure〉を作ると同値関係になります。できた同値関係を $`\simeq`$ として:
$`\quad \mrm{coend}(P) := X/\!\simeq`$
グラフの連結成分の集合として
前節の商集合 $`X/\!\simeq `$ と本質的には同じことですが、あるグラフの連結成分としてコエンドを構成してみます。幾分か幾何的フレーバーが追加されます。
前節と同じセッティングで、次の集合を考えます。
$`\quad E := \{ (x, s, a, y) \in X \times X\times \u{M}\times X \mid x = a\lact s \land y = s \ract a \}`$
2つの写像 $`\mrm{src}, \mrm{trg}`$ を次のように定義します。
$`\mrm{src}, \mrm{trg} : E \to X \In {\bf Set}\\
\For (x, s, a, y) \in E\\
\quad \mrm{src}(\,(x, s, a, y)\,) := x \;\in X\\
\quad \mrm{trg}(\, (x, s, a, y)\,) := y \;\in X
`$
$`(X, E, \mrm{src}, \mrm{trg})`$ は有向グラフとなります(頂点集合が $`X`$ 、辺集合が $`E`$ 、始点・終点が $`\mrm{src}, \mrm{trg}`$)。
有向グラフを幾何的に考えると、点と線分からなる図形です。線分には向きがありますが、向きは一旦忘れます。頂点 $`x`$ から頂点 $`y`$ に向かうパス(辺を逆向きに進んでもいい)があれば、$`x, y`$ は同じ連結成分に含まれます。連結成分は、「パスで結べる」という同値関係の同値類です。
前節の商集合 $` X/\!\simeq`$ は、この節で作ったグラフの連結成分の集合です。
おわりに
プロ関手のコエンドの構成には、抽象的でけっこう煩雑な手順が使われます。一般の圏の代わりにモノイドを考えると、対象を考える必要がなくなるので構成は簡略になります。モノイドの場合を具体的に理解しておけば、たくさんの対象がある場合に一般化するのは割りと楽だと思います。
モノイド上のプロ関手は、両側作用を持つ集合、つまり両側状態遷移系です。モノイドが一般の圏になっても、状態空間がたくさんあり、異なる状態空間のあいだを飛び移れる両側状態遷移系と解釈できます(「状態遷移系としての前層・余前層・プロ関手」参照)。そう考えれば、モノイドの場合から一般の場合へと大きなギャップなく移行できるでしょう。
*1:プロ関手 $`P`$ を、両側群作用から構成することもできます。