昨日、DOTN二号(このネーミングはどうなのよ?)の話をしたのですが、DOTNのような絵図ペースの計算法により、僕はナントカ圏論の計算を追いかけることが出来てます(いやっ、出来ないこともママあるけどね^^;)。小学校の「余りのある割り算」あたりで挫折したくらいなので、僕は計算が苦手なのですが、絵を眺めていじるのは楽しい感じがします。
- Using graphical notations is undoubtedly joyful. (by Pierre-Louis Curien)
DOTN(Diagrammatic-Order Text Notation)は Text Notation ですが、絵をひたすらストレートに写しとることを目的としているので、慣れれば絵をイメージできて、絵とほぼ等価に操作できます。
絵算(pictorial/graphical/diagrammatic calculation)が万能だとは主張しません。実際、サッパリ絵に描けない状況もあります。しかし、絵算がうまくハマる状況(トラブルで嵌るじゃないよ)では劇的に計算が簡単になります。記号計算と絵算の労力が大差ないときでも、絵のほうが記憶負担が小さい(印象に残りやすい)こともあります。
以下で絵算と言っているのは2次元のストリング図の操作で、主に自然変換の計算をします。言葉を変えると、小さい圏を対象とする2-圏Catのなかでの縦方向/横方向(vertical/horizontal)の計算です。このセッティングは、絵算がうまくハマる状況のひとつです*1
今述べた状況で、キュリアの絵算とDOTN二号を、その背景と考え方を含めて紹介します。
内容:
ズボラ・イイカゲンの精神
圏論の計算は抽象度が高くそれなりに複雑です。こういうことをキマジメにやったら大変なのは当たり前です。手早くやるには、細かいことを気にせずズボラでイイカゲンにやる必要があります。「それはアンマリだろう」というくらいの手抜きをしないと、劇的に簡単にするのは無理です。
典型的なズボラ・イイカゲンさの例は、圏の対象Xとその恒等射idXを同じ記号Xで表してしまうことです。記号の乱用ですが、これは重要なテクニックです。「圏論番外:横着者のための型なし圏論(ただしフォーマル)」では、言い訳がましい理屈をこねてますが、もっと前向き積極的に「有効な技法」として使っていいのですよ。
以下で出てくる技法も、本来は違うものを区別しない、同じ記号や絵で表してしまう、というものです。もちろん、最初は違いをキッチリ理解する必要があるのですが、「違っているけど似てる」ことに気付いたら、同一視して扱ったほうが楽ちんになるのです。
種類が多すぎる!
圏論の計算で相手にするモノ(オペランド)にはたくさんの種類があります。常識的な分類で5種類ありますね。
- 圏の対象
- 対象のあいだの射
- 圏
- 圏のあいだの関手
- 関手のあいだの自然変換
DOTNでは、いちいち前置きや説明なしで種類を判別できるような約束をしています。(「自然変換の計算法 DOTN二号」に約束が書いてあります。)
- 対象: a, b
- 射:f:a→b
- 圏: A, B
- 関手: F:A→B
- 自然変換:α::F⇒G:A→B
それにしても5種類は多い。せめて3種類に; なぜなら、平面に描く絵算(2次元のストリング図)では3種類のピースしか使えないからです。点(0次元)、線(1次元)、面(2次元)です。
通常は、圏を面、関手を線、自然変換を点(実際は丸印)で描きます。次元が逆転しているのは、ストリング図ではポアンカレ双対を取るからです。このままでは対象と射を描くことができないのですが、キュリアの“格上げ”により、「対象→関手、射→自然変換」と置き換えれば、対象を線、射を点(丸印)として描けます。
5種類を3種類に還元したことにおいて、キュリアの格上げは画期的なアイデアだと思います。「恒等を作る」というのも一種の格上げで、「キュリアの格上げ」と「恒等を作る格上げ」を使うと、5階層に分かれていたモノドモを、最上位の階層、つまり自然変換として揃えることができます。あらゆるモノを自然変換とみなせるってことです。演算も縦結合「;」と横結合「*」の二種類だけになります。
キーとなる格上げ操作について次節で詳説しましょう。
格上げ操作
「対象→関手、射→自然変換」という格上げは、「対象と射を関手と自然変換に格上げする方法」で説明しています。チルダ記号を使って、対象aの格上げを a~(これは関手)、射fの格上げを f~(これは自然変換)と書きます。
それとは別に、対象、圏、関手の恒等をハット記号(サーカムフレックス)で表します。a^ は恒等射、A^ は恒等関手、F^ は恒等自然変換です。
これらの格上げを表にまとめておきましょう。f:a→b in A、F:A→B とします。また、Eは単位圏(対象1個と恒等射だけの圏)です。
| ハット格上げ | チルダ格上げ | |
| 対象a | 射 a^:a→a | 関手 a~:E→A |
| 射f | 自然変換 f~::a~⇒b~:E→A | |
| 圏A | 関手 A^:A→A | |
| 関手F | 自然変換 F^::F⇒F:A→B |
五段の階層構造を考えると、ハット格上げが一段階の昇格、チルダ格上げは三段階のゴボウ抜き昇格になる点に注意してください。
すべてのモノを最上位である自然変換に揃えるには次のように格上げします。
- 対象 a を、a~^::a~⇒a~:E→A (a~^ = a^~)
- 射 f:a→b を、f~::a~⇒b~:E→A
- 圏 A を、A^^::A^⇒A^:A→A
- 関手 F:A→B を、F^:F⇒F:A→B
格上げの雰囲気を絵にすると:
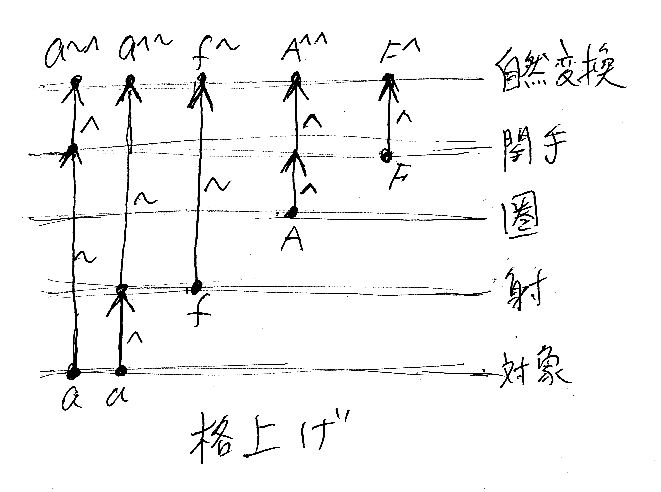
細かい印はメンドクセー
息切れしてきたので、残りは「その(2)」にしようと思います(とか言って大丈夫か?)が、冒頭に述べた「ズボラ・イイカゲンの精神」の活かし方に触れておきます。
厳密に言えば、いやっ、常識的に言えば、対象a、射a^、関手a~、自然変換a~^ は違うものです(a~^ と a^~ は同じ)。しかし、どれも似たような働きをするので、いちいちハットだのチルダなの細かい印を付けるのはメンドクセー -- と、そう感じたらしめたものです。全部 a という記号で表して、出現する文脈に応じてテケトーに解釈すればいいのです。
実際の計算では、対象/射への関手/自然変換の適用が出てきます。DOTNでは適用にドット記号を使い、しかも左から右に書きます。a.F、f.F、a.α, f.α とかですね(f.α については「自然変換の計算法 DOTN二号」の追記を参照)。この適用「.」は、「細かい印はメンドクセー」の精神で格上げ同一視を行うと、横結合(スター結合、グッドモン結合)「*」に置き換えて差し支えありません。a*F、f*F、a*α, f*α です。
結局、最上位=自然変換まで格上げされると、必要な計算は縦結合「;」と横結合「*」だけです。縦結合と横結合の組み合わせのバラエティは膨大になることがあり、それが複雑さにつながっています。しかし、この組み合わせのあいだの同値性は、エレベーター規則(交替律)で統制されています。エレベーター配置の同値性は、絵の目視で比較的容易に判断できます -- それが絵算の大きなメリットです。