米田の補題をストリング図で描いておくと、米田同型〈the Yoneda isomorphism〉の作り方を忘れないんじゃないかと思います。$`%
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\id}{\mathrm{id} }
\newcommand{\mrm}[1]{\mathrm{#1} }
\newcommand{\In}{\text{ in } }
\newcommand{\Iff}{\Leftrightarrow }
\newcommand{\twoto}{\Rightarrow }
\newcommand{\whitestar}{ \unicode{x2606} }
\require{color}
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }%
\newcommand{\For}{\Keyword{For } }%
\newcommand{\Define}{\Keyword{Define } }%
%`$
内容:
米田の「y」記法
最近、スピヴァック〈David I. Spivak〉が $`y^A`$ のような記法を使っています。y は米田〈Yoneda〉からで、米田の「よ」記法と同じですが、手書きでもTeXでも容易に書けて視認性も良いのがメリットです。「米田テンソル計算 3: 米田の「よ」、米田の星、ディラックのブラケット 再論 // スピヴァックの指数記法」で詳しく紹介しましたが、もう一度手短に述べます。
まず、米田の「よ」記法から; 一般に、圏のホムセット $`\cat{C}(-, -)`$ を二項関手〈双関手〉とみなして、米田の「よ」記法は次のように定義します。
$`\For \cat{C} \in |{\bf CAT}|\\
\For A, B\in |\cat{C}|\\
\Define よ_A := \cat{C}(A, -) \;: \cat{C} \to {\bf Set} \In {\bf CAT}\\
\Define よ^B := \cat{C}(-, B) \;: \cat{C} \to {\bf Set} \In {\bf CAT}
`$
スピヴァックの米田の「y」記法では、ホムセットを $`z^x = \cat{C}(x, z)`$ のような累乗記法で書いて、どちらかの変数を固定します。
$`\For \cat{C} \in |{\bf CAT}|\\
\For A, B\in |\cat{C}|\\
\Define y^A := \cat{C}(A, -) \;: \cat{C} \to {\bf Set} \In {\bf CAT}\\
\Define B^y := \cat{C}(-, B) \;: \cat{C} \to {\bf Set} \In {\bf CAT}
`$
$`y^A, B^y`$ なら、上付き下付きどっちだっけ?と悩むことがありません。この記事では $`y^A`$ 記法を使います。
米田の補題
米田の補題については、次の記事で書いています。
上記過去記事では:
何の工夫もなしに、愚直な直接計算を使うことにします。
...[snip]...
圏論の最重要定理である米田の補題も、ご覧の通りの愚直な計算です。
と、図は一切描かずにひたすら計算だけしています。計算過程のなかに、次の米田同型の作り方が組み込まれています。
$`\quad \mrm{Nat}(y^A, F) \cong F(A) \In {\bf Set}`$
米田同型のテキスト表示は忘れがちので、視覚的な印象もあったほうがいいでしょう。ストリング図を描くことにします。ストリング図は、大きな圏も含む2-圏 $`{\bf CAT}`$ 内の図です。視覚的なセルは次の意味があります。
- 背景領域は圏(0-射)
- ワイヤーは関手(1-射)
- ノードは自然変換(2-射)
描画方向は、自然変換の縦結合の方向が上から下、関手の結合/自然変換の横結合の方向が左から右とします。
射とホムセット要素
ここから先で使うお絵描き〈picturing〉の技法に関しては次の記事を参照してください。
例えば、格上げ〈promote | bump up〉については、「圏論の随伴をちゃんと抑えよう: お絵描き完全解説 // 対象と射の格上げ」に説明があります。
$`\cat{C}`$ は圏とします。圏の射 と、その射をホムセットの要素とみたものを区別します。
- 圏の射は $`f:A \to X\In \cat{C}`$ と書く。
- 対応するホムセット要素を $`\hat{f}\in \cat{C}(X, A)`$ と書く。
圏の射 $`f`$ は、格上げして、
$`\quad f^\sim :: A^\sim \twoto X^\sim : \whitestar \to \cat{C} \In {\bf CAT}`$
として描きます。$`\whitestar`$ は単一の対象と恒等射だけからなる自明圏です。描画のときは、$`f`$ と $`f^\sim`$ は同一視します($`f^\sim`$ をあたかも $`f`$ であるかのように扱う)。
集合圏の終対象 $`{\bf 1}`$ や終対象からの写像も格上げするので、集合の要素 $`a\in A`$ は次の自然変換となります。
$`\quad a :: {\bf 1} \twoto A : \whitestar \to {\bf Set} \In {\bf CAT}`$
関手とみなした終対象 $`{\bf 1}`$ は点線で、自然変換とみなした要素は点線に繋がるノードで図示します。特に、三角形のなかに $`f`$ とラベルしたノードは $`\hat{f}`$ の意味です。
今説明した描画法で描くとして、次が成立します。なお、集合圏を表す背景領域は斜線で網掛けしました。
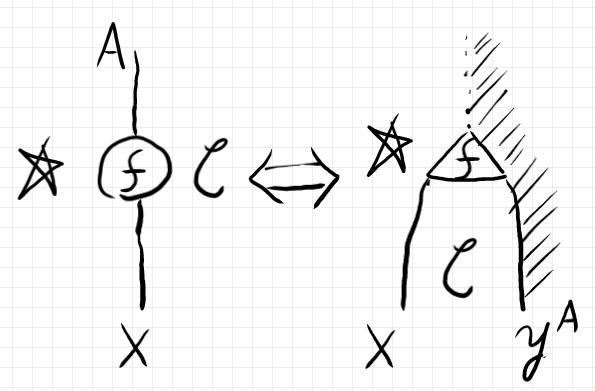
この事実をテキストで書けば:
$`\quad f:A \to X \In \cat{C} \Iff \hat{f} \in \cat{C}(A, X) \In {\bf Set}`$
$`y^A`$ の定義を思い出せば、次のようになることに注意してください。アスタリスクは関手の結合と自然変換の横結合の図式順演算子記号です。
$`\quad X * y^A \\
= X^\sim * y^A \\
= (y^A)(X)\\
= X^A\\
= \cat{C}(A, X)
`$
1:1 に対応する左右のストリング図を忠実にテキストに写しとれば:
- $`f^\sim :: A^\sim \twoto B^\sim : \whitestar \to \cat{C} \In {\bf CAT}`$
- $`\hat{f} :: {\bf 1}^\sim \twoto X^\sim * y^A : \whitestar \to \cat{C} \In {\bf CAT} `$
米田同型
米田同型を $`\mrm{Nat}(y^A, F) \cong F(A)`$ と書いたとき、左から右への写像(米田写像)をフラット記号、右から左への写像(反米田写像)をシャープ記号で表すことにします*1。
$`\quad (-)^\flat : \mrm{Nat}(y^A, F) \to F(A) \In {\bf Set}\\
\quad (-)^\sharp : F(A) \to \mrm{Nat}(y^A, F) \In {\bf Set}
`$
音の高さを抽象度とすると、“抽象的な自然変換”を“具体的な集合の要素”にエンコードして抽象度を下げるのでフラットです。逆方向は、“具体的な集合の要素”を“抽象的な自然変換”にデコードして抽象度を上げるのでシャープです。
フラット写像 $`(-)^\flat`$ による対応 $`\alpha \mapsto \alpha^\flat`$ を図示すると次のようになります。
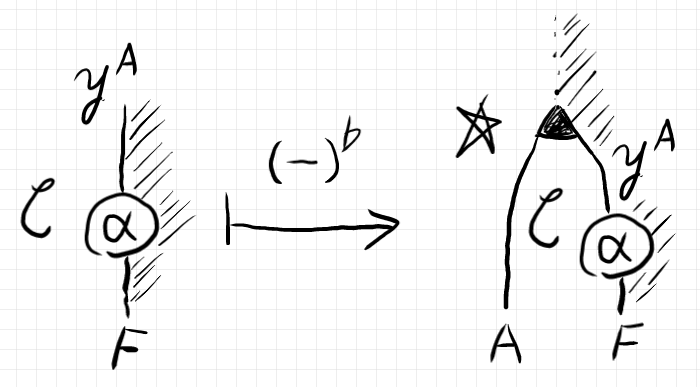
ここで、小さな黒い三角 $`\blacktriangle`$ の意味は次のとおりです。
$`\quad \blacktriangle \\
= \blacktriangle_A \\
= \widehat{\id_A}
`$
恒等射のホムセット要素が黒三角ですね。絵に忠実なテキスト表現ならば:
$`\quad \blacktriangle_A :: {\bf 1}^\sim \twoto A^\sim * y^A : \whitestar \to {\bf Set} \In {\bf CAT}`$
次に、要素 $`z\in F(A)`$ を選んだとき、自然変換成分 $`{z^\sharp}_X`$ による対応
$`\quad \cat{C}(A, X) \ni f \mapsto {z^\sharp}_X(f) \in F(X)`$
を図示すると次のようです。([追記]絵が間違っていたので差し替えました。[/追記])
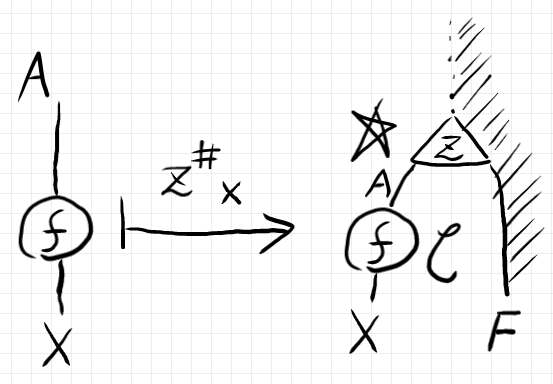
これも $`{\bf CAT}`$ に格上げ〈promote | bump up〉した図で、次の意味です。
$`\quad ({z^\sharp}_X(f))^\sim = z^\sim ; (f^\sim * F)\; :: {\bf 1}^\sim \twoto X^\sim * F : \whitestar \to {\bf Set} \In {\bf CAT}`$
$`\cat{C}`$ や $`{\bf Set}`$ 内部で起きている現象も、すべて $`{\bf CAT}`$ に引っ張り出して観測します。集合の要素/集合/写像/圏の対象/圏の射/圏/関手/自然変換が、すべて同じキャンバスに描けることになります。
米田の補題の補題
米田の補題の主張は、フラット写像 $`(-)^\flat`$ とシャープ写像 $`(-)^\sharp`$ が互いに逆になることです。この主張を示す際に必要となる“補題”に次があります。
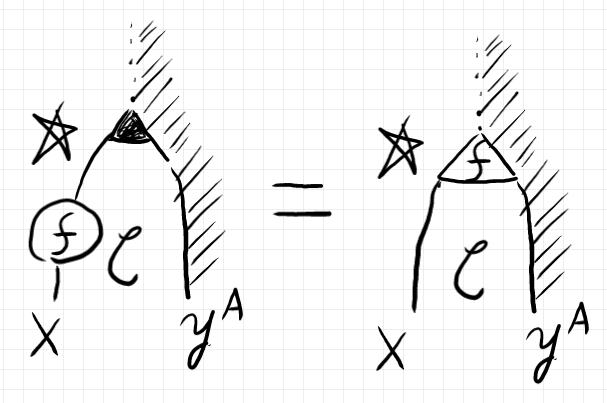
このストリング図等式を(必要があれば)テキストに書き下してみれば、比較的当たり前のことを言っていると分かるでしょう。
米田同型で $`\alpha \leftrightarrow a`$ と対応しているなら、次のストリング図等式が成立します。
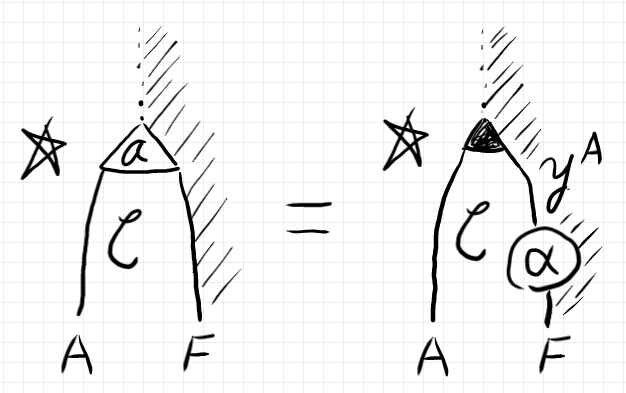
今回のこの記事では、ストリング図とテキスト表現の相互関係について詳しくは述べませんでしたが、機会があればもう少し丁寧な説明をするかも知れません(しないかも知れません)。
*1:音楽記号を使う記法はテンソル計算で使われています。ベクトル空間から双対空間に移る写像がフラット、その逆がシャープです。この場合の上げ下げは座標成分添字の上げ下げに合わせているようです。