ヴォエヴォドスキーやアウディ達がホモトピー・ラムダ計算/ホモトピー型理論*1を開発しています。
この新しい動きはここ数年のことです。実はもっとずっと以前から、計算科学とホモトピーの接点はありました。並列処理の解析にホモトピーを利用する、という話です。僕の知っている範囲で、そういうことをやっている代表的な人々は、Gaucher, Goubault, Grandis というGが付く名前の三人。つまり、G3。爺さんじゃないよ(爺さんはワシじゃ)。
また発音が気になって発音サイトで調べたのですが:
- Philippe Gaucher フィリップ・ゴシェー(フランス語)
- Eric Goubault エリク・?? (フランス語)
- Marco Grandis マルコ・グロンディ(イタリア語)
Goubaultの発音は不明でした。高山幸秀氏のページ http://www.ritsumei.ac.jp/se/~takayama/DIARY/Apr00b.html に「エコール・ノルマルの貴公子Eric Goubault」なんて書いてありますから、フランスの方ですね。
それはさておき、なんで並列処理とホモトピーが関係するのか大雑把に言うと(詳しくは分からない); 計算過程の進行とは状態空間における軌跡だと思えます。単純なケースを考えて、1つのプログラムの状態が1つの実数xで表されるとします。xは時間の関数となるので、x(t) (tは時間のパラメータ)と書けます。もう1つのプログラムがあって、それは y(t) で表現できるとしましょう。すると、2つのプログラムが一緒に走ったときの軌跡は (x(t), y(t)) なので平面曲線になります。
開始状態 P0 = (x0, y0) と終了状態 P1 = (x1, y1) を固定して、時間を0-1区間に正規化すると、プログラムの実行は、γ(t) = (x(t), y(t)) という曲線で表現され、γ(0) = P0、γ(1) = P1 となります。
プログラム実行の定量的なことは無視して、曲線(実行の軌跡)γとγ'が連続的に移りあえるなら同値としましょう。状態点P0から出発し、状態点P1に至る曲線をこの同値関係で分類した(割り算した)集合を考えると、これってホモトピーですよね。
平面内でホモトピーを考えても自明じゃないのか? と思うでしょ。そうでもないのです。2つのプログラムが共有資源へのアクセスを持つと、排他制御の関係から許されない状態が生まれます。この「許されない状態」を状態空間から抜き取ると(補集合を取ると)自明ではない位相になります。定番として引用される例は「スイス国旗」(Swiss flag)と呼ばれているものです。
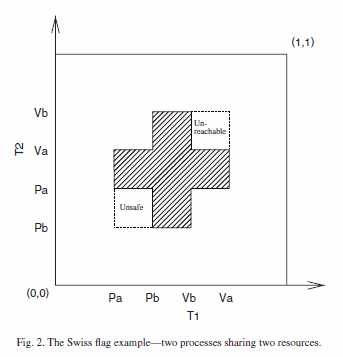
(この図は http://mook.inf.ed.ac.uk/twiki/pub/Sandbox/MarkGrantSandbox/Concurrency.pdf より)
平面(あるいは矩形)から十字架の形を抜き取った図形が状態空間です。普通のトポロジーだとこれは、平面から1点を取り去った図形と同じですが、Gさん達が使っている「並列処理のトポロジー」は、普通のトポロジーと少し違います。正確に言うと、トポロジーが違うというよりはホモトピーの定義が違うのです。実際の状態や時間には不可逆性があるので、状態空間に進行方向を考えた有向トポロジー(directed topology)を考え、ホモトピーもそれにあわせた有向ホモトピーを使います。
[追記 date="2011-04-22"]有向ホモトピーでは、亜群になることが保証されないので圏ですね。修正します。[/追記]
有向ホモトピーを定義するときは、基点付き空間 (X, p) のループを使う方法はうまくなくて、始点と終点をp, qとしたホモトピー集合 H(X, p, q) を考えます。p, q を動かして、Hom(p, q) := H(X, p, q) とすると、Hom(-, -) は圏のホムセットとなります。こうして有向トポロジー構造を持つ空間Xから作った圏が基本群ならぬ基本亜群圏(fundamental groupoidcategory)です。高次基本亜群圏を考えることができて、最終的には基本∞亜群圏(fundamental infinity-groupoidcategory)にまとめられます。
現実の状態空間を具体的に記述して、その基本亜群圏を計算するのはなかなか大変そうですから、並列処理システムの検証に有向ホモトピーを用いるのはチョト難しそうです(ものすごく難しいかな?)。でも、並列プログラムの実行が、エキゾチックな空間内を旅する軌跡で表現されるってこと自体が楽しいでしょ。