ホモトピー変形と自然変換

最近、ホモトピーに触れたエントリーを2つ書きました。

• ホモトピー・ナントカ
• ホモトピー同値は何故重要なんだろう

ホモトピー論と高次圏論は似ています。“似てる”とかのハナシではなくて、実際は同じものである可能性が高いですね。かつて「ホモトピー代数」という言葉がありましたが、広く使われることはなかったようです。もし、用語「ホモトピー代数」が復活するなら、それはホモトピー論と高次圏論が融合した分野を指すことになるでしょう。

圏論にホモトピーの概念が含まれている簡単で基本的な例があるので紹介します。

内容：

1. ホモトピー変形
2. 関手のホモトピー変形
3. 関手のホモトピー変形の実例
4. 自然変換

ホモトピー変形

「ホモトピー・ナントカ」からホモトピーの定義を引用します。

Topを位相空間と連続写像の圏として、[0, 1]は位相空間と考えた実数区間とします。f, g:X→Y in Top のとき、次のような H:[0, 1]×X→Y in Top を、fからgへのホモトピーと呼びます。

• 任意の x∈X に対して、H(0, x) = f(x)、H(1, x) = g(x)

fとgは、「空間Yのなかに埋め込まれた（もとの形状がXである）図形を表す」と考えましょう。区間[0, 1]は時間パラメータの変域だとします。すると、ホモトピーHは、Yのなかの図形fが時間に沿って図形gまで変形するさまを記述しているとみなせます。このイメージから、Hをホモトピー変形と呼びましょう。

具体例を挙げます； X = S¹ = 円周 として、円周上の点は弧長パラメータθ（0≦θ＜2π）で表すとします。Y = R² として、fとgを次のように定義します。

• f(θ) = (cos(θ), sin(θ))
• g(θ) = (0, 0)

H(t, θ) を、((1 - t)*cos(θ), (1 - t)*sin(θ)) とすれば、H(0, θ) = f(θ), H(1, θ) = g(θ) となります。このホモトピー変形Hは、平面内の単位円がシュルシュルと縮んで1点（原点）に潰れてしまう変形を記述しています。

関手のホモトピー変形

位相空間と連続写像の圏Topの代わりに、圏と関手の圏Catのなかでホモトピー変形を考えてみます。

まず、実数区間[0, 1]に相当する圏を探します。J = {0→1} という圏が[0, 1]の代わりに使えます。詳しく書くと：

• Obj(J) = |J| = {0, 1}
• Mor(J) = {id₀, id₁, j}
• dom(j) = 0, cod(j) = 0
• 射の結合（composition）は自明。

対象と恒等射を同一視して、Mor(J) もJと書くことにして、J = {0, 1, j} のように略記します。

FとGを C→D という関手だとします。ホモトピー変形の定義を圏と関手に引き写せば、Η:J×C→D in Cat であって、次の条件をみたすものがFからGへのホモトピー変形となります。

• Η(0, -) = F(-)、Η(1, -) = G(-)

「Η」はエイチに見えますが、ギリシャ文字イータ（エータ）の大文字です（小文字はη）。

関手のホモトピー変形の実例

関手のホモトピー変形Ηを具体的に見てみましょう。圏Cとして簡単な圏を選びます。Jの場合と同じような略記法で書くとして、C = {A, B, f} で、f:A→B とします。JもCも2個の対象と3本の射からなる圏なので、その直積 J×C は、4個の対象と9本の射からなる圏となります。次の図のようですね。対象と恒等射は同一視した単なる点なので注意して下さい。

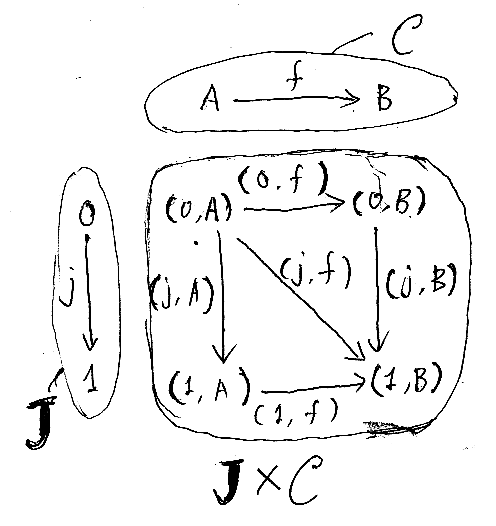
注目すべきは、(0, f);(j, B) = (j, A);(1, f) = (j, f) という可換性です。

関手 Η:J×C→D はJ×Cの4個の対象をDに移しますが、Η(0, -) = F(-)、Η(1, -) = G(-) という条件から：

1. Η(0, A) = F(A)
2. Η(0, B) = F(B)
3. Η(1, A) = G(A)
4. Η(1, B) = G(B)

つまり、FとGの値から行き先は完全に決まってしまいます。射に関しても：

1. Η(0, f) = F(f)
2. Η(1, f) = G(f)

残っていて決めなくてはならないのは、Η(j, B), Η(j, A), Η(j, f) の3本の射ですが、先ほどの可換性から Η(j, B), Η(j, A) が決まれば Η(j, f) は自動的に決まってしまいます。ここで、η_- := Η(j, -) と置きましょう。具体的には：

1. η_A := Η(j, A)
2. η_B := Η(j, B)

Η(j, -) の定義から：

1. η_A:F(A)→G(A) in D
2. η_B:F(B)→G(B) in D

結局、関手Η:J×C→Dを決めるとは、η_-:F(-)→G(-) in D を割り当てればいいことになります。

逆に、η_-:F(-)→G(-) in D というを割り当が可換性の条件を満たせば、関手Η:J×C→Dを与えます。

自然変換

はい、もうお分かりですね。ηは自然変換に他なりません。上記の例に限らず一般に、関手のホモトピー変形は自然変換のことだったのです。Jの代わりに、I = {0, 1, j, j^-1} を使うと可逆なホモトピー変形となり、これは関手の自然同値に対応します。関手のあいだの自然同値関係はホモトープ関係になり、圏同値は対象のあいだのホモトピー同値です。

以上のことは、類似性というより同じ定義とみなすべきでしょう。ホモトピー論と（高次の）圏論がどうやら同じらしいことの一番簡単な状況証拠です。