タイトルに「入門的ではない」と入れたのは;
先日の「関数型プログラミングとオブジェクト指向について、何か書く、かも」において、「型クラス入門」の記事を書くかもと予告じみたことを言ってしまったので、その入門じゃないぞ、と。でも、型クラスの話だぞ、と。そういう意味合いです。ヨロシク、アシカラズ。
型クラスの元祖はHaskellです。なので、「型クラス = Haskellの型クラス」という前提での解説が多いみたいです。しかし、元祖は“最初の試み”であるがゆえに、使用経験や後発の理論を活かすことが出来ず、むしろ問題をかかえていたりします。Haskellの型クラスも、なんだか残念なところが。
内容:
オーバーロードと人生
型クラス誕生の動機は、演算子オーバーロードと関係していました。そして、演算子オーバーロードをうまく扱う機能を期待されてもいるでしょう。実際、僕は演算子オーバーロードを欲しているので、その観点から型クラスを眺めることが多かったです。
でもね、オーバーロードと型クラスが分離不能に癒着しているわけではありません。理論的には独立に扱うことが可能です。オーバーロードに寄与しない型クラスもあるし、それはそれで有用だということです。
例えば、Standard MLのモジュールシステムのアイデアは型クラスと同様ですが、特にオーバーロードを意図してません。オブジェクト指向言語のインターフェイスは型クラス類似機能ですが、演算子のオーバーロードには直結しません。
オーバーロードは、名前・記号に対する実体をいつどのように結びつけるかに関わることなので、プログラミング・パラダイム、型システム/モジュールシステムとは一応切り離して議論できるはずです。
僕は、名前・記号が増えるのを非常に嫌っているので、個人的にはオーバーロードを希求してやまないのですが、皆んなにオーバーロードが必要とは限りません。Lisp由来の関数型言語は、あんまりオーバーロードしません。型システムがゆるいので、実質的に多相な関数を、実行時・型ディスパッチで書けるので「まーいいや」ってことでしょう。
強い型システムのもとでは、オーバーロード(非パラメトリックな多相)は難しくなります。OCamlでは、「-」が整数の引き算、「~-」が整数の符号反転、「-.」が浮動小数点数の引き算、「~-.」が浮動小数点数の符号反転です。印字関数も、print_char, print_string, print_int, print_floatなんて型ごとにタクサンあります。その分、確実な型推論という見返りがあるので、ユーザーに強い不満はないでしょう、たぶん。
というわけで、オーバーロードなしでも楽しい人生をおくっている人がいるので、オーバーロードを意図しない型クラスはあってもいいし、説明のときはむしろ、オーバーロードの話をいったん切り離したっていいでしょう。これは、僕がオーバーロードに拘り過ぎだった、という自戒の念から言ってます。
型クラスは何がうれしいのか(オーバーロードなしでも)
オーバーロード機能は無視するとして、それでもなお型クラスは有用なのだ、と言いました。では、型クラスは何を提供してくれるのでしょう? -- 「構造付き集合(structured set)としての型」概念を提供してくれます。構造とは、ブルバキによって提唱された“数学的構造”だと思ってください。ごく短く説明するなら、台集合(underlying set, carrier set)と、その上の演算、定数、関係を一緒に考えたものです。例えばモノイドは、台集合に二項演算と単位元(定数)を一緒に考えたものです((Haskellでは、モナドも型クラスとして定義されています: class Monad m where ... パラメータmは台集合じゃないぞ!? 確かにmは集合を表してはいません。ちょっと一般化して、集合とは限らない台対象(underlying/carrier object)の上に構造を載せたものとすれば辻褄はあいます。
例えばモナドは、関手を台対象(underlying/carrier object)とする構造なので、台の圏をSetから自己関手の圏End(C)に切り替えればいいのです。))。
圏論の観点から言えば、構造付き集合(structured set)は単に圏Cの対象です。ただし、圏Cは忠実関手 U:C→Set を持っているとします。この関手Uは忘却関手と呼ばれることが多いですが、構造的集合にその台集合を対応させる関手です。
上記の圏論的定義では余りにも味気ないので、構造の指標(signature)と(その指標に基づく)構造の公理(axioms)から具体的構造を定義します。モノイドの指標を擬似言語で宣言してみましょう(Coqで書いた指標と公理が「Coqの型クラスの使い方:バンドル方式とアンバンドル方式」にあります)。
signature MonSig := {
carrier M: Set;
operation mon_op: M, M -> M;
constant mon_unit: M;
};
これは記号の使い方を約束してるだけです。曰く:
- 台集合をMという名前(文字)で表す。
- M上の二項演算をmon_opという名前で表す。
- Mのとある要素をmon_unitという名前で表す。
モノイドの公理は次のようなものです。
- 結合律: ∀x,y,z:M. mon_op(mon_op(x, y), z) = mon_op(x, mon_op(y, z))
- 左単位律: ∀x:M. mon_op(mon_unit, x) = x
- 右単位律: ∀x:M. mon_op(x, mon_unit) = x
指標と公理を一緒にしたものを形式セオリー(formal theory)、または単にセオリー(theory)と呼びます。モノイドのセオリーも擬似言語で書いてみます(もちろん、CoqやIsabelleの構文でも書けます)。
theory MonTh := {
signature := MonSig;
axiom assoc: ∀x,y,z:M. mon_op(mon_op(x, y), z) = mon_op(x, mon_op(y, z));
axiom unit_l: ∀x:M. mon_op(mon_unit, x) = x;
axiom unit_r: ∀x:M. mon_op(x, mon_unit) = x;
};
セオリー内に指標をインライン展開して書くなら:
theory MonTh := {
carrier M: Set;
operation mon_op: M, M -> M;
constant mon_unit: M;
axiom assoc: ∀x,y,z:M. mon_op(mon_op(x, y), z) = mon_op(x, mon_op(y, z));
axiom unit_l: ∀x:M. mon_op(mon_unit, x) = x;
axiom unit_r: ∀x:M. mon_op(x, mon_unit) = x;
};
Haskellの型クラスとは指標のことで、台集合(carrier)の指定をパラメータの形にしたものです。CoqやIsabelleの型クラスは公理も書けるセオリーです。なお、Isabelleで実際に「セオリー」と呼んでいるのは割と大粒度のモジュールのことで、ここで言ったセオリーじゃありません。
指標もセオリーも、お約束事と条件を記述した構文的存在物(つまり、書き物)に過ぎません。実際の構造的集合としてのモノイドは、指標の名前Mに実際の集合を割当て、mon_op, mon_unitにも実際の写像/要素を割当てたもので、公理をほんとに満たすものです。そういう構造的実体をモノイドと呼ぶのです。
型クラスの実際
Standard MLでは指標を素直にsignatureと呼び、型クラスという言葉は使いません。CoqやIsabelleの型クラスはセオリーのことです。指標は、公理をひとつも持たないセオリーで代用できるので、CoqやIsabelleに指標という概念はありません。そして、Haskellの型クラスは単なる指標のことでした。
指標、セオリー、型クラスの区別には神経質にならずに、ほぼ同義語として使います。公理を書けない言語が多い(つうか、普通のプログラミング言語は公理を書けない)ので、以下では公理は出しません。公理(型クラスの法則)はプログラマ/ユーザーの心のなかにある、でヨシとしましょう。
以下はそれぞれ、Coq, Standard ML, Haskellにおける、「モノイドを定義する型クラス」です。型インスタンス、つまり実際のモノイドも1個定義しています。
Class Mon := { m: Set; mon_op: m -> m -> m; mon_unit: m }. Require Import ZArith. Open Scope Z_scope. Instance IntMulMon : Mon := { m := Z; mon_op := fun x=>fun y=> x*y; mon_unit := 1 }.
signature Mon = sig type m val mon_op : m -> m -> m val mon_unit : m end structure IntMulMon : Mon = struct type m = int val mon_op = fn x=> fn y=> x*y val mon_unit = 1 end
class Mon m where mon_op :: m -> m -> m mon_unit :: m instance Mon Int where mon_op = (*) mon_unit = 1
言語ごとのネーミングコンベンションは無視して、名前は揃えてあります。でも、整数型を表す名前は、Z, int, Int とバラバラです。
上記の例では、整数値の集合(Z, int, Int)の上にモノイド構造を載せて実際のモノイド(型クラスMonのインスタンス)を作っています。二項演算は掛け算、単位元は1です。ところで、整数値の集合上には足し算もあり、これもモノイドになります。
Instance IntAddMon : Mon := { m := Z; mon_op := fun x=>fun y=> x + y; mon_unit := 0 }.
structure IntAddMon : Mon = struct type m = int val mon_op = fn x=> fn y=> x + y val mon_unit = 0 end
簡単ですね。あれ、Haskellでは? … 出来ません*1。
記号の乱用の実装法
Haskellの場合、演算子記号・関数名のオーバーロードだけではなくて、型名のオーバーロードも許しています。この型名のオーバーロードはとてつもなく便利ですが、弊害もあります。後知恵で言えば、「悪いお薬」だったと思います。服用するとモノ凄く元気になるが、長期的には心身を蝕んでしまうお薬だったと。
かつて、次のような記事を書いたことがあります。
これは、人間がモノイドMについて、「M = (M, m, e) とする」のような言い方を平気でするイイカゲンさを、コンピュータにも実装すべきかも、という内容です。Haskellは、この便利なイイカゲンさを実装しているのです。
M = (M, m, e) のイイカゲンさを解決する解釈は二通りあります。
- M = (Carrier(M), mM, eM)
- Enhance(M) = (M, mM, eM)
一番目の解釈: Mはモノイド構造に付けられた名前で、右辺のM(正確には Carrier(M))はモノイドMの台集合を表している。
二番目の解釈: Mは集合の名前で、左辺のM(正確には Enhance(M))は、集合Mに対して演算と単位を付与して作ったモノイドを表している。
CoqもStandard MLも、一番目の乱用はサポートしています。特にCoqは、組み込みでCarrier相当の機能(implicit coercion)を持っています。
我々人間にとってより自然で便利なのは、たぶん二番目の解釈です。そしてHaskellは、二番目の解釈を実装しています。Int = (Int, (*), 1) の解釈は、Enhance(Int) = (Int, (*), 1) なのです。Enhanceに相当する対応 Int |→ (Int, (*), 1) がinstance宣言で登録されます。
本来は単なる集合の名前であったIntを、文脈により様々な構造として再解釈を許すのですからこれは便利です。ごく一部を以下に図示します。左側の「集合としての型」を、右側の「構造としての型」としても流用できるのです。
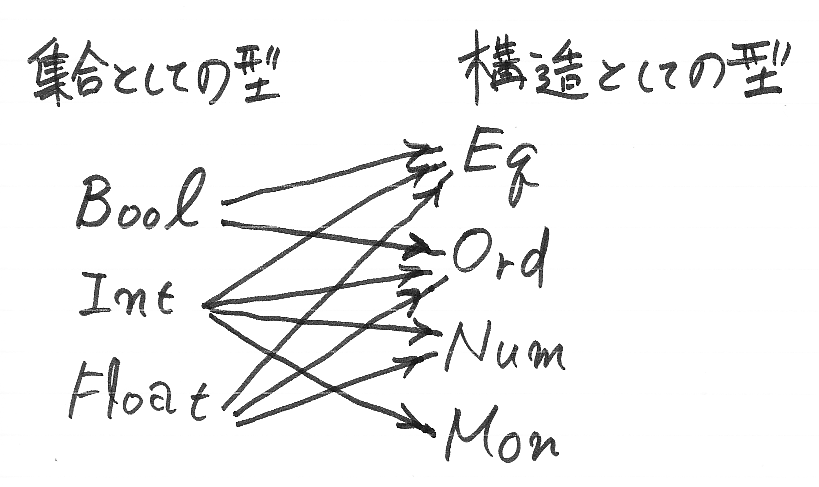
Haskellの型クラスは何がマズイのか
Haskellでは、モノイド自体に名前を付けることが出来ません。CoqやStandard MLにおけるIntMulMonのような名前はないのです。集合としての型であるIntを経由して、Intの標準モノイド構造 Mon Int としてのみ構造にアクセスできます。このことが記号の乱用をうまく扱える根拠になっています。しかし、Int(整数の集合)上のモノイド構造は無数にあるわけで、「台集合ひとつにモノイドもひとつ」という制限は、用途によっては耐え難いものとなります。
またHaskellでは、マルチパラメータ・クラスは色々と細工をしないと実現できません。よく引き合いに出される、要素の型がeであるコレクション型ceの型クラスは:
-- このままではうまくいかない class Collects e ce where empty :: ce insert :: e -> ce -> ce member :: e -> ce -> Bool
Coqでは、特に問題もなく書けます*2。構造に対する台集合が2つあり、それらをパラメータにしています。
Class Collects (e: Type) (ce: Type) := { empty : ce; insert : e -> ce -> ce; member : e -> ce -> bool }. Require Import List. Instance IntListColl : Collects Z (list Z) := { empty := nil; insert := fun x=> fun xs=> x::xs; member := fun x=> fun xs=> existsb (fun y=> x =? y) xs }.
コレクションの実装にはリストを使うことに決めて、要素の型をパラメータとする場合をStandard MLで書いてみます*3。
signature Eq = sig type t val eq : t -> t -> bool end signature Collects = sig type ce type e val empty : ce val insert : e -> ce -> ce val member : e -> ce -> bool end functor ListColl(X: Eq) : Collects = struct type ce = X.t list type e = X.t val empty = [] val insert = fn x=> fn xs=> x::xs val member = fn x=> fn xs=> exists (fn y=> X.eq x y) xs end (* 型インスタンスの生成 *) structure EqInt : Eq = struct type t = int val eq = fn x=> fn y=> x = y end structure IntListColl : Collects = ListColl(EqInt)
Haskellが実装した記号の乱用はやはり「乱用」だったのです。特定の状況ではうまく動くものの、より複雑な状況/広い範囲に対しては破綻します。綻びを修復する試みはされていますが、不必要な複雑さを導入しているように思えます。
利便性のためには確かに「乱用=オーバーロード」が必要です。しかし、オーバーロードは、どうやっても恣意性/無法則性を免れません。それを基本メカニズムに採用すれば、恣意性/無法則性をシステムに招き入れることになります。オーバーロード機能は、ユーザーの好みにより利用する/しないを制御できるオマケ便利機能にすべきだと思います。
…
…
そんなオーバーロードを実現したいだけの人生だった。