名前や記号の多義的使用をオーバーロードと呼びます。オーバーロードとは「曖昧な表現を使う」ことだ、と言ってもいいでしょう。曖昧さを嫌うコンピュータに、曖昧な表現を理解させるのは難しいことです。コンピュータに関する技術や理論以前に、「我々人間は、曖昧な表現をどう使い/どう解決しているのか?」と問う必要があります。
内容:
- Haskellの場合 -- The・構造の仮定
- 要素とコレクションの事例
- 型クラスの境界線は引けるのか
- 名前・記号の問題は難しい
Haskellの場合 -- The・構造の仮定
「入門的ではない型クラスの話:Haskellの型クラスがぁ (´^`;)」において:
後知恵で言えば、[注:Haskellのオーバーロード・メカニズムは]「悪いお薬」だったと思います。服用するとモノ凄く元気になるが、長期的には心身を蝕んでしまうお薬だったと。
Haskellが実装した記号の乱用はやはり「乱用」だったのです。特定の状況ではうまく動くものの、より複雑な状況/広い範囲に対しては破綻します。綻びを修復する試みはされていますが、不必要な複雑さを導入しているように思えます。
なんて言いました。Haskellファンはムッとしたかも知れません。
そもそも型クラスはHaskell起源だし、モジュラー化とオーバーロードの手法として大成功を収めたのは確かです。その点は高く評価するのは言うまでもありません。しかし、何ゆえに成功したのか? と考えてみると、特定の(かなり狭い)状況でしか成立しない原理に強く依拠している、と思えるのです。この原理について説明し、さらに、この原理に一般性・汎用性がないことを例示します。
Haskellの型クラスは、演算子記号・関数名のオーバーロードだけでなく型名のオーバーロードも可能とします。そして、型名をオーバーロードすることが必須です。その様子は「入門的ではない型クラスの話:Haskellの型クラスがぁ (´^`;)」に絵で示しました。
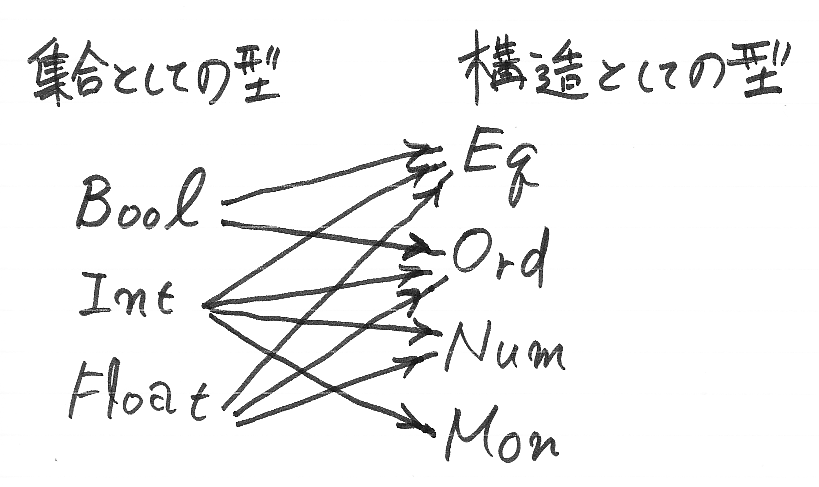
例えばIntという型名が、「EqのインスタンスとしてのInt/OrdのインスタンスとしてのInt/NumのインスタンスとしてのInt」と多様な解釈を持ちます。この多様な解釈を可能としている前提は次のものです。
- 集合(としての型)が決まれば、その上の構造(演算、特定要素、関係など)はひとつだけ決まる。
例えば、「整数の等値性」と言えば、誰でも同じイコールを思い浮かべます。「整数の順序関係」といえば「あの大小関係」で間違いないでしょう。つまり、型Intに対して「The・等値性」「The・順序関係」が決まるので、Eq Int, Ord Int などと書けて、それを曖昧性なく解釈できます。
ところが、「整数の二項演算」となると、「構造(演算、特定要素、関係など)はひとつだけ決まる」という原理があやしくなります。整数に対して「The・二項演算」は一意に決められないからです。
二項演算で既にあやしいとなると、より複雑な構造に対して、与えられた集合上の「The・構造」が決まるのでしょうか? 普通に考えれば、まー無理ですよね。
要素とコレクションの事例
次のコードは、「入門的ではない型クラスの話:Haskellの型クラスがぁ (´^`;)」のサンプルの再掲ですが、一筋縄ではいかない「コレクションを表す型クラス」です。
class Collects e ce where empty :: ce insert :: e -> ce -> ce member :: e -> ce -> Bool
Collects e ce において、eは要素の型で、ceはコレクション(要素の集まり)の型です。型eと型ceが決まれば、その上のコレクション構造が決まるわけです。
それって、ほんとでしょうか? Collects Int Int とか Collects Int Bool とかを見て、「The・コレクション構造」をイメージできますか? 無理ですよね。2つの型を並べて、それをコレクション構造の名前として使用するのは現実離れしています。
想定される反論は以下のものです; 勝手な型e, ceに対してコレクション構造が決まるわけではない。eとceは無関係ではなく、どちらかを決めればもう一方も決まる。例えば、要素の型がInt、コレクションの型は[Int](Intのリスト)のように。
この反論を信じるなら、e→ce または ce→e の方向に「The・対応」があることになります。「Int型とIntのリスト型」なら「The・対応」があるでしょうが、典型例だけを見て一般化するのは危険です。
型クラスの境界線は引けるのか
Haskellでは、要素の型eとコレクションの型ceをパラメータにしていますが、一般的なコレクション構造のインターフェイスを記述する目的なら、パラメータである必然性はありません。Coqでパラメータを使わない形に書いてみます。[追記]Coqはシンタックスハイライトされない。悲しい。[/追記]
Class Collects := { e: Type; ce: Type; empty : ce; insert : e -> ce -> ce; member : e -> ce -> bool }.
ちなみにStandard MLでも同じように書けます。
signature Collects = sig type e type ce val empty : ce val insert : e -> ce -> ce val member : e -> ce -> bool end
まずは典型的な型インスタンスを定義しましょう。
(* インスタンスの実装に使うライブラリ *) Require Import Bool. Require Import ZArith. Open Scope Z_scope. Require Import List. Instance IntListColl : Collects := { e := Z; ce := list Z; empty := nil; insert := fun x=> fun xs=> x::xs; member := fun x=> fun xs=> existsb (fun y=> x =? y) xs }.
見慣れないかも知れないCoqの構文を表にして説明しておきます。↓
| Type | すべての型からなる“型の型” |
| Z | 整数型 |
| list | リスト型構築子 |
| fun | ラムダ抽象 |
| nil | 空リスト |
| :: | consの中置演算子 |
| existsb p xs | リストxsの要素で述語pを満たすものがあればtrue, なければfalse |
| =? | 整数(Z)のイコール(スコープ依存) |
次に、固定サイズの配列とか長さが有限のキューのように、格納限界があるコレクションを考えてみます。以下は3個までの要素を保存できるコレクションです。
Instance IntSize3Coll : Collects := { e := Z; ce := list Z; empty := nil; insert := fun x=> fun xs=> if leb (length xs) 2 then x::xs else xs; member := fun x=> fun xs=> existsb (fun y=> x =? y) xs }.
lebは自然数の不等号≦のことです。リストの長さが3以上(3にしかならないけど)だと、insertが黙って失敗します。
挿入すべき要素を黙って捨てるのはヒドイので、新しい要素はちゃんと保存して、代わりに古い要素を捨てることにしましょう。そして、格納限界を要素1個にします。
…… ん? それって、単に上書き更新する変数と同じことじゃん。
(* 上書き更新する整数変数のモデル *) Instance IntIntColl : Collects := { e := Z; ce := Z; (* 変数が保持する値 *) empty := 0; (* 初期値 *) insert := fun x=> fun y=> x; (* 上書き=破壊的代入 *) member := fun x=> fun y=> x =? y (* 現在値の検査 *) }.
同じようにして、「上書き更新する真偽値変数のモデル」BoolBoolCollも定義できます。次は、真偽値変数に整数を代入するモデルです。そのままでは代入できないので、0を偽、それ以外を真に変換して代入します。
(* 上書き更新する真偽値変数と 整数値を無理やり代入するモデル *) Instance IntBoolColl : Collects := { e := Z; ce := bool; (* 変数が保持する値 *) empty := false; (* 初期値 *) insert := fun x=> fun y=> negb (x =? 0); (* 整数を真偽値に直して代入 *) member := fun x=> fun y=> eqb y (negb (x =? 0)) (* 現在値の検査 *) }.
negbは真偽値の否定(NOT)、eqbは真偽値のイコールです。
ここまでで、「要素の型, コレクションの型」として、「Z, list Z」、「Z, list Z(長さ3まで)」、「Z, Z」、「bool, bool」(ソースコードは省略)、「Z, bool」の例を挙げました。「要素の型, コレクションの型」も多様だし、コレクション型の実装もまた多様です。どれかを決めたら残りは一意に決まるなんて事はありません。
次の反論がありそうです; 「Z, Z」(Haskellなら「Int, Int」)とか「Z, bool」(「Int, Bool」)とか変なモノはコレクションとは呼ばない。コレクションの実例(型インスタンス)をもっと制限すれば関連性は一意に決まる。
では、どんな実装(型インスタンス)なら「コレクション」と呼んでいいのでしょうか? 境界線を確定できるでしょうか。構造の指標を定義しても、公理を書けないHaskellでは(ほとんどのプログラミング言語では)フォーマルに「コレクション」を規定するのは無理です。結局は人間同士の合意であり、その合意された暗黙のセマンティクスを、型クラス名、型名、関数名などの名前に込めているのです。
名前に込めた思いを理解しないコンピュータは、次の型クラス定義だって、まったく同じ扱いをします。「要素(element)」「コレクション(collection)」という言葉から、勝手に色々と連想するのは人間だけです。
Class CC := { ss: Type; tt: Type; cc : tt; ff1 : ss -> tt -> tt; ff2 : ss -> tt -> bool }.
[追記]オマケ: コレクションの性質を公理にするなら、例えば次のようかな。∀と¬は論理記号の全称と否定。
- ∀x:e. ¬(member x empty) (emptyは要素をまったく含まない)
- ∀x:e.∀y:ce. (member x (insert x y)) (挿入した要素は入っている)
この公理だと、満杯になるとinsertが何もしない有界バッファは失格。上書き変数のモデルはOK。←いや、ダメだ。初期値が入るから公理1が満たされない。コレクションの型をオプション型(Maybe型)にして初期値は未定義にすればいいかな。[/追記]
名前・記号の問題は難しい
「名前に込めた思い」の「思い」は、「一人の思い」ではなくて、複数の人々で共有された思い、別言すれば「共通認識、暗黙の合意、言語的習慣」などです。また、「その場の空気、話の流れ」などもコミュニケーションの前提として共有されるものでしょう。多義語/乱用された記号の意味は、共有された思いにより解決されます。しかも、その解決法さえも暗黙に共有された知恵によります。
Haskellの型クラスの場合は、「集合(基本的な型)の名前を、構造(より複雑な型)の名前に流用する」という知恵を曖昧性解決原理に採用したのです。実際、この知恵(記号の乱用法)は人間同士で広く使われていて、記号・名前の節約に絶大な効果を発揮します。
しかし、記号の乱用をやり過ぎると混乱するので、明示的な記法に切り替えたり、文脈を固定してから略記を使うなどの方法が併用されます。我々は、無意識にけっこう色々うまくやっています。単一の原理に頼っているわけではありません。
人間が膨大な名前を正確に憶えて使い分けられるなら、そもそもオーバーロードなんて不要なんです。オーバーロードは人間のための機能なので、我々が「曖昧な表現」にどう対処しているかを定式化する必要があります。コンピュータだけでなく、人間の理解・認識に関わるので、どうしたって話は難しくなりますね。