圏論の随伴をちゃんと抑えよう - 檜山正幸のキマイラ飼育記 (はてなBlog)

[追記 date="後日"]日本語の表記として「抑える」より「押さえる」が正しい気がしてきたけど、このままにします。使い分けがさほど明確なわけじゃないし、「抑える」に「支配下に置く」ような雰囲気もあるので。[/追記]

「テキスト記法を図式順で書くか反図式順で書くか？」「ストリング図の上下左右方向をどうするか？」などの過剰なバラエティ（あるいは混乱）が、圏論の学習を困難にしている要因のひとつだろう、という話は何度も何度も何度も書きました。最近の記事を2つだけ挙げれば：

上下左右をきちんと区別しないと話がワヤクチャになる典型的な例に、随伴〈adjoint, adjunction〉の定義があります。僕も「どっちが右だっけ？」「域だっけ、余域だっけ？」「εって、単位？それとも余単位？」とか、ねんじゅう迷っています。

標準的な表記法（書き方の約束）や描画法（描き方の約束）はないので、自分で記法／図法を決めた上で、定義の内実を納得するしかありません。上下左右に惑わされずにちゃんと納得しましょう。

[追記]続編である「圏論の随伴をちゃんと抑えよう：お絵描き完全解説」を書きました。目次に続編の内容も含めます。[/追記]

内容：

随伴系の書き方と事例
左と右を忘れるんだが
ホムセット同型方式の定義
単位と余単位
転置と反転置
ニョロニョロ方式の定義
ニョロニョロ方式のメリット
随伴系の書き方を約束する

お絵描き完全解説の内容：

圏の圏における絵算
対象と射の格上げ
図式順記法と混合記法
絵算で何をやるのか
転置オペレータ／反転置オペレータとその描画
転置と反転置の自然性
ホムセット同型からニョロニョロへ
絵算のススメ

圏論における随伴

もともと、デカルト圏に関する記事を書き始めたんですよ。そのなかで随伴概念を使うので、準備として随伴の話をしだしたら長くなったので独立させたのがこの記事です。

圏論の随伴って、とても重要な概念ですが、その割には用語法も表記法も曖昧だし、定義自体もけっこうイイカゲンに語られてますね。

「随伴」という言葉で一括りにされている概念を腑分けして、その構成要素を取り出してみます。

随伴対〈adjoint pair | 随伴ペア〉：随伴の構成要素で、2つの圏C, Dのあいだを逆方向に結ぶ関手の対。丁寧に言えば、互いに随伴な関手の対、関手の随伴対〈adjoint pair of functors〉。
左随伴（関手）〈left adjoint (functor)〉：関手の随伴対のなかの一方。
右随伴（関手）〈right adjoint (functor)〉：関手の随伴対のなかのもう一方。
単位〈unit〉：随伴の構成要素となる自然変換。
余単位〈counit〉：随伴の構成要素となるもうひとつの自然変換。

随伴対は2つの関手の組ですが、どちらを左（あるいは右）と呼ぶかは、マックレーンの教科書（The Book）が出るまでは人によりバラバラだったようです。随伴対は、単に“逆方向の関手の組”というだけではなくて、2つの関手は単位／余単位という自然変換で関係づけられています。さらには、単位／余単位を特徴づける等式（ニョロニョロ関係式〈snake {relation | equation | identity}〉）があります*1。

こういった随伴概念を構成する構造全体を、ここでは随伴系〈adjoint system〉と呼ぶことにします。随伴系は、2つの圏、2つの関手、2つの自然変換、2つの法則（自然変換の等式）で構成されます。

圏： C
圏： D
関手（対の左）： F:D→C
関手（対の右）： U:C→D
自然変換（単位）： η::D^⇒F*U:D→D
自然変換（余単位）： ε::U*F⇒C^:C→C
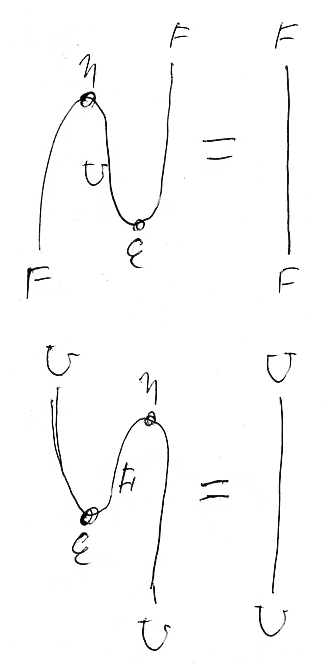
等式（ニョロニョロその1）： (η*F);(F*ε) = F^
等式（ニョロニョロその2）： (U*η);(ε*U) = U^

記法は図式順〈diagrammatic order notation〉（ココを参照）で、恒等〈identity〉を表すためにハット〈キャレット | サーカムフレックス〉記号'^'を使っています -- A^ = id_A、 C^ = Id_C、 F^ = ι_F（恒等自然変換）。

随伴系を構成する素材を律儀に書くなら、(C, D, F, U, η, ε)となります。関手の対(F, U)で全体を代表させるのは略記です。このテの略記はよく使われます。例えば、集合M、要素e、二項演算m:M×M→M で構成され、結合律、左単位律、右単位律を満たす構造がモノイドですが、(M, e, m)の代わりに単にMと略記します。

名詞"adjunction"と形容詞（名詞的に使うこともある）"adjoint"の訳語はどちらも「随伴」だと思いますが、adjunctionとadjointを区別することもあります。adjunctionは、2-圏の文脈で定義される一般的な構造を意味することがあります（次のnLabエントリーを参照）。

https://ncatlab.org/nlab/show/adjunction

具体的な2-圏Cat（または大きな圏も許すCAT）におけるadjunctionの例が、関手の随伴対〈随伴ペア〉です。adjunctionの別な例として、ベクトル空間の双対〈双対空間ペア〉があります。「随伴ペア」と「双対ペア」のあいだに明確な境界線が引けないのは、どちらもadjunctionの具体例で同じ構造を持つからです。そのことは例えば次の記事で書いています。

用語の使用状況をまとめておきましょう。

随伴対〈随伴ペア〉と言った場合、その対を含む随伴系を意味している。
対〈ペア〉の片方を左、もう一方を右と呼ぶ（後で詳述）。
単に「随伴」と言った場合、随伴系のことか、随伴対の一方（左随伴または右随伴）のことだろう。
圏、関手、自然変換から構成される具体的な随伴系と、2-圏により抽象化した随伴系〈adjunction〉がある。
この記事で転置（後述）と呼ぶ関係を随伴〈adjunct〉と呼ぶこともある。
モノイド圏における随伴概念は双対概念である。随伴と双対の区別は曖昧。

一般論として2-圏における随伴系〈adjunction〉があり、Cat（またはCAT）における随伴系は「関手の随伴対」と略称され、単対象2-圏とみなしたモノイド圏における随伴系は「双対」と呼ばれる、と理解するのがよいでしょう。

随伴系の書き方と事例

[追記]更新された随伴系の書き方は「随伴に関する注意事項」参照。[/追記]

前節で述べたように、関手の随伴系〈adjoint system〉の構成要素を並べれば、(C, D, F, U, η, ε)です。このなかのF, Uを取り出して全体を代表させます。しかし、随伴対の主役はF, Uではなくて、η, εのほうです。F, Uはηとεを載せる台（underlying things）として在るだけです。

もっとも、主役より台のほうを取り出して略記に使う習慣は一般的ではあります。先ほどの例、モノイド(M, e, m)において、モノイド構造の主役は二項演算 m:M×M→M でしょう。法則（単位律、結合律）も二項演算に関する法則です。しかし、台集合Mを表に出して「モノイドM」という言い方をします。下部構造（台）で上部構造を暗示する呼び方は、何に注目すべきかをミスリードしているので不適切だと思いますが、習慣なんで如何ともしがたい。

F, Uが関手の随伴対であるとき、単なる(F, U)ではなくて、F -| U という書き方をします。記号'-|'の存在により「これは随伴対だぞ」と指示するわけです。この記号'-|'を見たら、背後に単位／余単位であるη／εの存在と、ニョロニョロ関係式が暗黙に仮定されるのです。単位／余単位とニョロニョロ関係式を絵（ストリング図）で描けば次のようです。（[追記]「お絵描き完全解説」参照。[/追記]）

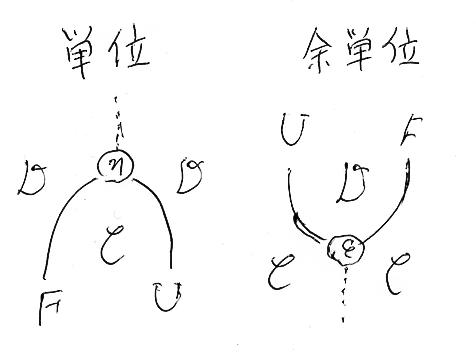
ところで、関手の随伴対 F -| U というと、単位／余単位より、次のようなホムセットの同型を想定する人が多いでしょう。

C(F(A), X) $\stackrel{\sim}{=}$ D(A, U(X))

この同型を与える写像をΦと書くことにします。

Φ:C(F(A), X)→D(A, U(X))

同型写像Φを中心に据えた随伴系の定義を、仮にホムセット同型方式の定義と呼ぶことにします。それに対して、単位／余単位のニョロニョロ関係式を使うほうをニョロニョロ方式の定義と呼ぶことにします。これら二種類の定義の相互関係も随伴系の重要な話題です。

ここで、随伴系の具体例をひとつ挙げておきます。それは、ベクトル空間の自由生成と忘却関手（台集合関手）です。僕はいつも、この例を思い出したり、この例で確認したりします。

一般的な随伴系の構成要素(C, D, F, U, η, ε)を、次のように具体化します。

C = Vect = (適当なスカラー体の上のベクトル空間と線形写像の圏)
D = Set = 集合圏
(F:D→C) = (F:Set→Vect) = 自由ベクトル空間を生成する関手
(U:C→D) = (U:Vect→Set) = 忘却関手
(η::D^⇒F*U) = (η::Set^⇒F*U) = (生成系をベクトル空間の台集合に埋め込むこと)
(ε::U*F⇒C^) = (ε::U*F⇒Vect^) = (形式的線形結合を計算して実際の値を求めること)
(Φ:C(F(A), X)→D(A, U(X))) = (Φ:Vect(F(A), X)→Set(A, U(X))) = (線形写像の基底による表示)

随伴対として、F, GではなくてF, Uとしたのは、この具体例を連想しやすくするためです。FはFreeのF、UはUnderlyingのUです*2。

左と右を忘れるんだが

随伴対 F -| U はコンビとして意味を持ちます。片方を左随伴、もう一方を右随伴と呼びます。しかし、「左」「右」という形容詞は恣意的なものであり何の必然性もありません。「左」を「右」に言い換えてもまったく不都合はないのです。したがって、左右の区別をするヒントもありません。

コンビというと漫才を思い出します。漫才コンビでは、ボケとツッコミの役割分担があります。では、ボケ・ツッコミと立ち位置の左右に関係性はあるのでしょうか？「三四郎」は、ツッコミ小宮が左、ボケ相田が右です。「千鳥」は、ボケ大悟が左、ツッコミノブが右です。左右の立ち位置情報から役割を一般的に推定するのは不可能です。圏論の随伴対では、もっと対称性が高く、役割の区別も困難です。まー、「笑い飯」みたいなもんですね。（この段落の説明が随伴対の理解に寄与するかは不明。）

要するに、左右の区別は、どっちかを左と根拠なく決めたから、もう一方は右だとしか言いようがない、という事情です。F -| U と書いたときに左に出現するFを左随伴、右に出現するUを右随伴と呼びます。理由はありませんが、そう決めます。

随伴対 F -| U のホムセット同型を書いてみます。

Φ:D(F(A), X)→C(A, U(D))

このときも、Fが左、Uが右に出現します。とりあえず出現位置の左右で憶えてください。

随伴の単位ηを絵に描いたとき、絵が「左から右、上から下」方向で描いてあれば、Fのワイヤーが左、Uのワイヤーが右で辻褄があいます。ただし、描画方向が変われば左右も入れ替わります。

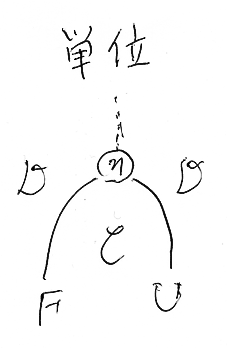
ホムセット同型方式の定義

ホムセットがハッキリと認識されているときは、ホムセット同型を使った随伴系の定義のほうが分かりやすいかも知れません。随伴系の全体は、(C, D, F, U, Φ)のように書かれます。

ホムセット同型方式の定義の場合は、写像Φが随伴構造の中核になります。このΦって何でしょうか？先ほど次のように書きました。

Φ:C(F(A), X)→D(A, U(X))

この書き方は不正確（略記）です。特定の対象A, X（A∈|D|, X∈|C|）に対してだけ同型写像が在るのではなくて、すべての対象のペア(A, X)に対して同型写像が付随しています。よって、対象のペアをインデックスにして次のように書くべきです。

Φ_A,X:C(F(A), X)→D(A, U(X))

Φは2つのインデックスを持つ写像の族です。しかも、単なる族ではなくて自然変換であることが要求されます。自然変換は2つの関手を結ぶものですが、Φの両端（域と余域）の自然変換はどんなものでしょう。

(A, X)|→C(F(A), X) という対応は、関手 F:D→C と関手 Id_C:C→C の直積 F×Id_C:D×C→C×C に、ホム二項関手 C(-, -):C^op×C→Set を繋げたものです。反変・共変の辻褄をあわせるために、全体は D^op×C→Set と考えます。同様に、(A, X)|→D(A, U(X)) も D^op×C→Set という関手となります。

したがって、自然変換Φのプロファイルは次の形になります。

Φ::C(F(-), -)⇒D(-, U(-)):D^op×C→Set

Φが自然同型（成分ごとに可逆な自然変換）であることは、(C, D, F, U, Φ)が随伴系を構成するための条件になっています。Φの自然性を表す次のような可換図式群が仮定されます。

f:A→B in D, X∈|C| に対して次が可換：

  C(F(B), X)-(Φ_B,X)→D(B, U(X))
    |                   |
  C(F(f), X)         D(f, U(X))
    ↓                  ↓
  C(F(A), X)-(Φ_A,X)→D(A, U(X))


g:X→Y in C, A∈|D| に対して次が可換：

  C(F(A), X)-(Φ_A,X)→D(A, U(X))
    |                   |
  C(F(A), g)         D(A, U(f))
    ↓                  ↓
  C(F(A), Y)-(Φ_B,X)→D(A, U(Y))

先の具体例「自由ベクトル空間の生成関手と忘却関手」では次のようです。

集合のあいだの写像 f:A→B とベクトル空間Xに対して次が可換：

  Vect(F(B), X)-(Φ_B,X)→Set(B, U(X))
    |                      |
  Vect(F(f), X)         Set(f, U(X))
    ↓                     ↓
  Vect(F(A), X)-(Φ_A,X)→Set(A, U(X))


線形写像 g:X→Y と集合Aに対して次が可換：

  Vect(F(A), X)-(Φ_A,X)→Set(A, U(X))
    |                      |
  Vect(F(A), g)         Set(A, U(g))
    ↓                     ↓
  Vect(F(A), Y)-(Φ_A,Y)→Set(A, U(Y))

これらの自然性の条件は、見落としてしまったり、直接使うのが煩雑だったりします。そこで、別な定式化であるニョロニョロ方式が登場します。

単位と余単位

ニョロニョロ関係式は、単位／余単位に関する法則です。ホムセット同型Φから、単位／余単位を構成しましょう。単位を η::D^⇒F*U、余単位を ε::U*F⇒C^ とします。それぞれを成分表示すれば：

η_A:A→(F*U)(A) in D
ε_X:(U*F)(X)→X in C

'*'は図式順の関手結合なので、反図式順で書けば：

η_A:A→UF(A) in D
ε_X:FU(X)→X in C

以下のホムセット同型Φの成分から、単位ηの成分を取り出すことにします。

Φ_A,X:C(F(A), X)→D(A, U(X))

ここに出現するXにF(A)を代入すると：

Φ_A,F(A):C(F(A), F(A))→D(A, U(F(A))

左側のホムセットC(F(A), F(A))はエンドセット〈endset〉（自己射〈endomorphism〉の集合）なので、id_F(A)があります。同型写像Φ_A,F(A)によるid_F(A)の像をη_Aとします。

η_A := Φ_A,F(A)(id_F(A)) : A→U(F(A)) in D

同様に、

(Φ_A,X)^-1:D(A, U(X))→C(F(A), X)

のAにU(X)を代入して、

(Φ_U(X),X)^-1:D(U(X), U(X))→C(F(U(X)), X)

ここから、

ε_X := (Φ_U(X),X)^-1(id_U(X)) : F(U(X))→X in C

としてεの成分ε_Xを定義できます。

今した操作では、単にインデックス族〈indexed family〉 η = (η_A | A∈|D|), ε = (ε_X | X∈|C|) が定義されただけです。これらの射の族が自然変換であるには、いつもの可換図式を示す必要があります。これには、もとの同型写像族 Φ = (Φ_A,X | A∈|D|, X∈|C|) が自然であることを使います。

ηの自然性 η_A;UF(f) = f;η_B を得るには、次の2つの可換図式のなかで、id_F(A)∈C(F(A), F(A)), id_F(B)∈C(F(B), F(B)), F(f)∈C(F(A), F(B)) に注目して図式内の値を追いかけます。εの自然性も同様です。

 C(F(A), F(A)) -(Φ)→ D(A, UF(A))
    |                    |
 C(F(A), F(f))         D(A, UF(f))
    ↓                   ↓
 C(F(A), F(B)) -(Φ)→ D(A, UF(B))


 C(F(B), F(B)) -(Φ)→ D(B, FU(B))
    |                    |
 C(F(f), F(B))         D(f, FU(B))
    ↓                   ↓
 C(F(A), F(B)) -(Φ)→ D(A, FU(B))

転置と反転置

前節の最後では、集合と写像の図式において、特定要素（射になっている）に注目して追いかける方法を使いました。毎回この作業をするのはめんどうなので、公式（要素＝射のあいだの等式）を書き下しておきます。

 g:X→Y in C

 C(F(A), X) -(Φ)→D(A, U(X))
    |                 |
 C(F(A), g)        D(A, U(g))
    ↓                ↓
 C(F(A), Y) -(Φ)→D(A, U(Y))

この可換図式を等式に直します。v∈C(F(A), X)、つまり v:F(A)→X in C とします。可換図式の四角形を左上から時計回りに見ながら、vを追いかけると：

(v:F(A)→X) -(Φ)→ (Φ(v):A→U(X)) -(D(A, U(g)))→ (Φ(v);U(g):A→U(Y))

反時計回りに見ながら、vを追いかけると：

(v:F(A)→X) -(C(F(A), g))→ (v;g:F(A)→Y) -(Φ)→ (Φ(v;g):A→U(Y))

得られる値は等しいので、次の公式が得られます。

Φ(v);U(g) = Φ(v;g)

ここで、表現を簡略にするために次の記法を導入します。

v∈C(F(A), X) に対して、Φ(v)をv^∩と書く。
s∈D(A, U(X)) に対して、Φ^-1(s)をs_∪と書く。

この記法は、次の記事のなかでも使っています。

(-)^∩と(-)_∪が互いに逆であることから次が成立します。

(v^∩)_∪ = v
(s_∪)^∩ = s

C(F(A), X) $\stackrel{\sim}{=}$ D(A, U(X)) という同型から、次のようなペアが生じます。

v∈C(F(A), X) に対して、v←→v^∩ がペアとなる。
s∈D(A, U(X)) に対して、s_∪←→s がペアとなる。

このようなペアの関係も随伴〈adjunct〉と呼ぶようです。ウーン、ひどい。英語では "adjunction", "adjoint", "adjunct" と、紛らわしいけど一応は別な語です。日本語では区別しない（できない）と思います。

比較的最近出たエミリー・リエル〈Emily Riehl〉の教科書では、adjunctを転置〈transposes〉とも呼んでいます。転置という言い方は、デカルト閉圏やトポス、ラムダ計算などでも使う人がいるので、v←→v^∩、s_∪←→s のような関係を互いに転置〈mutually transposed〉であると言いましょう。

ラムダ計算では、ホムセット同型写像をカリー化〈currying〉と呼び、逆写像を反カリー化〈uncurrying〉と呼びます。方向を区別するのは良い習慣なので、v^∩をvの転置〈transpose〉、s_∪をsの反転置〈untranspose | opposite transpose〉と区別することにします。

この節の最初でやったのと同様な方法で、転置と反転置に関する次の公式が得られます。

g:X→Y in C, v:F(A)→X in C に対して、v^∩;U(g) = (v;g)^∩
f:A→B in D, w:F(B)→X in C に対して、f;w^∩ = (F(f);w)^∩
g:X→Y in C, s:A→U(X) in D に対して、s_∪;g = (s;U(g))_∪
f:A→B in D, t:B→U(X) in D に対して、F(f);t_∪ = (f;t)_∪

これらの公式は、絵（ストリング図）を使うと自然に解釈できますが、その話は次の機会にします。（[追記]「お絵描き完全解説」参照。[/追記]）

ニョロニョロ方式の定義

前々節の議論により、ホムセット同型の族 (Φ_A,X | A∈|D|, X∈|C|) であって、適当な関手のあいだの自然同型となっているものから、単位 η = (η_A | A∈|D|) と余単位 ε = (ε_X | X∈|C|) と呼ばれる自然変換が引っ張り出せることが分かりました。

(C, D, F, U, Φ)から、(C, D, F, U, η, ε)へと舞台を移せたわけです。しかしさらに、ηとεのあいだの特定の関係があることが要請されます。それがニョロニョロ関係式です。

(η*F);(F*ε) = F^
(U*η);(ε*U) = U^

図式順記法のままで成分表示を作ると：

A.[(η*F);(F*ε)] = A.F^
X.[(U*η);(ε*U)] = X.U^

DOTN二号記法で少し計算すると：

   A.[(η*F);(F*ε)]
 = A.(η*F);A.(F*ε)
 = (A.η.F);(A.F.ε)

   A.F^
 = (A.F)^

よって、ニョロニョロ関係その1は、
 (A.η.F);(A.F.ε) = (A.F)^

同様に、ニョロニョロ関係その2は、
 (X.U.η);(X.ε.U) = (X.U)^

反図式順で成分表示を書けば：

ε_F(A) $\circ$ F(η_A) = id_F(A)
U(ε_X) $\circ$ η_U(X) = id_U(X)

ウーム、毎度言ってるけど、右から左に逆行でデコボコしていて見にくい（醜い）。

ニョロニョロ関係式（の成分表示）も、ホムセット同型Φの性質と単位／余単位の定義から出ます。前節の最後で示した公式を繰り返し使えばいいのですが、絵（ストリング図）で計算すれば楽です。絵算（pictorial/graphical/diagrammatic calculation）の話はいずれまとめてする予定です（今日はしない）。（[追記]「お絵描き完全解説」参照。[/追記]）

頑張れば、(C, D, F, U, Φ)による随伴系の定義と、(C, D, F, U, η, ε)による随伴系の定義が同値であることが分かります。つまり、ホムセット同型に基づいて定義しても、単位／余単位で定義しても、どっちでも同じ概念を定義できることになります。

ニョロニョロ方式のメリット

ホムセット同型方式とニョロニョロ方式のどちらがいいかは、利用場面によるので一概には言えません。ここでは、ニョロニョロ方式のメリットを述べることにします。

まず、ニョロニョロ方式では、随伴系を規定している法則が等式である点はメリットです。たいていの代数構造は等式的に定義されています*3。我々は等式の扱いには十分に慣れています。よって、等式による定義は扱いやすいのです。

「モノイド圏の随伴性を“豊饒圏の圏”の随伴性に持ち上げる：計画編」では、手順だけ示して実際の計算をしてないのですが、2-関手が縦結合・横結合・等式を保存するなら、等式的に定義される随伴系も保存される、というアイディアに基づいて方針を考えています。

次なるメリットは、等式が表現していることをビジュアルに表現できることです。ビジュアルな表現＝絵は直感的に理解しやすいものです。もちろんこれは、ニョロニョロ等式がワイヤーの引き伸ばしとして図示できることを指しています。絵（ストリング図）からの直感に従うと、例えば、随伴系の全体が圏Adjを作ることはほぼ自明になります。Adjの対象は圏で、Adjの射は (F -| U):C→D という形の随伴系です。

絵が描けるので、随伴系の計算は絵算（pictorial/graphical/diagrammatic calculation）に持ち込めます。絵算が事態を自明化する力に関しては次の記事を見てください。