専門用語においても、同義語・類義語、表記のゆれなどは相当にあります。「こんな言い方もある、あんな言い方もある」と列挙していると、ときに長大なリストになってしまうことがあります。列挙する代わりに正規表現を使うとコンパクトに記述できます。
正規表現により、用語のバリエーションを記述する方法を説明します。なお、「正規表現が何であるか」を知らなくてもかまいませんし、その説明もしません。もし興味があれば、次の記事を参照してください。
- BNF記法入門(1)(19年前!の記事が残っていた)
- この機会にマスターしようぜ、正規表現、構文図、オートマトン
- BNF、EBNF、ABNF、まー正規表現だな
内容:
選択肢と省略可能
基本は次の二種類の書き方です。
- 選択肢: {A | B}
AもBも同じ意味なので、どちらか一方を好きに選んでよいことを表します。選択肢がもっとたくさんあるときは、{A | B | C}、{A | B | C | D} のように書きます。 - 省略可能: {A}?
Aは省略してもよいことを表します。
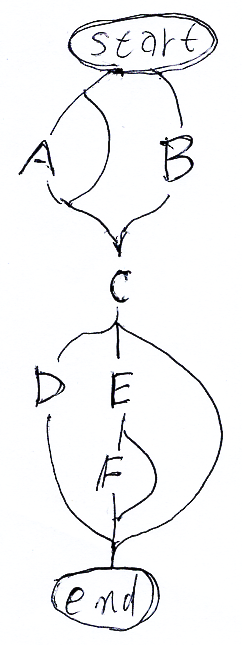
選択肢と省略可能を組み合わせて使ってもかまいません。{{A}? | B}C{D | E{F}?}? が表す語(文字列)をすべて列挙してみると次のようになります。
- ACD
- ACEF
- ACE
- AC
- CD
- CEF
- CE
- C
- BCD
- BCEF
- BCE
- BC
列挙するときは、次のような図を描いて、startからendに至る道を漏れなくたどるようにすると便利です。
具体例
具体例を出しましょう。
例 1
線形代数の文脈で、f:V→V という形(域と余域が同じ)線形写像を次のように呼ぶと約束したとしましょう。
- {線形 | 線型}?{変換 | 自己写像}
この表現が表す語を列挙すると、
となります*1。これらの用語を許す理由は、例えば次のようになるでしょう。
例 2
- {形式{的}? | フォーマル}?{体系 | システム}
これを展開すると:
- 形式的体系
- 形式的システム
- 形式体系
- 形式システム
- フォーマル体系
- フォーマルシステム
- 体系
- システム
「形式システム」、「フォーマル体系」はあまり聞きませんが、別に悪くはないでしょう。
例 3
- {関数 | 演算{子}?}{記号 | 名}?
これを展開すると:
想定される文脈は、形式体系における言語の定義ですね。記号と実体(例えば、関数記号と関数そのもの)を混同するのはマズイのですが、「関数記号」を「関数」と呼んでしまうことは珍しくないので、その習慣を反映して「関数記号」も「関数」も同義語扱いしています。
例 4
- {一貫性 | 整合性}{公理 | 等式 | 関係 | 恒等式 | 制約 | 法則}
これを展開すると:
これは、"coherence axiom"の翻訳語です。coherence → {一貫性 | 整合性} は訳語のゆれですが、英語でも次のバリエーションがあります。
- coherence {axiom | equation | relation | identity | constraint | law}
英語と日本語での例
次の例は、セミナーで出したことがあります。
- {{X-}?{parametrized | indexed}}? family {of Ys}?
先に、この表現を図にしたものを示しましょう。
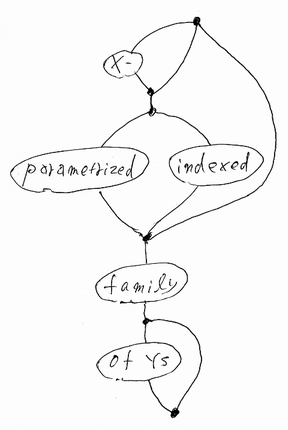
この図を見ながら、上記の表現が表す語を列挙します。
- X-parametrized family of Ys
- X-parametrized family
- X-indexed family of Ys
- X-indexed family
- parametrized family of Ys
- parametrized family
- indexed family of Ys
- indexed family
- family of Ys
- family
この例は英語でしたが、日本語に翻訳すると:
- {{X {の|で|-}? }? {パラメータ | インデックス | 添字} { {付き | 付けられた}? }? {Yの}? }? {ファミリー | 族}
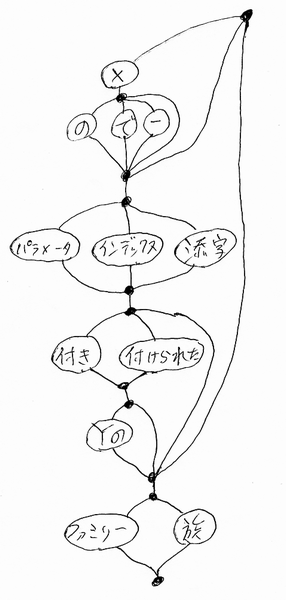
全部列挙するのは大変なので、数個だけ挙げると:
- Xのパラメータ付きYのファミリー (日本語としてやや不適切)
- Xのパラメータ付きYの族 (日本語としてやや不適切)
- Xのパラメータ付きファミリー (日本語として曖昧)
- ...
- ...
- ファミリー
- 族
日本語になると、組み合わせ方によっては、不適切な語や曖昧な語が出てきてしまいます。「Xでインデックス付けられたYの族」あたりが(長いけど)適当でしょう。この言葉の意味は「XからYへの写像」と同じです。なんらかのニュアンスを込めてこんな言い方をするのです。
ウンザリする例
Lawvere theory という概念があります。
Lawvere theory の翻訳語としてあり得そうな日本語は次のようでしょう。
- {代数{的}? | ローヴェア | Lawvere | {ローヴェア | Lawvere}{の}?代数{的}?}{理論 | セオリー | {理論 | セオリー}?圏}
展開すると:
- 代数的理論
- 代数的セオリー
- 代数的理論圏
- 代数的セオリー圏
- 代数的圏
- 代数理論
- 代数セオリー
- 代数理論圏
- 代数セオリー圏
- 代数圏
- ローヴェア理論
- ローヴェアセオリー
- ローヴェア理論圏
- ローヴェアセオリー圏
- ローヴェア圏
- Lawvere理論
- Lawvereセオリー
- Lawvere理論圏
- Lawvereセオリー圏
- Lawvere圏
- ローヴェアの代数的理論
- ローヴェアの代数的セオリー
- ローヴェアの代数的理論圏
- ローヴェアの代数的セオリー圏
- ローヴェアの代数的圏
- ローヴェアの代数理論
- ローヴェアの代数セオリー
- ローヴェアの代数理論圏
- ローヴェアの代数セオリー圏
- ローヴェアの代数圏
- ローヴェア代数的理論
- ローヴェア代数的セオリー
- ローヴェア代数的理論圏
- ローヴェア代数的セオリー圏
- ローヴェア代数的圏
- ローヴェア代数理論
- ローヴェア代数セオリー
- ローヴェア代数理論圏
- ローヴェア代数セオリー圏
- ローヴェア代数圏
- Lawvereの代数的理論
- Lawvereの代数的セオリー
- Lawvereの代数的理論圏
- Lawvereの代数的セオリー圏
- Lawvereの代数的圏
- Lawvereの代数理論
- Lawvereの代数セオリー
- Lawvereの代数理論圏
- Lawvereの代数セオリー圏
- Lawvereの代数圏
- Lawvere代数的理論
- Lawvere代数的セオリー
- Lawvere代数的理論圏
- Lawvere代数的セオリー圏
- Lawvere代数的圏
- Lawvere代数理論
- Lawvere代数セオリー
- Lawvere代数理論圏
- Lawvere代数セオリー圏
- Lawvere代数圏
カタカナ表記のバリエーション(ローヴェル、ロウヴィエールとか)、音引き、ナカグロなどのゆれも考えると、さらに増えます。ウゲーッ。