ストリング図とストライプ図 - 檜山正幸のキマイラ飼育記 (はてなBlog)

昨日の記事の最後の節（付録）「図式思考の例として、ラックス・モノイド関手について考えてみる // ストリング図とストライプ図」の続きです。

内容：

自然変換ストリング図と関手ストリング図
ストリング図書き換え
ストライプ図

自然変換ストリング図と関手ストリング図

単に「ストリング図」と言ってきましたが、二種類のストリング図が登場してましたね。「自然変換、関手、圏」を表すストリング図を自然変換ストリング図〈natural transformation string diagram〉、「関手、圏」を表すストリング図を関手ストリング図〈functor string diagram〉と呼んで区別することにします。

自然変換ストリング図と関手ストリング図では、各次元の図形〈セル〉が表すものが違います。

	自然変換ストリング図	関手ストリング図
エリア（2次元）	圏	（なし）
ワイヤー（1次元）	関手	圏
ノード（0次元）	自然変換	関手

下の図は、「図式思考の例として、ラックス・モノイド関手について考えてみる」に出てきた自然変換ストリング図と関手ストリング図です。次元が食い違ってます。

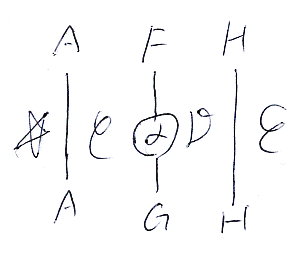
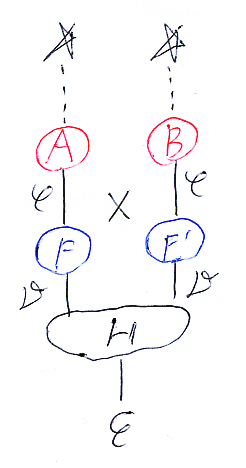
ストライプ図も含めて、縦結合、横結合、直積の方向に関しては：

	自然変換ストリング図	関手ストリング図	ストライプ図
縦結合方向	上から下に縦	（なし）	上から下に縦
横結合方向	左から右に横	上から下に縦	奥から手前
直積方向	手前から奥	左から右に横	左から右に横

次はストライプ図の例です。

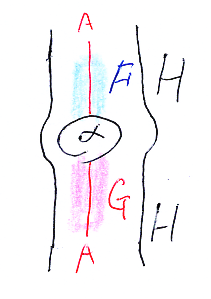
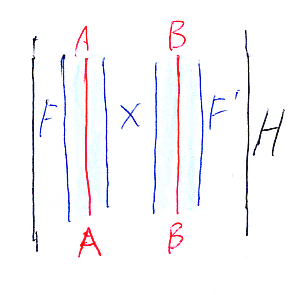
それぞれの描画法ごとに、次元と方向の使い方がマチマチです。これが混乱・困惑の原因になってますが、一方で、文字通り多面的な／多方向からの見方をする助けにもなっています。

ストリング図書き換え

昨日の「図式思考の例として、ラックス・モノイド関手について考えてみる」で紹介した、本来の3次元ストリング図書き換えでは、自然変換を2次元図の書き換えとみなします。

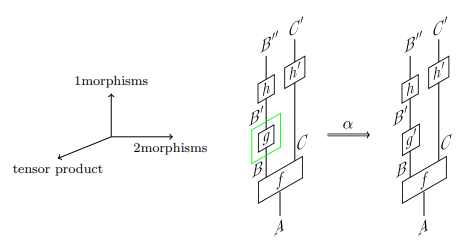
方向の使い方は次のようです。（上のバートレットの図では横結合が下から上ですが、僕は上から下です。）

	自然変換ストリング図	3Dストリング図書き換え
縦結合方向	上から下に縦	奥から手前
横結合方向	左から右に横	上から下に縦
直積方向	手前から奥	左から右に横

ストリング図書き換えを2次元内に描くときは、奥から手前の縦結合方向を、2次元内に適当に収めます。次の図は、「図式思考の例として、ラックス・モノイド関手について考えてみる」の図をわずかに変更したもので、ラックス・モノイド関手の結合律を表す図です。β1, β2, β3, γ1, γ2, γ3 と名前が付けられた矢印は書き換え（自然変換）を表します。

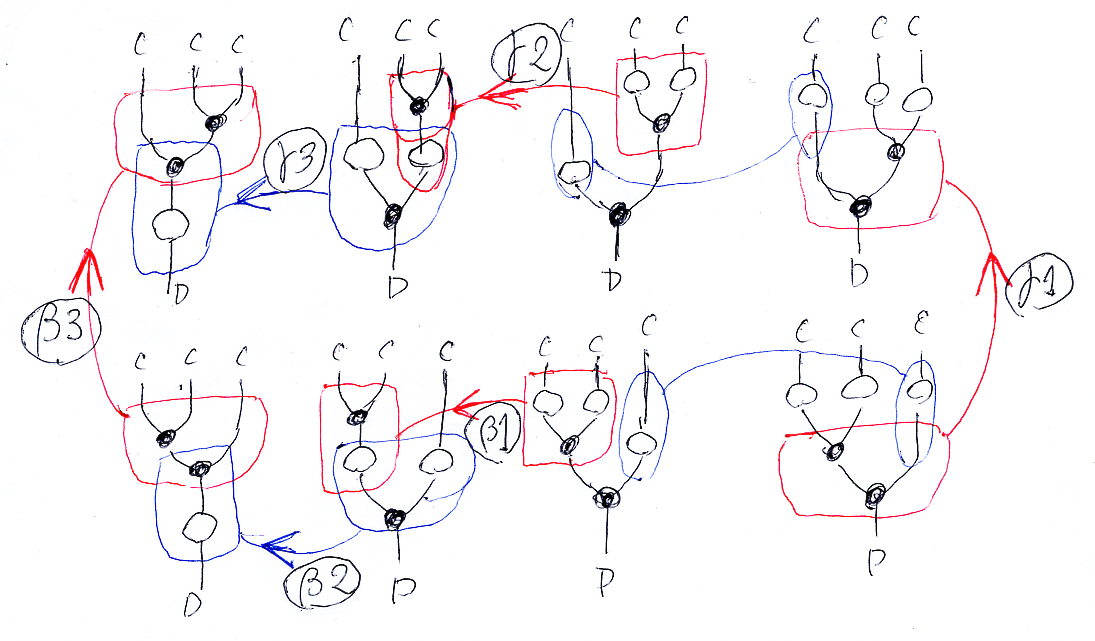
ラベル付けが誤解を招きそうなので注意しておくと； β1, β2, β3, γ1, γ2, γ3 は、ストリング図の一部の書き換えにラベル付けしたのではなくて、ストリング図全体の書き換えを意味します。例えば、β3は、下段1番のストリング図全体を上段1番のストリング図に書き換える自然変換の名前です。

ストライプ図

前節のラックス・モノイド関手の結合律を表すストリング図書き換えを、ストライプ図で描くと以下のようになります。ストリング図書き換えの下段4番から上段1番に至る2つの書き換えパスは等しいことを意味します。ストリング図書き換えの、「上段4番 → 上段3番」と「下段4番 → 下段3番」の書き換えはストライプ図には現れません（奥行きの前後を表現できないので）。

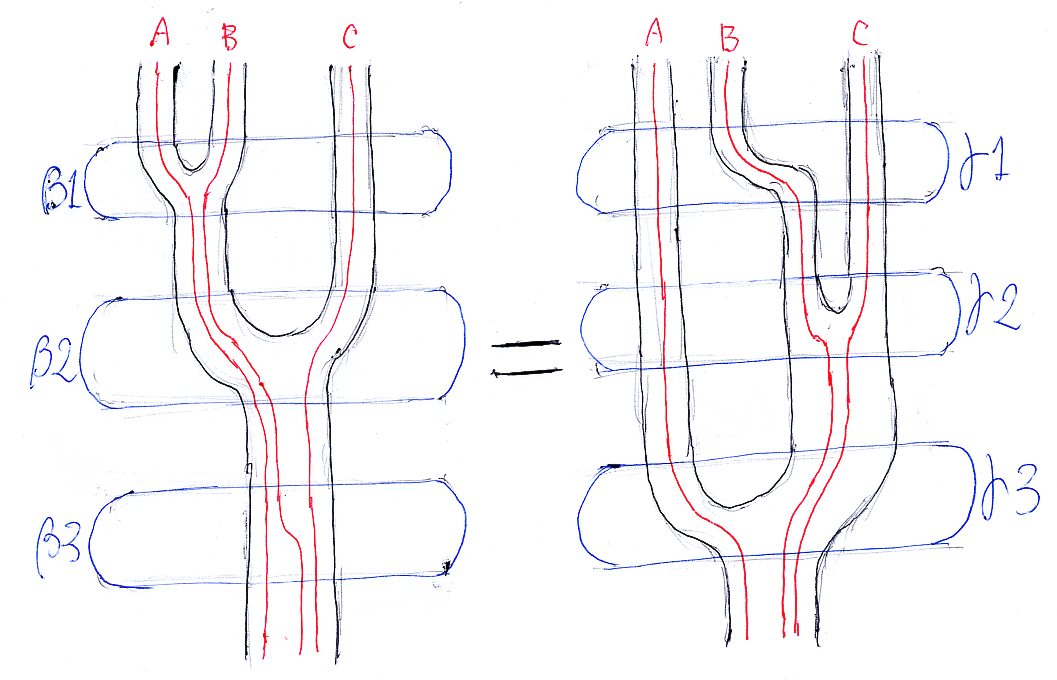
ストリング図書き換えの個々のストリング図は、ストライプ図では単純でストレートなストライプ模様（シース*1に包まれた芯線〈心線〉の並び）になります。書き換え（自然変換）が曲がりや合流として描かれます。

例えば、ストリング図書き換えの下段4番の図は、ストライプ図等式左辺の最上部パーツに対応します（次の図）。

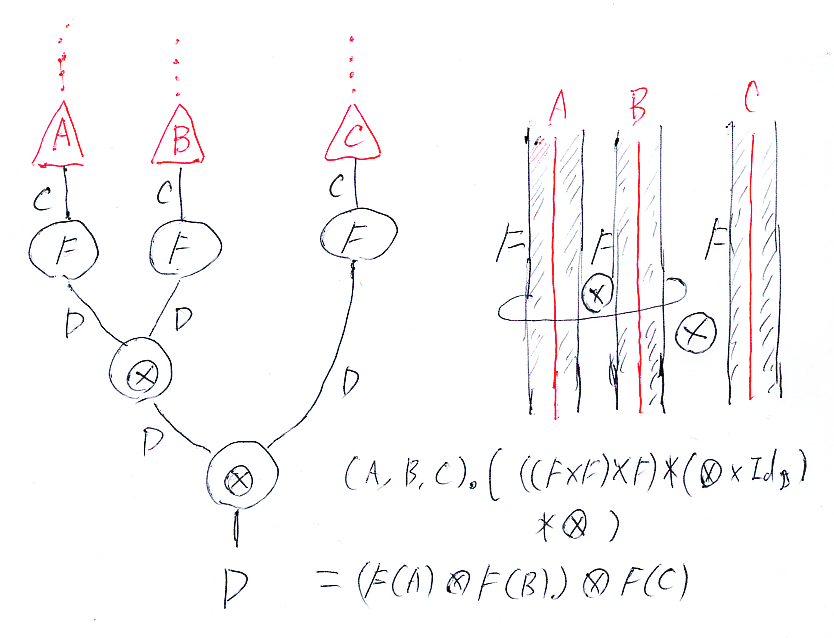
ストライプ図を描くときは、圏Cの3つの対象 A, B, C を選びます。A, B, C がストライプ図ケーブル（シースに包まれたワイヤー）の芯線〈心線〉になります。

関手の組み合わせ ((F×F)×F)＊( $\otimes$ ×Id)＊ $\otimes$ に、公平3-タプル*2(A, B, C) を渡すと、値は（普通の書き方で）(F(A) $\otimes$ F(B)) $\otimes$ F(C) になります。ストリング図では (A, B, C).( ((F×F)×F)＊( $\otimes$ ×Id)＊ $\otimes$ ) という構成・構造が描かれ（ドットは図式順の適用）、ストライプ図では単純化した結果 (F(A) $\otimes$ F(B)) $\otimes$ F(C) が描かれます。