1-圏(通常の圏)のなかでスパンを考えた場合、スパンのあいだの射の定義は簡単です。2-圏のなかだと、スパンの射の定義も難しくなります。「環境付き計算と依存アクテゴリー 1/n // 2-圏内のスパンのあいだの射」で述べたように、1-圏と2-圏では事情が違ってくるのです。具体例で説明します。$`\newcommand{\mrm}[1]{ \mathrm{#1} }
\newcommand{\cat}[1]{ \mathcal{#1} }
\newcommand{\In}{\text{ in }}
%\newcommand{\u}[1]{\underline{#1}}
\newcommand{\o}[1]{\overline{#1}}
\newcommand{\twoto}{ \Rightarrow }
\newcommand{\id}{ \mathrm{id} }
%\newcommand{\hyp}{\text{-} }
`$
内容:
ハブ記事:
1-圏のなかのスパン
$`\cat{C}`$ を1-圏(通常の圏)だとします。$`\cat{C}`$ 内のスパン〈span〉は、次の形をした $`\cat{C}`$ の図式です。
$`\quad \cdot \leftarrow \cdot \rightarrow \cdot \:\In \cat{C}`$
スパンの各部位〈構成素〉は、左足〈left foot〉、左脚〈left leg〉、ボディ〈body〉(またはヘッド〈head〉)、右脚〈right leg〉、右足〈right foot〉です。見たまんまなので説明は不要でしょう。
スパンを $`X`$ と書いたとき、ここでは次の書き方を使います。
- $`X`$ のボディを $`\o{X}`$ と書く。
- $`X`$ の左脚を $`X_L`$ と書く。
- $`X`$ の右脚を $`X_R`$ と書く。
左足は $`\mrm{cod}(X_L)`$ 、右足は $`\mrm{cod}(X_R)`$ として決まります。スパンを構成素の組として書くときは次のように書くと約束します。
$`\quad X = (\o{X}, X_L, X_R)`$
左足と右足が一致しているスパンを自己スパン〈endo-span〉と呼びます。足が $`A`$ である $`\cat{C}`$ 内のすべての自己スパンの集合を $`\mrm{EndSpan}[A](\cat{C})`$ とします。$`\cat{C}`$ がプルバックを持てば、$`\mrm{EndSpan}[A](\cat{C})`$ にプルバックから定義される結合〈composition〉演算を入れることができます。が、今回はスパンの結合を使わないので、$`\mrm{EndSpan}[A](\cat{C})`$ は単なる集合としておきます。
$`X, Y \in \mrm{EndSpan}[A](\cat{C})`$ のとき、スパンのボディのあいだの射 $`f : \o{X} \to \o{Y} \In \cat{C}`$ が次の図式を可換にするとき、スパン〈自己スパン〉のあいだの射〈morphism〉と呼びます。
$`\quad \xymatrix{
{}
& \o{X} \ar[dl]_{X_L} \ar[dr]^{X_R}
\ar[dd]|{f}
& {}
\\
A
& {}
& A
\\
{}
& \o{Y} \ar[ul]^{Y_L} \ar[ur]_{Y_R}
& {}
}\\
\quad \text{commutative }\In \cat{C}`$
図式を以下にようにレイアウトすると見やすいし、二重圏との連絡がよくなります。
$`\quad \xymatrix{
A \ar@{=}[d]
& \o{X} \ar[l]_{X_L} \ar[r]^{X_R}
\ar[d]|{f}
& A \ar@{=}[d]
\\
A
& \o{Y} \ar[l]^{Y_L} \ar[r]_{Y_R}
& A
}\\
\quad \text{commutative }\In \cat{C}`$
スパンのあいだの射の結合は $`\cat{C}`$ における結合と同じです。スパンの恒等射は $`\cat{C}`$ の恒等射として定義できます。このようにして作ったスパン〈自己スパン〉を対象とする圏を $`\cat{EndSpan}[A](\cat{C})`$ とします。スパンの集合とスパンの圏のあいだには次の関係があります。
$`\quad |\cat{EndSpan}[A](\cat{C})| = \mrm{EndSpan}[A](\cat{C})`$
2-圏のなかのスパン
2-圏の話では、多辺形と多角形の違いが重要になってきます。それについては「圏論におけるフレーム充填問題 // n辺形とn角形」を参照してください。
$`\cat{K}`$ を2-圏とします。横結合の図式順演算子記号をアスタリスク '$`*`$' 、縦結合のの図式順演算子記号をセミコロン '$`;`$' とします。2-圏であっても、スパンの定義は1-圏と同じです。次の形状の図式です。
$`\quad \cdot \leftarrow \cdot \rightarrow \cdot \:\In \cat{K}`$
しかし、スパンのあいだの射の定義は複雑になります。参照のため、1-圏の図を再掲します。
$`\quad \xymatrix{
A \ar@{=}[d]
& \o{X} \ar[l]_{X_L} \ar[r]^{X_R}
\ar[d]|{f}
& A \ar@{=}[d]
\\
A
& \o{Y} \ar[l]^{Y_L} \ar[r]_{Y_R}
& A
}`$
1-圏の場合、図の左右の四辺形(この場合は三辺形としても同じ)を埋める方法〈2-射〉は等式〈恒等2-射〉だけです。「図が可換である」の意味は、図のなかの多辺形がすべて等式〈恒等2-射〉で埋められているということです。
2-圏の場合、四辺形を埋める方法〈2-射〉は等式以外に色々あります。「依存アクテゴリーに向けて // 一貫性地獄」で述べたように、多辺形を埋める2-射の緩さ〈looseness | weakness〉と方向は色々あります。スパンの場合の緩さと方向については、「環境付き計算と依存アクテゴリー 1/n // 2-圏内のスパンのあいだの射」で述べています。
ここでは、緩さと方向を具体的にひとつに決めます。スパン〈自己スパン〉の左側の四角形はラックス可換、右側は反ラックス可換だとします。ラックスと反ラックスも約束の問題なので、以下の図の斜め矢印のようだとします。
$`\quad \xymatrix{
A \ar@{=}[d]
\ar@{=>}[dr]
& \o{X} \ar[l]_{X_L} \ar[r]^{X_R}
\ar[d]|{f}
& A \ar@{=}[d]
\\
A
& \o{Y} \ar[l]^{Y_L} \ar[r]_{Y_R}
\ar@{=>}[ur]
& A
}\\
\quad \In \cat{K}`$
左側の四角形を埋める2-射のプロファイルは:
$`\quad X_L \twoto f* Y_L : \o{X} \to A \In \cat{K}`$
右側の四角形を埋める2-射のプロファイルは:
$`\quad f* Y_R \twoto X_R : \o{X} \to A \In \cat{K}`$
スパンのあいだの射には、左右の四角形を埋める2-射も含まれます。つまり、スパン $`X`$ からスパン $`Y`$ への射 $`F`$ は次の構成素を持ちます。
$`\quad F = (\o{F}, F_L, F_R)\\
\text{Where}\\
\quad \o{F} : \o{X} \to \o{Y} \In A \cat{K}\\
\quad F_L :: X_L \twoto \o{F} * Y_L : \o{X} \to A \In \cat{K}\\
\quad F_R :: \o{F}* Y_R \twoto X_R : \o{X} \to A \In \cat{K}
`$
1-圏の場合は、$`f = \o{F}`$ しか問題になりませんでしたが、2-圏では2-射 $`F_L, F_R`$ が重要になります。
$`F_L, F_R`$ をストリング図で描けば次のようです。描画方向は上から下、左から右です。背景エリアのラベル($`\o{X}, A`$)は省略しています。
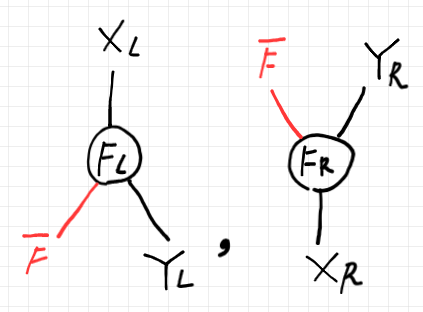
このままでは、射の結合の描画が難しいので、$`F_L`$ は上から下、$`F_R`$ は下から上に変更します(左右の反転はしません)。次のようになります。
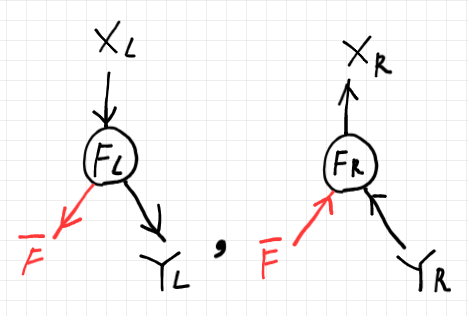
さて、スパンのあいだの射 $`F:X \to Y`$ と $`G:Y \to Z`$ を結合するとします。2-圏 $`\cat{K}`$ 内のペースティング図に展開すると、次のようです。
$`\quad \xymatrix{
A \ar@{=}[d]
\ar@{=>}[dr]|{F_L}
& \o{X} \ar[l]_{X_L} \ar[r]^{X_R}
\ar[d]|{\o{F}}
& A \ar@{=}[d]
\\
A \ar@{=}[d]
\ar@{=>}[dr]|{G_L}
& \o{Y} \ar[l]|{Y_L} \ar[r]|{Y_R}
\ar[d]|{\o{G}}
\ar@{=>}[ur]|{F_R}
& A \ar@{=}[d]
\\
A
& \o{Z} \ar[l]^{Z_L} \ar[r]_{Z_R}
\ar@{=>}[ur]|{G_R}
& A
}\\
\quad \In \cat{K}`$
スパンの射の結合を、ストリング図のワイヤリング操作として描くなら次のようです。
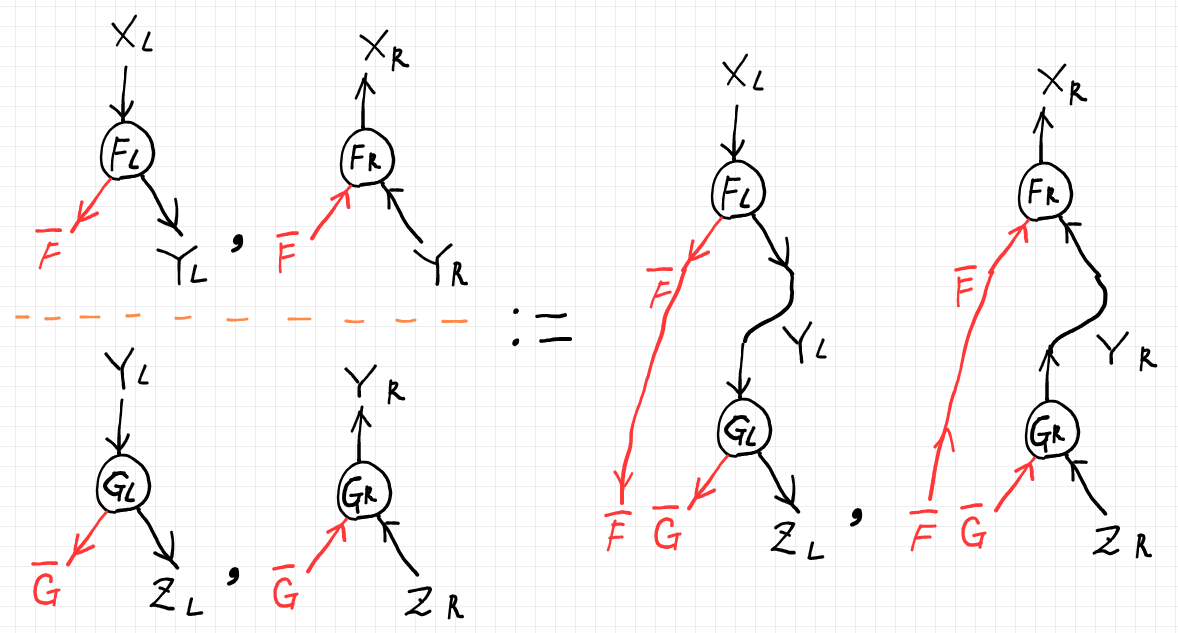
ここで、オレンジ色の破線が結合を表します。$`Y_L, Y_R`$ のワイヤーを繋ぐことが結合です。テキストで書くならば:
$`\quad (F ; G)_L := F_L ; (\o{F} * G_L)\\
\quad (F ; G)_R := (\o{F}* G_R) ; F_R
`$
ここでのアスタリスクはヒゲ結合〈whiskering〉です。
1-圏の場合は「図式が可換になる」で済んでいたことが、2-圏内の図式では、多辺形の境界内部を埋める2-射の緩さと方向の選び方が多様になるので複雑化します。スパンのあいだの射の定義の複雑化はその一例です。