Lean(最新版はLean 4)は強力な型システムを備えた汎用プログラミング言語です。そればかりではなくて、証明支援系としての機能も同一の型システムをベースにして実現しています。AgdaやCoqもまた、型システムに基づく証明支援系/プログラミング言語です。
これら現存する最強の型システムでは、“型宇宙”がサポートされています。
- Agda "Sort System" https://agda.readthedocs.io/en/v2.6.2.2/language/sort-system.html#sort-system
- Coq "Polymorphic Universes" https://coq.inria.fr/refman/addendum/universe-polymorphism.html
- Lean "Universes" https://leanprover.github.io/reference/expressions.html
型理論、集合論、圏論で共に利用できるような宇宙概念について考えてみます。宇宙と直結した圏として銀河を導入します。$`\newcommand{\mrm}[1]{ \mathrm{#1} }
\newcommand{\cat}[1]{\mathcal{#1} }
`$
内容:
シリーズ記事:
- 最近の型理論: 宇宙と世界、そして銀河 (この記事)
- 最近の型理論: 宇宙・世界・銀河 もう少し
- 最近の型理論: 型理論の構文論と意味論
- 最近の型理論: 依存型理論で述語論理が出来てしまう理由
- 最近の型理論: 型判断/シーケントの意味論に向けて
- 最近の型理論: 外部化手法のもとでのパイ型と指数型
- 最近の型理論: デカルト閉圏の外部化・内部化とスノーグローブ現象
- 最近の型理論: 宇宙より銀河
- 最近の型理論: 具体的・構文的なコンテキスト
- 最近の型理論: 拡張包括構造を持ったインデックス付き圏
関連記事:
宇宙と世界
語感としては、世界より宇宙のほうが広い感じがしますが、ここでは、世界は宇宙(と後述の銀河)の集まりだとします。$`\mathscr{W}`$ がひとつの世界〈a world〉だとすると、世界 $`\mathscr{W}`$ のなかにはたくさんの宇宙が入っています。宇宙のなかでも特に重要な役割を演じているコア宇宙の全体を $`\mathscr{W}_\mrm{Core}`$ とします。世界には、コア宇宙ではない宇宙も存在しますが、先にコア宇宙を説明します。
世界のコア宇宙〈core universe〉($`\mathscr{W}_\mrm{Core}`$ の要素)はグロタンディーク宇宙です。グロタンディーク宇宙は、集合論〈ZFC集合論〉で“集合”と認められる集合ですが、そのなかで集合論的構成が自由に行えるような集合です。「集合論的構成が自由に行える」とはどんなことかは、次の記事を読むと感じがつかめるでしょう。
グロタンディーク宇宙そのものに関しては、以下の過去記事とそこから参照される関連記事になにやら書いています。
グロタンディーク宇宙の系列を選びます。
$`\quad U_0 \in U_1 \in U_2 \in \cdots`$
各宇宙に付けられた番号を、宇宙のランク〈rank〉またはレベル〈level〉と呼びます。
自然数で番号付けられたグロタンディーク宇宙の系列を固定すると、それで世界のコア〈core〉または幹〈trunk〉が決まります。
$`\quad \mathscr{W}_\mrm{Core} = \{U_0, U_1, U_2, \cdots \}`$
なぜ、幹と呼ぶかは最後の説の絵を見ると明らかでしょう。
銀河
集合や型を圏論的に解釈したいなら、世界の構成素をグロタンディーク宇宙(という構造物)だとするより、デカルト閉圏(という構造物)だと考えたほうが便利です。世界のパーツとなるようなデカルト閉圏を“銀河”と呼ぶことにします。銀河であるためには幾つかの条件を満たす必要があります。
まず、グロタンディーク宇宙と圏の関係から説明します。$`U`$ がグロタンディーク宇宙のとき、$`A\in U`$ である $`A`$ を$`U`$-小集合〈$`U`$-small set〉、$`B \subseteq U`$ である $`B`$ を$`U`$-クラス〈$`U`$-class〉と呼びます。「大きい集合〈大集合〉」という言葉は、小さくない集合なのか、小さいとは限らない集合なのか分からない(人により違う)ので使いません。「クラス」も、とんでもなく多義語だという点で望ましくはないですが、集合論では定番の用語です。
圏 $`\cat{C}`$ が、次の条件を満たすとき、$`U`$-小圏〈$`U`$-small category〉といいます。
- $`|\cat{C}| \in U`$
- $`\mrm{Mor}(\cat{C}) \in U`$
次の条件を満たすときは$`U`$-局所小圏〈$`U`$-locally-small category〉といいます。
- $`|\cat{C}| \subseteq U`$
- $`\forall A, B \in |\cat{C}|.\, \cat{C}(A, B) \in U`$
$`U`$-小圏は常に$`U`$-局所小圏ですが、逆は成立しません。
$`U`$-局所小圏 $`\cat{C}`$ が離散完備〈discretely complete〉だとは、
- 任意の $`A\in U`$ を域とする任意の写像 $`F:A \to |\cat{C}|`$ を離散図式とみて、図式の極限が存在する。
同様に、離散余完備〈discretely co-complete〉とは:
- 任意の $`A\in U`$ を域とする任意の写像 $`F:A \to |\cat{C}|`$ を離散図式とみて、図式の余極限が存在する。
グロタンディーク宇宙 $`U`$ に対して、$`U`$-局所小圏 $`\cat{C}`$ がデカルト閉圏であり、離散完備かつ離散余完備なとき、$`\cat{C}`$ を$`U`$ 上の銀河〈galaxy over $`U`$〉、あるいはより短く$`U`$-銀河〈$`U`$-galaxy〉と呼ぶことにします。
銀河は、論理や型理論を構成するためのロジカル・フレームワークの意味領域のような役割を演じます。
世界の構造
世界〈world〉$`\mathscr{W}`$ は、コア宇宙の系列 $`\mathscr{W}_\mrm{Core}`$ と銀河の集まり $`\mathscr{W}_\mrm{Galx}`$ から構成されます。コア〈幹〉 $`\mathscr{W}_\mrm{Core}`$ と銀河達 $`\mathscr{W}_\mrm{Galx}`$ のあいだには次の関係があります。
- 世界 $`\mathscr{W}`$ の任意の銀河 $`\cat{C}`$ に対して、唯一つのコア宇宙 $`U`$ が決まり、$`\cat{C}`$ は$`U`$-銀河($`U`$-局所小な離散完備・離散余完備なデカルト閉圏)である。
- 世界 $`\mathscr{W}`$ の任意のコア宇宙 $`U`$ に対して、唯一つの銀河 $`{\bf Set}_U`$ が決まる。
「銀河」は、前節で定義した「$`U`$-局所小な離散完備・離散余完備なデカルト閉圏」の意味と、世界の構成素(の役割名)の意味で使っています。この2つの用法は違う概念を表しますが、同じ言葉「銀河」を使います。
[/補足]
一番目の条件から決まるコア宇宙 $`U`$ を、銀河 $`\cat{C}`$ の台宇宙〈underlying universe〉と呼びましょう。([追記 date="当日数時間後"]基盤宇宙〈underpinning universe〉に変更するつもり。[/追記])
- 銀河 $`\cat{C}`$ の対象クラス $`|\cat{C}|`$ は、台宇宙 $`U`$ のクラスである(小集合とは限らない)。
- 銀河 $`\cat{C}`$ のホムセット $`\cat{C}(A, B)`$ は、台宇宙 $`U`$ の小集合である。
$`{\bf Set}_U`$ は、$`U`$-小集合を“集合”とみなした集合圏です。
- $`|{\bf Set}_U| = U`$
- $`\forall A, B \in |{\bf Set}_U|.\, {\bf Set}(A, B) \in U`$
- $`{\bf Set}_U`$ は、$`U`$上の銀河である。
- 銀河 $`{\bf Set}_U`$ の台宇宙は $`U`$ である。
コア宇宙は番号(宇宙レベル)$`i`$ を持つので、$`U = U_i`$ と書けます。$`{\bf Set}_{U_i}`$ を $`{\bf Set}_{\#i}`$ と略記します。
コア宇宙に対応する集合圏 $`{\bf Set}_{\#i} \text{ for some }i\in {\bf N}`$ をコア銀河〈core galaxy〉と呼びます。世界には、コア銀河ではない銀河もあるかも知れません。コア銀河ではない銀河を非コア銀河〈non-core galaxy〉と呼びます。
一般に、世界 $`\mathscr{W}`$ の銀河 $`\cat{C}`$ の対象クラス $`|\cat{C}|`$ を宇宙と呼びます。世界には、コア銀河ではない銀河もあるかも知れないので、非コア宇宙〈non-core universe〉もあり得ます。
- 世界〈a world〉を構成する銀河には、コア宇宙に対応するコア銀河(必須)と、非コア銀河がある(かも知れない)。
- 世界〈a world〉を構成する宇宙には、コア宇宙(必須)と、非コア宇宙がある(かも知れない)。
型とインスタンス
$`U`$ が世界 $`\mathscr{W}`$ のコア宇宙のとき、適当な番号 $`i`$ により $`U = U_i`$ と書けます。このとき、$`U_{i + 1}`$ を $`U'`$ と略記します。適当なコア宇宙を“デフォルトの宇宙”として選んだとき、$`{\bf Set}_U = {\bf Set}_{U_i}`$ を単に $`{\bf Set}`$ と書きます。また、$`{\bf Set}_{U'} = {\bf Set}_{U_{i + 1}}`$ を $`{\bf SET}`$(すべて大文字)で表します。
コアとは限らない(が、コアであってもかまわない)一般の宇宙を $`S, T`$ などで表します。宇宙は銀河の対象クラスとして定義されるので、
- 世界 $`\mathscr{W}`$ の任意の宇宙 $`T`$ は、銀河 $`\cat{C}`$ により $`T = |\cat{C}|`$ と書ける。
- 特に、コア宇宙 $`U`$ は $`U = |{\bf Set}_U|`$
異なる2つの銀河 $`\cat{C}, \cat{D} \in \mathscr{W}_\mrm{Galx}`$ に対して、
$`\quad T = |\cat{C}| = |\cat{D}|`$
であることは許します。宇宙は単体で扱うものではなくて、銀河から決まる構造として、あるいは銀河の一部分として扱います。
世界のなかで、銀河の対象(宇宙の要素)を型〈type〉と呼びます。宇宙(銀河の対象クラス)は、他の銀河(コア銀河になる)の対象になっているので、この意味で“宇宙は型”です。
$`A`$ が型のとき、$`A\in T`$ となる宇宙(コア宇宙とは限らない)$`T`$ があり、$`T = \cat{C}`$ である銀河 $`\cat{C}`$ があります。型理論の意味で $`x: A`$ と書いたとき、$`x`$ は型 $`A`$ のインスタンス〈instance〉と呼びます。インスタンスは、値、要素、データ、オブジェクト、項などとも呼びますが、ここでは「インスタンス」を使います。
型 $`A`$ は集合として要素を持つかも知れませんが、
- 型 $`A`$ のインスタンスは、(集合としての)$`A`$ の要素としては定義しない
ので注意してください。インスタンスの定義は以下のとおりです。
- 型 $`A`$ が所属する銀河 $`\cat{C}`$ のホムセット $`\cat{C}({\bf 1}, A)`$ の要素を、型 $`A`$ のインスタンスと呼ぶ。
$`{\bf 1}`$ は圏 $`\cat{C}`$ の(特定された)終対象です。$`\cat{C}`$ はデカルト閉圏だったので、終対象は存在します。
型 $`A`$ のインスタンス全体の集合を $`\mrm{Inst}(A)`$ とします。
$`\quad \mrm{Inst}(A) := \cat{C}({\bf 1}, A)`$
型 $`A`$ を含む銀河 $`\cat{C}`$ は、台宇宙として(一意的な)コア宇宙 $`U`$ を持ち、ホムセットは$`U`$-小集合です。したがって、
$`\quad \mrm{Inst}(A) \in U \in \mathscr{W}_\mrm{Core}`$
まとめ
世界の構造は、次のようなツリーとして描けるでしょう。
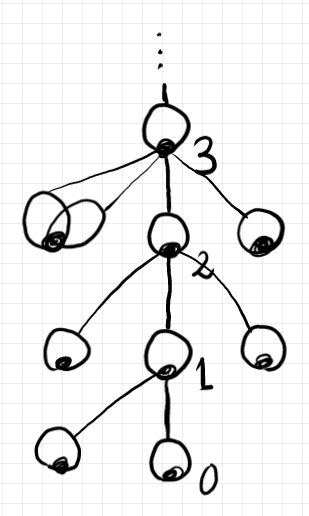
白いマルが銀河で、銀河内部の黒丸は宇宙(銀河の対象クラス)です。異なる銀河が同一の宇宙を共有していることもあります。下から上に番号がふられた真ん中の系列がコア宇宙/コア銀河の系列で、ツリーの幹になります。枝(一部は幹)であるエッジは、銀河とその台宇宙を結んでいます。各銀河のなかに型とインスタンス達が棲んでいます。
北欧神話に登場するユグドラシル〈世界樹〉は、「世界を体現する巨大な木」とのことですが、上記のツリーは、集合論/型理論/圏論の世界を体現するユグドラシルです。
型理論における宇宙については、以下の2つの論文にまとまっています。
- Title: On Universes in Type Theory
- Author: Erik Palmgren
- Pages: 14p
- URL: http://www2.math.uu.se/~palmgren/universe.pdf
- Title: Notes on Universes in Type Theory
- Author: Zhaohui Luo
- Pages: 8p
- URL: https://www.cs.rhul.ac.uk/home/zhaohui/universes.pdf