このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

最近の型理論： 型理論の構文論と意味論

雑記／備忘

記事タイトルの「最近の」は、「理論的には古くから知られていても、実用的利用は最近になって出てきた」といった意味です。さらに具体的な特徴として、「階層化された宇宙達を備えた型理論」のことです。そのような型理論は、Lean, Agda, Coq などの型システムの背景理論になっています。

この記事では、「階層化された宇宙達を備えた型理論」における構文論と意味論のおおよその枠組みを述べます。以下の過去記事で述べたことを利用します。$`\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\In}{\text{ in }}
\newcommand{\Imp}{\Rightarrow}
\newcommand{\Iff}{\Leftrightarrow}
\newcommand{\hyp}{ \text{－} }
\newcommand{\wrld}[1]{\mathscr{#1}}
\newcommand{\BR}[1]{ \left[\!\left[ {#1} \right]\!\right] }
\newcommand{\Path}{/}
`$

内容：

シリーズ・ハブ記事：

型、宇宙、集合に関する資料

過去記事「最近の型理論： 宇宙と世界、そして銀河」でも言及しましたが、プログラミング言語／証明支援系のドキュメント内の、宇宙に関する記述は：

型理論における宇宙〈型宇宙〉についての解説は：

　

以下、その他の（過去記事で言及しなかった）文献を幾つか紹介します。

型理論とZFC集合論の関係を論じています。階層化された型宇宙を集合論で解釈するために、到達不能基数〈{strongly}? inaccessible cardinal〉を使っています。到達不能基数とグロタンディーク宇宙は事実上同じものですから、型宇宙をグロタンディーク宇宙で解釈していることになります。

Coqの型宇宙を定式化するのが目的のようです。Coq風の型システム／構文によるZFC集合論の記述も書いてあります。これにより、ZFC集合論と型理論は双方向にシミュレート可能だと分かります。

先のワーナー〈Benjamin Werner〉の方法だと、命題の型宇宙が必ず排中律を満たすことになるとのこと。これを緩和するモデルの構成法が書いてあります。純粋に集合論的な構成では無理なので、位相空間を使っています。

Lean 3（Lean 4でもほぼ同じだと思います）の型システムに対する厳密な定式化を展開しています。後半では、ワーナー同様、ZFC集合論のなかに宇宙を含む型システムをエンコードしています。

宇宙より銀河と世界

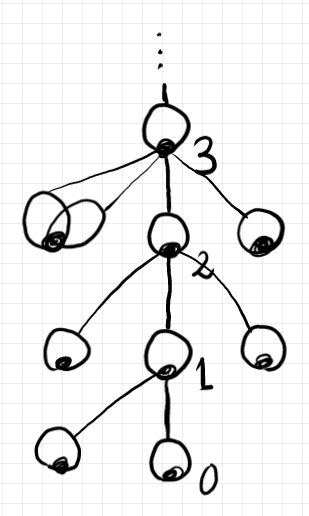
「階層化された宇宙達を備えた型理論」では、まず宇宙〈universe〉達があり、「型は宇宙の要素だ」と考えます。宇宙は、それより一階層上の宇宙の要素なので「宇宙も型だ」となります。次のような感じです。

型　（所属する）→宇宙
　　　　　　　　　型　（所属する）→宇宙
　　　　　　　　　　　　　　　　　　型　（所属する）→宇宙
　　　　　　　　　　　　　　　　　　　　　　　　　　　‥‥

宇宙を持つ型システムのモデルでは、型付け〈タイピング〉を集合論的な所属関係〈membership relation〉に還元して考えています。

集合論的な解釈は必要ではあるのですが、圏論的型理論を展開したいので、宇宙よりは銀河〈galaxy〉（と呼ばれるデカルト閉圏）に重心を移します。$`\cat{C}`$ が銀河のとき、その宇宙は対象のクラス $`|\cat{C}|`$ として定義されます。宇宙は派生的概念で、先に銀河があると考えたいのです。

グロタンディーク宇宙 $`U`$ と対応する集合圏の場合は、$`U \leftrightarrow {\bf Set}_U`$ という“宇宙と銀河の1：1対応”がありますが、一般には、宇宙（圏の対象のクラス） $`|\cat{C}|`$ からデカルト閉圏 $`\cat{C}`$ を再現することは出来ません。宇宙より先に銀河があることが必須の要件になります。

意味論では、記号的表現に対して何らかの事物を対応させます。必要となるありとあらゆる事物を含んだ構造物が世界〈world〉です。世界 $`\wrld{W}`$ は、銀河の集合 $`\wrld{W}_\mrm{Galx}`$ を持ちます。記法を簡略化するため、$`\mrm{Galx} := \wrld{W}_\mrm{Galx}`$ と置きます。

$`\mrm{Galx}`$ の要素は巨大な圏かも知れませんが、$`\mrm{Galx}`$ 自体は小さい集合です。より正確に（かつ分かりやすく）言えば、普通の集合 $`I`$ があって、$`I`$ を使って次のような可逆なインデキシングが出来ます。

$`\quad I \cong \mrm{Galx}\\
\quad I \ni i \mapsto \cat{G}_i \in \mrm{Galx}\:\text{ (bijection)}`$

$`\mrm{Galx}`$ はのっぺらぼうな集合ではなくて、階層構造を持ちます。この階層構造は、順序 $`\preceq`$ で与えられるとします*1。$`\prec`$ は次のように定義します。

$`\quad \cat{C} \prec \cat{D} :\Iff (\cat{C} \preceq \cat{D}\,\land\, \cat{C} \ne \cat{D})`$

階層構造を与える順序は次の性質を持つとします。

$`\quad \forall \cat{C}\in \mrm{Galx}. \exists \cat{D}\in \mrm{Galx}.\\
\qquad \cat{C}\prec \cat{D} \,\land\\
\qquad \forall \cat{E}\in \mrm{Galx}.(\, \cat{C}\prec \cat{E} \Imp \cat{D} \preceq \cat{E} \,)`$

この性質は、任意の銀河に“次の銀河”あるいは“親の銀河”が決まることです（一意的であることが証明できます）。銀河 $`\cat{C}`$ の親の銀河を $`\mrm{UG}(\cat{C})`$ とします -- UG はunderpinning galaxy〈基盤銀河〉からです。

“親が親である”要件のひとつは：

$`\quad |\cat{C}| \in |\mrm{UG}(\cat{C})|`$

これにより、宇宙の系列が再現できます。

$`\quad |\cat{C}| \in |\mrm{UG}(\cat{C})| \in |\mrm{UG}(\mrm{UG}(\cat{C}) )| \in \cdots`$

世界の幹となるコア銀河達 $`{\bf Set}_{U_i}\:i = 0, 1, \cdots`$ 以外の銀河と対応する宇宙があってもかまいません。つまり、世界樹〈ユグドラシル〉は幹だけの直線状ではなくて、枝葉を持ってもいいのです。

世界のなかに存在する事物達

$`\mrm{Galx}`$ は、とある世界の銀河の集合ですが、それぞれの銀河は対象や射を持ちます。世界のなかに存在する事物とは、どれかの銀河の対象か射です。より高次の銀河（n-圏）を考えるときは、とある銀河のk-射が事物〈thing〉となります。

世界のなかに存在する事物を名指しするには、アドレッシング方式が必要です。そのアドレッシング方式として、過去記事「有界な圏論的宇宙と圏論的パス式」で導入した圏論的パス式〈categorical path expression〉を使います。

上記過去記事は、用語「銀河」「宇宙」が、この記事とは少し違う意味で使われていて混乱するかも知れません。圏論的パス式は、ここで改めて定義します。（[追記 date="2023-04-28"]先頭のスラッシュを追加。[/追記]）

  • 銀河 $`\cat{C}`$ は、$`\Path\cat{C}`$ で表す。
  • 銀河 $`\cat{C}`$ の対象 $`A`$ は、$`\Path\cat{C}/A`$ で表す。
  • 銀河 $`\cat{C}`$ の射 $`f:A \to B`$ は、$`\Path\cat{C}/(A, B)/f`$ で表す。
  • 銀河 $`\cat{C}`$ の射のあいだの等式（2-射） $`\alpha :: f \Rightarrow g : A \to B`$ は、$`\Path\cat{C}/(A, B)/(f, g)/\alpha`$ で表す。
  • 銀河 $`\cat{C}`$ のホムセットは、$`\Path\cat{C}/(A, B)`$ で表す。

銀河 $`\cat{C}`$ の親銀河が $`\cat{D} = \mrm{UG}(\cat{C})`$ のとき、親銀河の対象とみなした $`|\cat{C}|`$ は $`\Path\cat{D}/|\cat{C}|`$ と書けます。銀河のホムセットが自分の対象（自己豊穣圏）である場合は $`\Path\cat{C}/(\Path\cat{C}/(A, B))`$ が意味を持ちます。

インターネット上にある事物〈リソース〉がURLで識別できるように、（概念的な）世界 $`\wrld{W}`$ にある事物は圏論的パス式で識別できます。

世界 $`\wrld{W}`$ 内の、圏論的パス式で表現・識別できるすべての事物の集合を $`\mrm{Thing}\,\wrld{W}`$ とします。

[補足]
過去記事「有界な圏論的宇宙と圏論的パス式」では、圏論的パス式にスーパールートを使っていました。過去記事の「銀河」は、高次圏も考慮した、十分に大きなコア銀河（高次銀河）の意味でした。今回の設定では、すべてのコア銀河を使うので、スーパールートとしては世界が適切でしょう。スーパールートも書くなら、例えば次のようになります。

$`\quad \Path/\wrld{W}/\cat{C}/(A, B)/(f, g)/\alpha`$
[/補足]

付値

意味論とは、記号的表現＝構文的対象物〈syntactic object〉に、世界の事物を割り当てる行為です。このとき、意味の値達が居る領域として、単一の集合や単一の圏では不十分なのです。なので、たくさんの圏〈銀河〉を含む世界を準備したのです。

構文的対象物を構成するアトミックな要素は名前〈name | identifier〉です。名前は名前の集合 $`\mrm{Name}`$ の要素だとします。名前の集合は、名前が不足しないように、可算無限集合であることを要請します（実際に使用するのはそのうち有限個です）。名前の実体が何であるかは何も決めてないので、名前の集合とは「任意の可算無限集合」のことです。例えば、自然数の集合 $`{\bf N}`$ を名前の集合に選んでもかまいません。

世界 $`\wrld{W}`$ と名前の集合 $`\mrm{Name}`$ が決まっている状況で、名前への値割り当て〈value assignment〉、あるいは付値〈valuation〉とは、次のような写像 $`v`$ です。

$`\quad v:D \to \mrm{Thing}\, \wrld{W}\\
\quad \text{where } D \subseteq \mrm{Name}`$

例えば、名前の集合に英字の文字列が含まれるとして、$`D := \{\text{"one"}\}`$ として、集合 $`D`$ 上で定義された付値 $`v`$ を定めましょう。文字列 $`\text{"one"}`$ は、自然数の 1 を意味するとします。

世界 $`\wrld{W}`$ の銀河の集合 $`\mrm{Galx} = \wrld{W}_\mrm{Galx}`$ には通常の集合圏 $`{\bf Set}`$ は含まれます。したがって、自然数の集合 $`{\bf N}`$ も銀河の対象として存在します。1 は集合 $`{\bf N}`$ の要素ですが、圏論的パス式では要素にアドレスできないので、次の射〈写像〉を考えます。

$`\quad 1^\sim : {\bf 1} = \{*\} \to {\bf N} \In {\bf Set}\\
\quad {\bf 1} \ni * \mapsto 1 \in {\bf N}
`$

付値 $`v`$ の唯一の値は、圏論的パスを用いて次のように定義されます。

$`\quad v: \{\text{"one"}\} \to \mrm{Thing}\,\wrld{W}\\
\quad v(\text{"one"}) := \Path{\bf Set}/({\bf 1}, {\bf N})/1^\sim`$

文法と付値の拡張

「名前」というと、名詞を連想するかも知れませんが、名前の集合とは「任意の可算無限集合」のことだったので、その要素が名詞かどうかは意味がありません。しかし、品詞に相当する概念を入れて、名前の集合を分割してもかまいません。あるいは、幾つかの名前の集合を寄せ集めて名前全体の集合を作ってもかまいません。

名前はアトミックな構文的対象物ですが、文法により複雑な構文的対象物を組み立てることができます。例えば、数値の名前〈数詞〉と演算の名前〈演算子記号〉から、適切な文法規則で算術式を組み立てることができます。変数の名前〈変数名〉も入れれば、変数を含んだ算術式、例えば2x + y^2 + 5が構成できます。

文法により構成された複雑な（複雑かも知れない）記号的表現＝構文的対象物を項〈term〉とか式〈expression〉と呼びます。

項を構成する名前に付値があれば、項全体まで付値を拡張できます。その拡張手段を与えるのが構文論と意味論です。例えば、先の算術式2x + y^2 + 5に出現するすべての名前〈記号 | ラベル〉を列挙して付値を与えましょう。

名前 値〈意味〉
2 自然数の 2
省略されている演算子記号 自然数の掛け算
x 自然数の 1 とする
+ 自然数の足し算
y 自然数の 2 とする
^ 自然数の累乗
5 自然数の 5

上の表で与えられた付値を $`v`$ として、拡張された付値を $`V`$ とすると、項の値〈意味〉は次のように計算されます。

$`\newcommand{\op}[1]{(#1)_{\bf N}}
\newcommand{\lit}[1]{ {#1} }
\quad V(\text{'2x + y^2 + 5'}) \\
= v(\text{'+'})(\,
v(\text{'+'})(\, V(\text{'2x'}),\, V(\text{'y^2'})\, ),\, v(\text{'5'}) \,)\\
= v(\text{'+'})(\,
v(\text{'+'})(\, v(\text{'*'})(\, v(\text{'2'}),\, v(\text{'x'}) \,),\,
v(\text{'^'})(\, v(\text{'y'}),\, v(\text{'2'}\,) \,)
),\; v(\text{'5'})
\,)\\
= \op{+}(\,
\op{+}(\,
\op{*}(\, \lit{2},\, v(\text{'x'})
\,)
,\,
\op{\text{^}}(\,
v(\text{'y'}),\, \lit{2}
\,)
\,)
,\;
\lit{5}
\,)\\
= \op{+}(\,
\op{+}(\,
\op{*}(\, \lit{2},\, \lit{1}
\,)
,\,
\op{\text{^}}(\,
\lit{2},\, \lit{2}
\,)
\,)
,\;
\lit{5}
\,)\\
= 11
`$

簡単な自然数の算術計算をしちめんどくさく書いているわけですが、これは、我々が無意識に頭のなかで行っていることを明示的に書き出したものです。

意味論の習慣では、基本となる付値 $`v`$ をもとに拡張された付値を $`\BR{\text{2x + y^2 + 5}}_v`$ のように書きます。括弧記号 $`\BR{\hyp}`$ はスコットブラケット〈Scott brackets | denotation brackets | semantic brackets | Oxford brackets〉と呼ばれます。

構文論と意味論がやるべきことは、語彙と文法を決めて、その文法に沿って付値をどのように拡張するかを決めることです。つまり、スコットブラケットをキチンと定義することです。

構文論と意味論を語る困難

「語彙と文法を決めて、その文法に沿って付値をどのように拡張するかを決める」ことはときに随分と複雑になります。その複雑性は「それはそんなもんだ」と受け入れるにしても、構文論と意味論を語ることには常に困難が付きまといます。それは、使われている名前・語・式などが、どの言語に属するものかを明示するのが極めて煩雑なことです。かといって、へたに省略すると、読む側／聞く側は混乱します。塩梅が難しいですね。

構文論と意味論を語る道具である言語達を図示すると次のようになるでしょう*2。

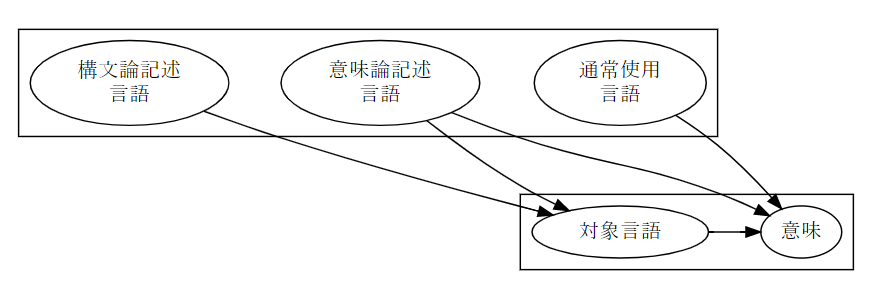
下側の「対象言語」は語る道具ではなくて、語られる対象です。上側の3つの言語は通常の意味での言語ですが、対象言語〈オブジェクト・レベルの言語〉との比較においてはメタ言語ということになります。

上側右の「通常使用言語」とは、自然言語〈日本語〉と数学的記法を混ぜた、地の文で使う言語です。この「通常使用言語」を使って意味的対象物（下側の右）を語ります。上側左の「構文記述言語」は、BNF記法（「コンピュータによる言語処理の常識」参照）のように、構文を記述するための専用の言語です。上側中央は、構文と意味の関係を記述する言語で、スコットブラケットはこの言語に属する記号です。

異なる言語に属する記号が、オーバーロードされたり同一視されたりします。それは、常に混乱のリスクを伴います。例えば、次は本来区别すべき記号の例です。

  • 自然数の 5 を参照〈denote〉する通常使用言語の記号「5」と、対象言語の記号「5」
  • 対象言語の変数名「x」と、対象言語の変数名の集合を変域とする構文記述言語の変数名「x」
  • 型の実体である銀河の対象「$`A`$」と、対象言語の型リテラルである「A」

スコットブラケットの定義や計算は、しばしば同語反復のように見えることがあります。

$`\quad \BR{3 + 1} = \BR{3}\BR{+}\BR{1} = 3 + 1`$

この例で、スコットブラケットの内側の数詞や演算子記号は対象言語の構文的対象物で、スコットブラケットの外に出た数詞や演算子記号は通常使用言語（地の文）のものです。地の文の表現により、意味的対象物である自然数や演算を参照します。

型項（型を表す記号的表現）の意味論では、例えば次のような定義が現れるかも知れません。

$`\quad \BR{A \times B} := \BR{A} \times \BR{B}\\
\quad \BR{A \to B} := [\BR{A}, \BR{B}]
`$

上の定義の左辺の「$`\times`$」は対象言語の記号で、右辺の「$`\times`$」は通常使用言語、または意味論記述言語に属する記号です。下側左辺の矢印は対象言語の記号で、下側右辺の（スコットブラケットではない）ブラケットは通常使用言語、または意味論記述言語に属する記号です。通常使用言語では、矢印記号は別な意味で使われでしょう（「矢印記号の憂鬱」参照）。

このテの困難は原理的にどうしようもないので、書く側／読む側がお互いに注意してコミュニケーションに努めるしかありませんね。

*1:インデキシング $`\cat{G}:I \to \mrm{Galx}`$ を固定して、集合 $`I`$ の側に順序が入っているとしてもかまいません。

*2:この絵の構造全体を語る言語として、再び「通常使用言語」が使われます。