以前にここで提出したアミダのクイズをErlangプログラムにより解いてみました。「解いた」とは言っても、プログラムが解の候補を全部列挙するシラミツブシ方式ですけどね。でも、これで遊んだり実験してみると、なかなか楽しいですよ。
内容:
●アミダのクイズとは
以前のエントリー「アミダのクイズ」(いま読み返さなくてもいいです)に書いたものです。ごく少数の方は興味を持ってくれたみたいです。
コメント欄から:
タナカコウイチロウ
こんにちは。
なんか、差し出がましいのですが、Lightweight Languageイベントの「「キミならどう書く」お題募集」に良いのではないでしょうか?
m-hiyama
タナカコウイチロウさん、
実験をするプログラムはいろいろと書きようがあるでしょうが、実はこれ、チャントした正解はわからないんですよ(苦笑)。
「重さが最小のアミダ図は、横棒の数も最小である」が示せれば、割とハッキリするのですが、今のところ、“たぶんそうに違いない”と思っているだけでして。suroyuu
檜山さん、僕も考えてみたのですが正解が分かりません。いつの日か正解が公開される事を楽しみにしてます。
予備知識としては、「はじめての圏論 第7歩:アミダの圏」が必要です。圏論と直接の関係はないので、2番目の節「アミダ」だけ読めばOKです。アミダ図が整数の列(リスト)で表現できることを確実に押さえてください。例えば次のアミダ図は、[1, 2, 2, 1]と[1, 2, 1, 3, 2, 1, 3]で表現されますね。
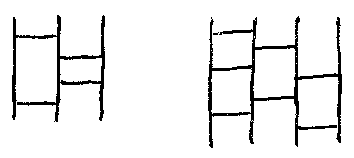
アミダ図を整数列で表現した場合の、整数達の総和をアミダ図の重さと呼びます。上の例では、それぞれ重さ 1 + 2 + 2 + 1 = 5、1 + 2 + 1 + 3 + 2 + 1+ 3 = 13 です。与えられたアミダ図と同じ効果を持ち(アミダクジとして同じ結果を出すもので)、重さが最小のアミダ図を求めよ -- これが“アミダのクイズ”です。(もっと直観的な説明は「アミダのクイズ」を参照。)
●なぜErlangを使うのか
「習いたてで使ってみたい」てのが実は主たる理由です(「僕もErlangを試してみたよ -- 軽量プロセスを中心に」参照)。「無理矢理にでも軽量プロセスを使ってやるぞ」とプログラムを書き始めたのですが、出来上がってみると、この問題は本来Erlang軽量プロセス向きだった気がします。
Erlangの言語仕様に慣れてなくてハマったところもありますが、他の言語(例えばJava)で書くことを考えてみれば、Erlangで軽量プロセスを使う方法は格段に楽だと言えます。以下がソースコードです。
次のように使います。
Erlang (BEAM) emulator version 5.5.4 [async-threads:0]Eshell V5.5.4 (abort with ^G)
1> c(amida).
{ok,amida}
2> amida:solve([1, 2, 2, 1]).<0.37.0>
===><0.39.0>: [start,[1,2,2,1]] 6
===><0.40.0>: [start,[1,2,2,1],cntr,[1,1]] 2
===><0.41.0>: [start,[1,2,2,1],cntr,[1,1],cntr,[]] 0
3>
amida:solve(アミダ図を表すリスト).とするとアミダのクイズを解きます。詳細はともかくとして、[1, 2, 2, 1]と同じ効果を持つ(以下では、「[1, 2, 2, 1]と同値な」と表現します)アミダ図は、それ自身を含めて3つ:
- 重さ6 [1,2,2,1]
- 重さ2 [1,1]
- 重さ0 []
であることがわかります。(リストの長さが増える[1,2,2,1,2,2]などは考えません。)なお、このプログラムは手抜きなので、注意事項をいくつか。
- 生成したプロセスを管理してないので、プログラムの終了を判断してません(できません)。待ち状態のプロセスが残るので、必要なら手作業で始末してください。
- 得られた結果を整理整頓はせず、プロセス達の作業結果を出来た順で表示しているだけです。
これらは問題点ですが、いかにも並行プロセスでやってるって感じがしますよね(って、半分言い訳)。
([追記]ンギョッ、「アミダのクイズ」では、「同値」じゃなくて「合同」と言っていたんだ。ウーン、用語法が食い違っているけど、似た言葉だから、まーいいとしよう。[/追記])
●実験してみよう
先に図を出しておいたもう1つの例[1,2,1,3,2,1,3]をやってみます。
解の候補がイッパイあるようです。変数Pに代入しておいたプロセスに結果が蓄積されているので表示させてみます(print_data関数を使う)。
3> P = amida:solve([1,2,1,3,2,1,3]).<0.42.0>
===><0.44.0>: [start,[1,2,1,3,2,1,3]] 13
===><0.45.0>: [start,[1,2,1,3,2,1,3],flip,[2,1,2,3,2,1,3]] 14
………………………………
…… 省略 ……
………………………………
===><0.154.0>: [start,[1,2,1,3,2,1,3],ichg,[1,2,3,1,2,1,3],flip,[1,2,3,2,1,2,3]
flip,[1,3,2,3,1,2,3],ichg,[3,1,2,3,1,2,3],ichg,[3,1,2,1,3,2,3],flip,[3,1,2,1,2,
,2],flip,[3,1,1,2,1,3,2],ichg,[3,1,1,2,3,1,2]] 13
4>
4> amida:print_data(P).
1 [3,2,1,3,2,3,3] 17 2
2 [3,2,3,1,2,3,3] 17 2
………………………………
…… 省略 ……
………………………………
39 [2,3,1,2,1] 9 5
40 [2,1,3,2,1] 9 5
ok
5>
[1,2,1,3,2,1,3]と同値なアミダ図は40種類あるようです。もとのアミダ図の重さは13ですが、同値なアミダ図の重さは、17から9の範囲に分布してます。[3,2,1,3,2,3,3]と[3,2,3,1,2,3,3]が重さ17で、[2,1,3,2,1]と[2,3,1,2,1]が重さ9です。この例では、17から9のあいだのすべての整数が重さになっています。適当に拾ってみると:
- 重さ17 [3,2,1,3,2,3,3]など
- 重さ16 [3,2,1,2,3,2,3]など
- 重さ15 [3,1,2,1,3,2,3]など
- 重さ14 [2,1,2,3,2,3,1]など
- 重さ13 [1,2,1,3,2,1,3]など
- 重さ12 [1,2,1,2,3,2,1]など
- 重さ11 [3,2,3,1,2]など
- 重さ10 [2,3,2,1,2]など
- 重さ09 [2,3,1,2,1]など
この9個に関しては実際に絵を描いて同値であることを確認しました。ゴクローサン>俺
結局、[1,2,1,3,2,1,3](重さ13)と同値なアミダ図で重さが最小なアミダ図は:
- [2,3,1,2,1](重さ9)
- [2,1,3,2,1](重さ9)
の2つ、という結果が得られました。
※ ここから先、プログラムの仕掛けをばらします。アミダのクイズにチェレンジしたい方は、読むのを中止してください :-)
●アルゴリズムの背景:アルチン変形
プログラムamida.erlで採用した方法を説明しましょう。基盤となるのは、アルチン(Emil Artin)によるブレイドに関する定理をアミダに適用したものです*1。理屈の説明は別な機会にして、必要な手順だけ述べます。
まず、アミダ図の一部に注目して次の3種の変形を考えます。
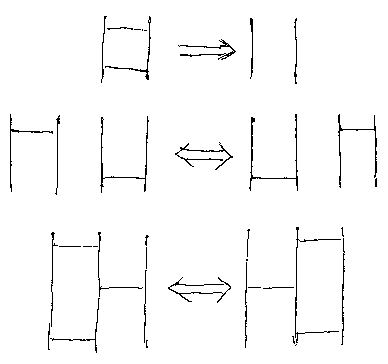
これらの変形を、上から順に縮約(contraction)、交換(interchange)、フリップ(flip)と呼びます(ここだけの呼び名)。
縮約は逆方向に行うこともできますが、横棒の数を増やしてもしょうがないので、横棒を減らす方向だけを考えます*2。交換とフリップは双方向なので、方向を区別すると全部で5種類の変形になります。これらを総称してアルチン変形と呼びましょう。
([追記]「アルチン変形」の意味が、ひとつの変形か、いくつかの変形の列か混乱気味だったので修正しました。[/追記])アルチン変形を行っても、アミダ図の効果(アミダクジとしての働き)は変わりません(目視で容易に確認できますね)。つまり、アミダ図Aからアミダ図Bが何回かのアルチン変形により得られたとき、AとBは同値です。
- A→Bというアルチン変形の列がある ならば AとBは同値
ですね。問題はこの逆の命題ですが、アルチンにより次が証明されています。
- AとBは同値 ならば A→Bというアルチン変形の列がある
あるいは対偶を取って:
- A→Bというアルチン変形の列がない ならば AとBは同値ではない
これから、与えられたアミダ図Aに、可能なアルチン変形をどんどん適用していけば、Aと同値な(ただし、横棒は増えない)アミダ図をすべて見つけられることが保証されます。だから、もれなく次々とアルチン変形を実行するプログラムを作ればいいわけです。
●アルチン変形をもう少し具体的に
アミダ図は整数の列(リスト)で表現できるので、アルチン変形は整数リストへの操作としてプログラミングできます。次のようになります。
- 縮約:[…, n, n, …] → […, …]
- 交換1:[…, n, m, …] → […, m, n, …](n < m、m - n ≧2)
- 交換2:[…, m, n, …] → […, n, m, …](n < m、m - n ≧2)
- フリップ1:[…, n, n+1, n, …] → […, n+1, n, n+1, …]
- フリップ2:[…, n+1, n, n+1, …] → […, n, n+1, n, …]
交換できるのは、nとmの差が2以上のときだけです。m = n なら縮約を適用するし、m = n + 1 での交換は同値性を壊してしまいます(下図)。
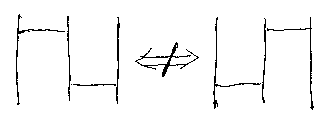
表にまとめておきましょう。上の箇条書きと少し表現を変えてあるのは、amida.erlに合わせるためです。amida.erlは下の表に従ってコーディングされています。
| 変形名称 | 適用条件 | 変形パターン |
|---|---|---|
| 縮約 | n = m | n, m → (何もなし) |
| 交換1 | n < m - 1 | n, m → m, n |
| 交換2 | n > m + 1 | n, m → m, n |
| フリップ1 | n = l and m = n + 1 | n, m, l → m, n, m |
| フリップ2 | n = l and m = n - 1 | n, m, l → m, n, m |
交換とフリップは双方向変形なので、素朴にプログラムを書くと容易に無限ループします。無限ループを避けるために、確認済みのデータ(整数リスト)を記録しておき、重複実行をチェックするしかないでしょう。amida.erlでは、アルチン変形を複数のワーカー・プロセスに並列実行させて、マネージャ・プロセス*3が確認済みのデータを蓄積するようにしています。amida.erlにはコメントをたくさん入れておいたので、Erlang構文に不慣れな方でも何をやっているかは読み取れるでしょう。
●アミダのクイズはまだ解けていない
もともと僕が「アミダのクイズ」において期待していた解法はシラミツブシ法ではありません。シラミツブシより効率的な方法が欲しいのです。
現状で分かっていること/分からないことは:
- 与えられたアミダ図と同値で横棒が最小であるアミダ図は、割と効率的に求められる。
- 同値類の中で、重さ最小のアミダ図は横棒数(リストの長さ)も最小だろうと信じているが、確証はない。
- もう少し一般的に述べると、アミダ図の同値類において、n≦m かつ最小値が定義できる前提で、(横棒数nにおける重さの最小値)≦(横棒数mにおける重さの最小値)*4。これが成立してないと、「横棒数が増える変形は無視する」ことも合理化できない。
- もし「重さ最小なら横棒数も最小」なら、交換とフリップだけを適用したシラミツブシを適用できる。
- 交換とフリップを適用するにしても、効率的な戦略があるのかもしれない。
シラミツブシ法であっても、Erlangよりもっとポピュラーな言語で実装するとか、使い勝手をよくするとか、やることはあります(僕はやる気ないけど)。ちなみに、これは単なるクイズで終わるわけではなくて、図式的変形(geometric simplification (c)Abramsky)を組み合わせ計算(combinatorial calculation)で実行する事例となっています。
*1:アミダ(正式に言えば対称群)に関するアルチンの定理に相当する結果は、別な人の名前で呼ばれています。が、それが誰だか思いだせません→http://d.hatena.ne.jp/m-hiyama-memo/20070523/1179878286
*2:横棒が増える変形を考えなくていいかどうかは自明ではありません。このエントリーの最後の節を参照。
*3:マネージャつっても、ちっともワーカー達をマネージしてねーけどね。
*4:横棒の本数を変えるアルチン変形は縮約だけなので、nとmの差は2の倍数になります。