平面タングル、空間タングル、ブレイドなんかが“もつれた”話

「単純平面タングルとカウフマン図のキャンバス・基準点について」において、平面タングルに触れました。平面タングルを空間タングルに一般化して、その後で特殊化することでブレイドが出てきます。結び目や絡み目もタングルの特殊なものとして出現しますが、それらの相互関係はけっこうややこしいです -- 絡み合い、もつれ合っています。

内容：

平面タングルとその変種
空間タングルとその変種
方体タングル
ブレイド
タングルの定義
幾何タングル
結び目、絡み目、ブレイド
方体タングルのモノイド圏
記号的モノイド圏
組み合わせブレイド
タングルの圏の公理的な特徴付け
もつれを整理すると

平面タングルとその変種

平面タングル（planar tangle）は、穴あき円板をキャンバス（描画領域）にして、その上に紐（ワイヤー、糸、ロープなど）で模様を描いたものです。「単純平面タングルとカウフマン図のキャンバス・基準点について」では、平面タングルの特殊なものとして円環タングル（annular tangle）と、キャンバスが矩形となる矩形タングル（rectangular tangle）も紹介しました。

（一般的な）平面タングル、円環タングル、矩形タングルの三者について表にまとめましょう。

タングルの種類	キャンバス	入口境界	出口境界
平面タングル	穴あき円板	幾つかの円	ひとつの円
円環タングル	円環	ひとつの円	ひとつの円
矩形タングル	矩形	線分	線分

キャンバスは2次元の領域です。キャバスの境界の一部が入口境界（incomming boundary）と出口境界（outgoing boundary）になっています。入口境界と出口境界上に点（ドット）が乗っていて、それらの点が紐の両端になります。

キャンバス上に描かれた紐模様が圏の射となります。圏の対象は、ドットの集合です。入口境界上のドットの集合が射の域、出口境界上のドットの集合が射の余域となります。ドットに個性はないので、ドットの個数を指定すればドットの集合を記述できます。そのため、圏の対象は自然数（0, 1, 2, ...）と同一視します。

空間タングルとその変種

平面タングルのキャンバスを2次元から3次元へと一般化します。空間領域をキャンバスとします。ここで「空間」は、我々が棲んでいる3次元空間のことです。

タングルの種類	キャンバス	入口境界	出口境界
空間タングル	穴あき球体	幾つかの球面	ひとつの球面
球殻タングル	球殻	ひとつの球面	ひとつの球面
方体タングル	方体（直方体）	矩形	矩形

「平面→空間（3次元）」という一般化にともない、「円板→球体」、「円（周）→球面」、「矩形→方体」、「線分→矩形」のような一般化をしています。球殻は、球体から内部の球体を抜いた形、アンコを取り去ったおまんじゅうのような形です。入口境界と出口境界の面上にいくつかのドットを打ち、紐はドットとドットを結ぶように配置します。全般に次元が1上がります。

紐は交差したり分岐したり切れたりしませんが、3次元なので絡み合う／もつれ合うことができます。事情は非常に複雑になります。上の3種のタングルのなかでは、方体タングル（cubical tangle）が一番扱いやすいでしょう。以下、方体タングルに注目することにします。

方体タングル

方体タングルのキャンバス領域は、3次元の方体（直方体）なので、箱とか部屋にたとえることができます。入口境界が天井で、出口境界が床と考えましょう。紐の端になるドットは、直線上に配置されていることにします。

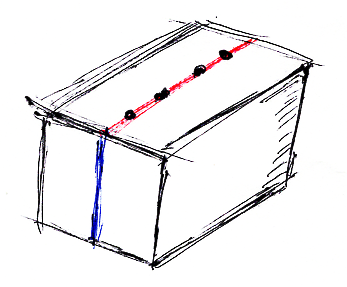
上の絵で、赤はドットが並ぶ直線（線分）で、4個のドットが並んでいます。ドットからドットへと向かう紐は、部屋の内部を通ります。紐の様子は次のような図で描けるでしょう。結び目図（knot diagram）と同じ要領で、交差部分で奥行きが分かるように描きます。

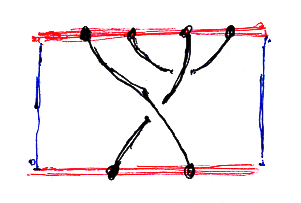
方体タングルでも、複雑な絡み合い／もつれ合いは生じます。

絡み合い／もつれ合いは難しいですね。

ブレイド

方体タングルでは、天井から天井、床から床への紐を認めています。このような紐がつながると、天井にも床にも壁にも触らないで、部屋の内部で閉じる紐ができます -- 結び目（knot）ですね。単一の結び目に限らず、複数の結び目がさらに絡み合う状況も生じます -- 絡み目（link）ですね。

事情を単純にするために、天井から床に向かう紐しか認めないことにします。このように制限した方体タングルはブレイド（braid; 組み紐）になります。ブレイドについては次の記事に書いてあります。

はじめての圏論中間付録B：アミダとブレイド

ブレイドを平面に投影して、2種の交差が区別できるように描いた図をブレイド図（braid diagram）と呼ぶことにします。ブレイド図の全体は圏をなします。ブレイド図の圏に関しては、次を参照してください。

2つの結び目図（結び目の射影図）が同じ結び目を表すのは、ライデマイスター移動（Reidemeister moves）で互いに移れるときです。同様に、ライデマイスター移動で互いに移れる2つのブレイド図は同じブレイドを表します。このとき使うライデマイスター移動は、II番とIII番だけで、ライデマイスター移動I番は使いません。（以下の図の左と右を入れ替えるのがライデマイスター移動。まん中は移動の中間状態。）

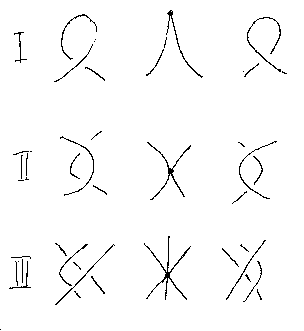
ブレイドの同値性を定義するにはもう少し精密な議論が必要ですが、後でまたブレイドの話題に触れます。

タングルの定義

今まで、タングルやブレイドという言葉を正確には定義していませんでした。キッチリ議論するなら、例えば「タングル」という言葉の4種の意味を区別すべきです。

幾何タングルのインスタンス：幾何的に定義された個々の図形（のパラメータ表示）
幾何タングルのクラス：幾何的に定義された個々の図形の同値類
組み合わせタングルのインスタンス：組み合わせ的に定義された語（記号の組み合わせ）
組み合わせタングルのクラス：組み合わせ的に定義された語の同値類

方体タングルに関して、幾何的な定義をしてみましょう。定義の舞台となる圏の選び方が色々ありますが、ここでは位相多様体と連続写像の圏で考えることにします。図形はこの圏の対象 -- つまり位相多様体だけを考えます。

I = {x∈R | 0≦ x ≦1} とします。I³ = I×I×I を（標準的な）方体とします。z軸が鉛直方向（重力方向）下から上に向かうとみなして、床の線分H₀と天井の線分H₁を定義しておきます。

H₀ = {(x, 1/2, 0)∈I³ | 0＜ x ＜1 }
H₁ = {(x, 1/2, 1)∈I³ | 0＜ x ＜1 }

床の中央線H₀の代わりに床全体、天井の中央線H₁の代わりに天井全体でもいいのですが、線分H₀, H₁を定義しておくと若干話が簡単になります。例えば、線分上に乗る有限個の点には全順序を付けることができます。

さて、Xを1次元コンパクト（位相）多様体とします。1次元（境界を許す）コンパクト多様体は線分と円周の有限直和です。円周をS¹と書くなら：

X $\stackrel{\sim}{=}$ I + ... + I + S¹ + ... + S¹

と書けます。線分Iの個数をn、円周S¹の個数をmとして、次のように書くことにします。

X $\stackrel{\sim}{=}$ nI + mS¹

3I + 2S¹ = (｜ ｜ ｜ ○ ○)

同相な図形は同一視してしまう、あるいは同相な類から代表を1つだけピックアップすると考えれば、

X = nI + mS¹

としてもかまいません。

幾何タングルのインスタンス（geometric tangle instance）は、α:X→I³ という連続写像で、次の条件を満たすものです。X^○はXの内部、∂XはXの境界です。

αは埋め込みである。Xと像α(X)は同相な多様体。
α(X^○) ⊆ (I³)^○
α(∂X) ⊆ (H₀∪H₁)

2番目の条件は、紐の両端以外の部分は、部屋の天井・床・壁に接触しないことを表しています。仮に接触しても、少し紐を動かせば部屋の内部に収まりますが、最初からこの条件を付けておくことにします。

3番目の条件は、紐の両端は天井と床の中心線（H₀とH₁）に乗ることを表しています。X = nI + mS¹ だったので、∂Xは2n個の点からなります。k₀ + k₁ = n + m となる2つの整数k₀, k₁があり、次の状況となります。

α(∂X)のうちk₀個の点がH₀内にあり、k₁個の点がH₁内にある。

今定義した幾何タングルのひとつひとつのインスタンスを別々なものとみなすのではなくて、似たものは「同じ」とみなします。「同じ」とみなす基準を次節で述べます。

幾何タングル

α:X→I³, β:Y→I³ を2つの幾何タングルのインスタンスとして、XとYが τ:X→Y で同相であり、α = τ;β のとき、αとβは「同じ」とみなします。αとβがこの意味で「同じ」とき、α(X)とβ(Y)はI³の部分多様体として同じになります。αとβは、描いた図形の形状（＝点集合）は同じでパラメータ表示方法（＝動作としての描きっぷり）の差があるだけです。

描かれた図形をグニグニ動かしてもいいということを表すためには、アンビエント・イソトピーを使います。Φ:[0, 1]×I³→I³ という連続写像があるとき、φ_t(p) := Φ(t, p) と書くことにします。

2つの幾何タングルのインスタンス α, β:X→I³ に対して、Φ:[0, 1]×I³→I³ が、αからβへのアンビエント・イソトピー（ambient isotopy）だとは：

tがなんであっても、φ_t:I³→I³ は同相写像である。
tがなんであっても、φ_t(H₀) = H₀ で、φ_tをH₀に制限したものはH₀の同相写像となる*2。
H₁に関しても前項と同様。
φ₀ はI³の恒等写像。
φ₁ $\circ$ α = β （' $\circ$ 'は反図式順結合の記号）

αからβへのアンビエント・イソトピーΦがあるとき、αとβはアンビエント・イソトピック（ambient isotopic）と呼びます。1次元コンパクト多様体Xを固定すると、Xからの幾何タングル・インスタンスの全体にはアンビエント・イソトピックによる同値関係が入ります。

「パラメータ表示の違いしかないなら同じ」と「アンビエント・イソトピックなら同じ」という2つの同値関係を組み合わせた同値関係を考えて、これを幾何タングルのインスタンスのあいだの同値関係とします。

幾何タングルのインスタンス全体に今述べた同値関係を入れて、その同値類を幾何タングルのクラス（geometric tangle class）と呼びます。単に幾何タングルと言ったときは、幾何タングルのクラスのことです。あるいは、クラスの代表としてのインスタンスのことです。個々のインスタンスを別物として扱うことはありません。

ここまでの定義では、幾何タングルのインスタンスとクラスを区別しましたが、実際に区別されることはほとんどなくて、文脈により適宜解釈を変えます。

結び目、絡み目、ブレイド

αは幾何タングル（クラスの代表となるインスタンス）とします。αの定義域は X $\stackrel{\sim}{=}$ nI + mS¹ だとします。ここで、n, mは任意の自然数で、nが線分（閉区間）の個数、mが円周の個数です。Xの位相同型類は自然数n, mで完全に決まります。

n = (線分の個数), m = (円周の個数) に対して制限を付けます。すると、タングルの特殊ケースが定義できることになります。

n = 0, m = 1 ：ただひとつの円周S¹から方体I³への写像で定義されるタングル。
n = 0, m = m （制限なし）： m個の円周mS¹から方体I³への写像で定義されるタングル。
n = n （制限なし）, m = 0 ： n個の線分nIから方体I³への写像で定義されるタングル、ただし、天井から床に向かう紐しか認めない。

上記の特殊なタングルには名前が付いていて、次のように呼びます。

結び目（knot）
絡み目（link）
ブレイド（braid）

ブレイドだけを相手にしたいときは、パラメータ表示 β:nI→I³ をもっと制限して考えたほうが便利です。例えば：

紐の境界の点を (i/(n + 1), 1/2, 1), (i/(n + 1), 1/2, 0) （i = 1, 2, ..., n）に限定する。
βを β(i, t) （i = 1, ..., n, 0≦ t ≦1）の形に書くとして、π₃はz方向への射影として、iがなんであっても π₃(β(i, t)) = t。

こうすると、tを時間パラメータと考えて、ブレイドに対する次の描像が生まれます。

初めは直線状にキチンと整列していたn個の点が、2次元矩形内で互いに接触せずに動き回り、最後はまたキチンと整列する。ただし、各点がもとの位置に戻るとは限らず、入れ替わるかも知れない。

方体タングルのモノイド圏

平面の一部に描かれる円環タングルや矩形タングルは、キャンバスの貼り合わせとサイズ調整（リスケーリング）により圏になりました。矩形タングルの場合は、左右に並べて貼り合わせることによりモノイド積が定義できて、モノイド圏となるのでした。

方体タングル（クラス）の全体もモノイド圏になります。モノイド圏の構造を与える方法は矩形タングルのときと同じです。

圏の対象はドットの集合だが、自然数と同一視する。
圏の射は方体タングル（のクラス）
射の域（domain）は天井に並ぶ紐の境界であるドット（結合方向が上から下とする）
射の余域（codomain）は床に並ぶ紐の境界であるドット（結合方向が上から下とする）
射の結合は、キャンバス方体を縦にくっつけて位置とサイズを調整する。紐もちゃんと繋ぐ。
対象のモノイド積は自然数の足し算、射のモノイド積はキャンバス方体を横に並べて位置とサイズを調整する。

こうして方体タングルの全体は圏となります。結び目、絡み目、ブレイド達は、方体タングルの圏の部分圏を形成します。しかし、結び目の圏と絡み目の圏は対象が1つ（0だけ）しかなく、モノイド積と結合が一致してしまい、モノイド圏と考えてもあまり嬉しくないです。でもブレイドの圏は、モノイド圏として考えることに意味があります。

記号的モノイド圏

幾何タングルは図形的な存在なので、絵に描けるし幾何的直感で扱うこともできます。しかし、記号計算の対象にはなりません。これでは不便なので、記号的な計算体系が欲しくなります。

記号的な計算体系を作るには次のようにします。

有限個の基本記号を準備する。
基本記号を組み合わせて記号列（複合記号）を作る規則を決める。
2つの記号列が「同じ」と判定する規則を決める。

記号列のことを語（word）と呼びます。基本記号から語を作る規則（文法）は次のようなものです。

空列()は語である。()を空語とも呼ぶ。
基本記号は語である。
AとBが語のとき、(A*B)は語である。
AとBが語のとき、(A,B)は語である。
以上により定義されたものだけが語である。

この規則のなかで使われた丸括弧、星印、カンマは、基本記号（ユーザー指定記号）とは別に最初から準備されているシステム組み込み記号です。a, bが基本記号だとすると、次のような語を作れます。

()
b
(a*b)
((a*b);())
(((a*b);())*(b;b;()))

この定義だと圏論的議論には適さないので、もう少し構造を追加します。基本記号の集合Σに、src, trg:Σ→N という写像を付けます。語に対しても src, trg を拡張しながら語を再定義します。

空列()は語である。src(()) = 0, trg(()) = 0 。
自然数nは語である。src(n) = n, trg(n) = n 。
基本記号xは語である。src(x), trg(x) は、x∈Σ なので最初から定義されている。
AとBが語のとき、(A*B)は語である。src((A*B)) = src(A) + src(B), trg((A*B)) = trg(A) + trg(B) 。
AとBが語で、trg(A) = src(B) のとき、(A,B)は語である。src((A,B)) = src(A), trg((A,B)) = trg(B) 。
以上により定義されたものだけが語である。

以上のようにして定義した語の集合をWord(Σ)とします。src, trg:Σ→N を拡張した写像 src, trg:Word(Σ)→N があり、埋め込み inj:Σ→Word(Σ) もあります。Word(Σ)に適当な同値関係を入れると、Nを対象とするモノイド圏ができます。このモノイド圏はPRO（「PROと代数系 -- toward 量子と古典の物理と幾何＠名古屋』参照）なので、PRO(Σ)と書くことにします。

PRO(Σ) = (N, Word(Σ)/〜, dom, cod, id, ;, $\otimes$ ) として、語Aの同値類を[A]と書くなら：

dom([A]) = src(A)
cod([A]) = trg(A)
id_n = [n]
[A];[B] = [(A,B)]
[A] $\otimes$ [B] = [(A*B)]

Word(Σ)上の同値関係が煩雑で退屈なので省略しましたが、PRO(Σ)は、我々が厳密モノイド圏に対して行う計算を形式化した記号的体系になっており、それ自身が厳密モノイド圏です。

組み合わせブレイド

自然数を対象、幾何ブレイド（クラス）を射とするモノイド圏をBraidとします。自然数（Braidの対象）nに対してエンドセットBraid(n, n)を考えると、これは圏の結合を演算として群になります。これを、n-紐のブレイド群（braid group on n-strands）、あるいはn-ブレイド群と呼びます。

n-ブレイド群は、群の生成系（system of generators）と関係系（system of relations）による表示（presentation）を持ちます。(n - 1)個の生成元 σ₁, σ₂, ..., σ_n−1 から生成された自由群を考えて、そのなかで次の関係を導入します。

|i - j| ≧ 2 のとき、 σ_iσ_j = σ_jσ_i （i, j∈{1, ..., n - 1}）
σ_iσ_i+1σ_i = σ_i+1σ_iσ_i+1 （i∈{1, ..., n - 2}）

生成系と関係系で定義した群は組み合わせブレイド群（combinatorial braid group）または代数ブレイド群（algebraic braid group）と呼びましょう。組み合わせブレイド群の要素は、σ₁, σ₂, ..., σ_n−1 という(n - 1)個の記号とその逆σ_i^-1を何個か（重複を許す）選んで並べたもの（これをブレイド語と呼ぶ）です。ただし、逆元の性質と上記の関係で同値なものは同一視します。

幾何ブレイド群と組み合わせブレイド群は同型です。この事実はアルチン（Emil Artin）により示されました*3（アルチンの定理）。上記の関係式はアルチン関係（Artin relations）と呼ばれます。2番目のアルチン関係は、幾何ブレイドのライデマイスター移動III番に対応します。

ブレイド群はブレイドの圏のエンドセットを取り出したものです。ブレイドの圏全体を組み合わせ的に（生成系と関係系により）定義できないでしょうか。これはアルチンの定理とほぼ同じように示せます。

Σ = {b, b'} を基本記号の集合とする。
src(b) = trg(b) = 2, src(b') = trg(b') = 2 とする。
基本記号の集合Σから厳密モノイド圏PRO(Σ)を作る。
PRO(Σ)にアルチン関係と同様な関係を入れる。

PRO(Σ)に入れる関係は：

(b,b') = (b',b) = 2 （bとb'は互いに逆）
((b*1),(1*b),(b*1)) = ((1*b),(b*1),(1*b)) （ライデマイスター移動III）

圏論の標準記法でもっと分かりやすく書けば：

b;b' = b';b = id₂
(b $\otimes$ id₁);(id₁ $\otimes$ b);(b $\otimes$ id₁) = (id₁ $\otimes$ b);(b $\otimes$ id₁);(id₁ $\otimes$ b)

“幾何ブレイドの圏”と“組み合わせブレイドの圏”を区別しないのは、アルチンの定理の圏論版*4があるからです。つまり、次が成立します。

幾何ブレイドの圏と組み合わせブレイドの圏のあいだには、対象類（N）上で恒等で可逆な厳密モノイド関手が存在する。

これは具体的で強い結果ですが、もっとザックリ言えば：

幾何ブレイドの圏と組み合わせブレイドの圏は、モノイド圏として同値である。

幾何ブレイドの圏と組み合わせブレイドの圏は、モノイド圏としての構造からは区別できません。そして実際に、ほとんどの場合区別していません。

タングルの圏の公理的な特徴付け

モノイド圏にブレイド構造を入れたものとしてブレイド付きモノイド圏（braided monoidal category）があります。ブレイド付きモノイド圏の概念を使うと、ブレイドの圏は、単一の対象（1個の点）から生成されたブレイド付き厳密モノイド圏として特徴付けられます。別な言い方をすると、ブレイドの圏は「一番簡単なブレイド付きモノイド圏」です。

同様に、タングルの圏やその部分圏、変種の圏などを「一番簡単なナントカ圏」として特徴付けられないでしょうか？この問に答えるのはなかなかに面倒な話です。完成度の高い結果として、シャム（Mei Chee Shum*5）の定理をザッと紹介します。

原論文： http://www.sciencedirect.com/science/article/pii/002240499200039T

太さも幅も持たない紐の代わりに幅を持つ帯を使ったタングルを考えます。幅を持ったタングルを枠付きタングル（framed tangle）と呼びます。「枠」とは、向き付き曲線の接ベクトルと接ベクトルに直交する法ベクトル、接ベクトル×法ベクトルというベクトル積で作られる3次元座標系に起因します。ただし、向きも接ベクトルも考えなくても、枠付きタングルの圏を幅（区間との直積）だけで定義できます。パラメータ空間のあいだの同型や、方体のなかでのアンビエント・イソトピーを使って同値関係を入れるのも同じです。

一方、モノイド圏に構造を付けたものとしてリボン圏（ribbon category, a.k.a tortile category）があります。名前から、幅付き紐の公理化であろうと想像できます。シャムの定理は、この想像が当たりであることを教えてくれます。

単一の対象から生成されたリボン圏は、枠付きタングルの圏とモノイド圏として同値である。

これは、アルチンの定理の圏論的な発展形と捉えることができます。

もつれを整理すると

タングルやブレイドを素材とする圏、あるいはそれらを公理化した圏（の種別）はたくさんあります。

ブレイド付きモノイド圏（braided monoidal category）
対称モノイド圏（symmettric monoidal category）
トレース付きブレイド付きモノイド圏（traced braided monoidal category）
トレース付き対称モノイド圏（traced symmetric monoidal category）
バランス（ひねり）付きモノイド圏（blanced monoidal category）
自律圏（autonomous category）
旋回圏（pivotal category）
コンパクト閉圏（compact closed category）
リボン圏（ribbon category, tortile category）
...

あまりに色々ありすぎてウンザリします。

セリンガーがこれらを整理するレポートを書いています。

Title: A survey of graphical languages for monoidal categories (2009)
Author: Peter Selinger
Pages: 63p
URL: https://arxiv.org/abs/0908.3347

モノイド圏の博物学という感じもしますが、一種のモデル理論と捉えることができます。記号的な定義が構文論で、幾何的な定義が意味論です。アルチンの定理やシャムの定理は、構文的定義と意味的定義の一致を主張しているので完全性定理です。

この種の完全性定理は、“テキスト＝記号表現”と“絵＝幾何表現”の関係を示しています。テキストと絵の関係を調べることは、証明やコミュニケーションのスタイルを変革する基盤形成になるかも知れません。

「コミュニケーションの多次元化」という革命に立ち会っているのだと思う

*1:画像は http://missanga.seesaa.net/article/21655811.html より

*2:同相写像でも扱いが面倒なので、φ_tはH₀, H₁を動かさない、あるいはもっと強く、方体の境界は動かさないことにしてもいいです。

*3:アルチンの原論文（1946）がインターネット上にあります。http://www.maths.ed.ac.uk/~aar/papers/artinbraids.pdf 。同名（Theory of braids = Theorie der Zöpfe）のドイツ語論文は、それより20年も前の1926年に出ているようです。

*4:圏論版アルチンの定理をハッキリと述べたのはジョイアル／ストリート（Andre Joyal, Ross Street）らしいです。知っていた人はたくさんいるでしょうが。

*5:Mei-Chi Shum という表記もありますが、本人による表記はCheeです。ちなみにMei Chee Shumは女性で、現在は保険会社の幹部です。