圏のクリーネスター構成 -- エフイチに触発されて

下心モリモリでエフイチのお勉強をしている檜山です。はっきり言って、F₁の代数幾何／数論的な側面は僕にはサッパリわかりません。それでもエフイチ（F₁）が十分に興味深いのは、計算（computation）やソフトウェアの話のなかにもエフイチ現象が垣間見えるからです。存在するはずがない謎の“一元体”F₁の定式化のために、たくさんの人々が色んな道具を開発しています。それらの道具は本来の動機を超えて利用価値があるように思えます -- 代数幾何／数論とは関わりがない僕らにもね。

それと、F₁の物語にはいくつかの教訓が含まれているようです。

• あまりにも単純でヒドクつまらなそうなモノでも、想像を絶する深い構造を持つかもしれないぞ。
• まったく異なった分野・領域でも類似の現象があれば、それは偶然ではないかもしれない。
• ある体系内で欲しいモノが存在しないなら、その体系のほうを疑ってみる。
• 圏論使ってみ、うまくいくかもよ。
• 特にモノイド積（テンソル積）。

F₁の実体は、1だけからなる可換群（掛け算は、1×1 = 1 だけ）、またはそれにゼロを加えた {0, 1} だと見なされています*1。足し算さえないF₁を係数“体”とする線形代数を行ない、F₁を座標に使う幾何を展開し、F₁を物理量とする物理もできそうです。計算科学がこのオコボレにあずかってもいいんじゃないでしょうか。

直接的にF₁を使わなくても、エフイチ（F₁）っぽい発想で考えることはできます。対象が1個で恒等射しかない自明な圏Iについて考えているうちに、圏のクリーネスターを思いつきました。Cの非対称クリーネスターをC^#、対称クリーネスターをC^* とすると：

• I^# = N = (自然数の足し算を、モノイド積と考えたモノイド圏、結合は自明)
• I^* = S = (自然数nごとに、ホムセットS(n, n)を「n次対称群」としたモノイド圏)

圏のクリーネスターについてはこのエントリーで説明します。この構成法は簡単だし、特に新しくもないです。が、いろいろエフイチっぽく考えた副産物です。もとの圏Cが、データ型を対象として、型付きの逐次計算過程を射とする圏のとき、クリーネスターC^#, C^*は、Cの計算デバイスを使った並列計算の圏になります。

内容：

1. 圏の非対称クリーネスター
2. 自然数のタリー表現と自明圏の非対称クリーネスター
3. 圏の対称クリーネスター
4. アミダ図の圏と有限置換の圏
5. クリーネスター構成から派生するもの

圏の非対称クリーネスター

Cを圏として、Obj(C) = |C| と書き、射の集合Mor(C)を単にCとも書きます。対象は、a, b, cなど小文字で表記することにします -- A, B, C∈|C| なんて書いてしまうのを防ぐためです ^^;。Cⁿ = C×...×C (n個) は、普通にCの直積だとします。Cⁿの要素は、(f₁, ..., f₁)という長さnのタプルです。C⁰は空なタプル()だけからなる単元集合、C¹はCと同一視してもかまいません。

今作った C⁰, C¹, C², ... を全部直和で寄せ集めて、Dを作ります。

• D := C⁰ + C¹ + C² + ...

Dは自然に圏になります。Obj(D) = |D| は次のように定義します。

• |D| := |C|⁰ + |C|¹ + |C|² + ...

dom, cod, id, comp（結合、合成）は次のようですね。

1. dom[(f₁, ..., f_n)] = (dom[f₁], ..., dom[f_n])
2. cod[(f₁, ..., f_n)] = (cod[f₁], ..., cod[f_n])
3. id[(a₁, ..., a_n)] = (id[a₁], ..., id[a_n])
4. comp[(f₁, ..., f_n), (g₁, ..., g_n)] = (f₁, ..., f_n);(g₁, ..., g_n) = (comp[f₁, g₁], ..., comp[f_n, g_n])

Dは単に圏になるだけではなくて、(f₁, ..., f_n)□(g₁, ..., g_m) := (f₁, ..., f_n, g₁, ..., g_m) というタプルの連接によりモノイド圏になります。□はモノイド積（このケースでは連接）の演算記号、モノイド単位は長さ0のタプル()です。

演算が連接なので、Dの要素はタプルというよりは列（シーケンス、ストリング）と思ったほうがいいかもしれません。混乱の心配がなければ、(f₁, ..., f_n) を f₁ ... f_n のようなストリングで書いてもいいでしょう。空のタプル()は、丸括弧を取り除くとほんとに何もなくなりますが、形式言語理論の習慣に従ってεと書くと「空の存在」がはっきりします。

以上のように定義したDを、Cの非対称クリーネスターと呼び、D = C^# と書くことにします。

自然数のタリー表現と自明圏の非対称クリーネスター

はるかはるか昔、我々の祖先は、数の表現に棒とか紐とか札を使っていたでしょう。それらを模した短い線を、壁や板に刻んで数の表記（numeral）にしていたと思われます。この方式の数表現はタリー（tally）表現といいます。短い棒は、大文字Iを使うことにすると：

1. I -- イチ
2. II -- ニ
3. III -- サン

という具合。足し算は例えば：

• II + III = IIIII

何も書かないとゼロですが、εで「空の存在」を表すと、例えば：

• ε + III = III

さて、対象が1個、射も1個の圏（単位圏、自明圏）を考えます。対象の集合を{i}として、id_iをIと書きます。I;I = Iです。この圏をIとして、圏Iの非対称クリーネスターI^#を作ってみます。I^#の対象集合|I^#|は次の形をしています。（タプルの代わりにストリングを使っています。）

• {ε} + {i} + {ii} + {iii} + ... = {ε, i, ii, iii, ...}

射の集合も同様です。

• {ε} + {I} + {II} + {III} + ... = {ε, I, II, III, ...}

i, Iがn個並んだ記号的図形を iⁿ, Iⁿ とも書くとしましょう。圏としての構造は：

1. dom[Iⁿ] = iⁿ
2. cod[Iⁿ] = iⁿ
3. id[iⁿ] = Iⁿ
4. comp[Iⁿ, Iⁿ] = Iⁿ;Iⁿ = Iⁿ （その他は未定義）
5. Iⁿ□I^m = I^n+m （モノイド積）

この圏では、対象の集合Obj(I) = |I| と、射の集合 Mor(I) = I は同一視可能であり、そのとき、dom, cod, id は恒等写像のように見えます。また、圏の結合（composition）は事実上は無いようなもんです。生き残っている演算はモノイド積で、それが自然数の足し算を与えています。

圏の対称クリーネスター

圏Cの非対称クリーネスターC^#に射を付け足します。a, b∈|C| ごとに、σ_a,b:a□b→b□a という射を加えます。ただし、次のような法則を仮定します。（id_xを単にxと書いています。）

1. σ_a,b;σ_{b, a} = a□b
2. [σ_a,b□(c□d)];[(b□a)□σ_c,d] = [(a□b)□σ_c,d];[σ_a,b□(d□c)]
3. [σ_a,b□c];[b□σ_a,c];[σ_b,c□a] = [a□σ_b,c];[σ_a,c□b];[c□σ_a,b]

なんだか複雑そうですが、実はアミダ図に関する同値関係に過ぎません。（「アミダのクイズをErlangで解いてみるよ」参照。）

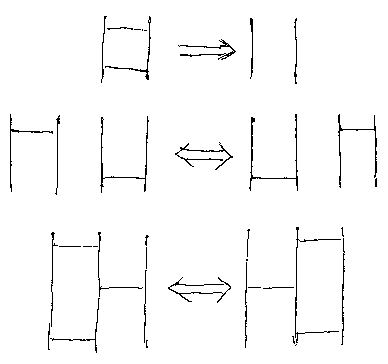
ブレイドの場合は、これらの関係式はアルチンの関係式です。結び目なら、一番目がライデマイスター移動II、三番目はライデマイスター移動IIIです。二番目は、モノイド圏の交替律を表現しています（スライディングとかシフティングと呼ばれることもあります）。ライデマイスター移動IIIは、ヤン・バクスター方程式とも呼ばれます。下の図は、ブレイドの場合のヤン・バクスター方程式です。今回は、ブレイドではなくてアミダなので、手前と奥の区別はありません。

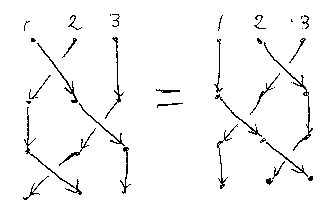
2つの対象の並びを交換するσを一般化したいときは、次のような関係式を使います（手前と奥の区別は無視）。

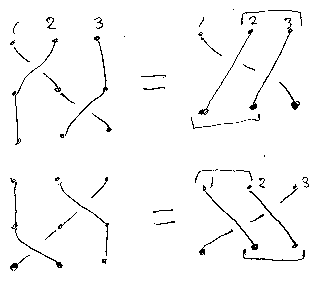
厳密な構成は多少面倒ですが、このようにσ達を足すと、対称モノイド圏ができます。出来上がった対称モノイド圏をC^*と書き、Cの対称クリーネスターと呼びましょう。C^*の対象の集合はC^#のそれと同じです。C^*の射の集合は、σ達を足した分だけC^#より増えています。

アミダ図の圏と有限置換の圏

アミダ図に、前節で登場したような同値関係（アルチン同値関係）を入れると、アミダが表すモノは、有限集合 {1, 2, ..., n} の自己全単射です。有限集合の自己全単射を置換（permutation）とも呼びます。また、置換を対称（symmetry）とも呼びます。圏Sは次のような圏だとしましょう。

1. |S| = {0, 1, 2, ...}
2. S(n, n) = (有限集合 {1, 2, ..., n} の置換の全体)
3. n≠m のとき、S(n, m) = 空
4. 射の結合は、置換の写像としての結合
5. 自然数の足し算を拡張してモノイド積を入れる。モノイド単位は0。

任意の置換が2つのモノの交換（互換；transposition）を繰り返せば得られることを利用すると、自明な圏Iから作った対称クリーネスターI^*がSと圏同値（より強く圏同型）であることが示せます。

圏Sは、アミダ図の圏にアルチン同値関係を入れて作ったモノですが、逆にアミダ図が置換（対称）の圏Sの図式的な表示を与えるとも言えます。

クリーネスター構成から派生するもの

この世で一番簡単な圏Iに非対称クリーネスター構成、対称クリーネスター構成をほどこすと、簡単ではありますが意味のある構造が出てきました。I^#と同型なモノイドNは、子供達が最初に習う計算の世界です。I^*と同型な圏Sに部分性（partiality）を入れると、ハランの圏Fが出てきます。ハランの圏Fは、一元体F₁の圏論的な対応物でした。

もとになる圏Cの射がなんらかの意味で計算プロセスとみなせるなら、C^#の射は独立して（相互作用なしで）動作する並列計算プロセスの圏となります。C^*では、値または状態のスワップを許します。Cが可逆計算の圏（亜群）なら、C^#もC^*もやはり可逆計算の圏です。

クリーネスターは形式言語理論に由来しますが、クリーネスターを与える式の形 1 + X + X² + ... を見ると、テンソル代数の構成と同じことがわかります。物理のフォック空間（Fock space）も同じ形です。線形論理の線形モダリティ（linear modality）の構成にもこの形を使います。1 + X + X² + ... が、ベキ等な世界における指数関数のテーラー展開である状況証拠がいくつかあります。

最初に挙げた教訓「まったく異なった分野・領域でも類似の現象があれば、それは偶然ではないかもしれない」によれば、これらの類似は偶然ではなく、なにかの必然かもしれません。

*1:F₁を集合論的な構造として見てもしょうがなくて、世界を下支えするナニモノカとしての役割が重要です。世界の見え方を規定している原理といってもいいでしょう。F₁より基本的な原理はないと思われているので、もはや相対化できない絶対的な原理です。